天平难题——UVa 1354

题目描述

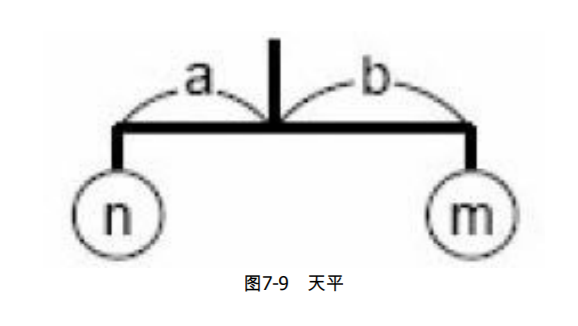
给出房间的宽度r和s个挂坠的重量wi。设计一个尽量宽（但宽度不能超过房间宽度r）的天平，挂着所有挂坠。天平由一些长度为1的木棍组成。木棍的每一端要么挂一个挂坠，要么挂另外一个木
棍。如图7-9所示，设n和m分别是两端挂的总重量，要让天平平衡，必须满足\(na=mb\)。

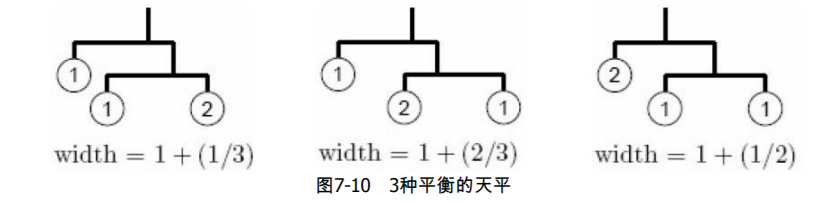
例如，如果有3个重量分别为1, 1, 2的挂坠，有3种平衡的天平，如图7-10所示

挂坠的宽度忽略不计，且不同的子天平可以相互重叠。如图7-11所示，宽度为(1/3)+1+(1/4)。

输入第一行为数据组数。每组数据前两行为房间宽度r和挂坠数目\(s（0<r<10，1≤s≤6）\)。以下s行每行为一个挂坠的重量\(W_i（1≤wi≤1000）\)。输入保证不存在天平的宽度恰好在\(r^{-10-5}\)和\(r^{+10-5}\)之间（这样可以保证不会出现精度问题）。对于每组数据，输出最优天平的宽度。如果无解，输出-1。你的输出和标准答案的绝对误差不应超过\(10^{-8}\)。

输入输出示例

Sample Input
5
1.3
3
1
2
1
1.4
3
1
2
1
2.0
3
1
2
1
1.59
4
2
1
1
3
1.7143
4
1
2
3
5

Sample Output
-1
1.3333333333333335
1.6666666666666667
1.5833333333333335
1.7142857142857142

思路

思路不难想，一个天平可以用一个二叉树来表示，只需要枚举所有的二叉树组合然后计算总宽度，取在房间宽度范围内最大的即可。

用一个数组保存所有节点，当选中i,j时，需要合并i和j为一个新的二叉树，我们这里选择了从i向j合并，就是合并完的节点在j位置。

l[i]代表第i个节点位置的左边总长度，r[i]代表右边总长度，w[i]代表重量。

有些地方可以应用回溯思想，减少多余的递归分支。

难想的地方是天平可能出现覆盖，有的天平可能完全不为总宽度贡献一点宽度，有的应该出现在右侧的天平可能为左侧贡献宽度，大概就是这样。

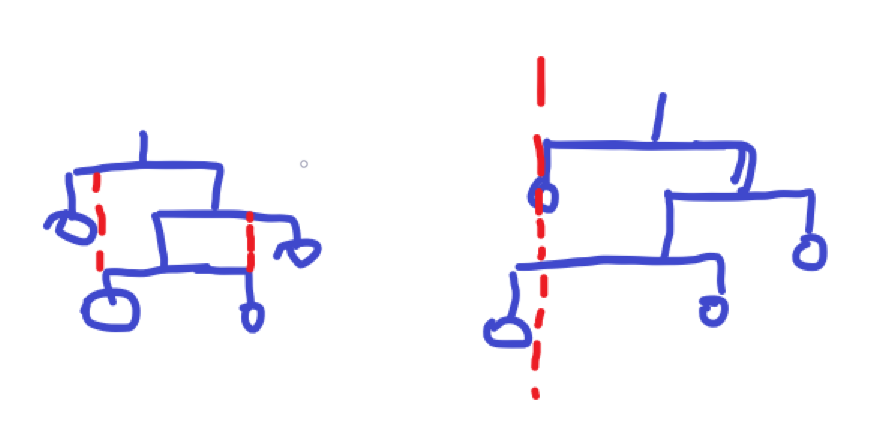
第一种情况其实还好，自底向上直接构造可以避开，第二种情况是我们需要考虑清楚的。

简而言之，我们需要再左侧的长度和右子节点的左侧长度中选一个最大的出来作为总左侧长度。也就是说对于节点i，你不仅要计算\(l[i]+a\)，你还要算\(-b+l[r[i]]\)。（a和b为木棍的左右长度）。而反过来也是一样的。

代码

#include "iostream"
#include "cstdio"
#include <algorithm>
#include "cstring"

#define MAXN 8

using namespace std;

double W, w[MAXN], ans, l[MAXN], r[MAXN];
int n, vis[MAXN];

void dfs(int cur) {
    if (cur == n) {
        for (int i = 1; i <= n; i++) {
            if (vis[i])continue;
            if (l[i] + r[i] > W)continue;
            ans = max(ans, l[i] + r[i]);
        }
        return;
    }
    for (int i = 1; i <= n; i++) {
        if (vis[i])continue;
        for (int j = 1; j <= n; j++) {
            if (i == j || vis[j])continue;
            vis[i] = 1;
            double a = w[j] / (w[i] + w[j]), b = 1 - a;
            w[j] += w[i];
            double tmpl = l[j], tmpr = r[j];
            l[j] = max(l[i] + a, -b + l[j]); 
            r[j] = max(r[j] + b, -a + r[i]);
            dfs(cur + 1);
            vis[i] = 0;
            w[j] -= w[i];
            l[j] = tmpl;
            r[j] = tmpr;
        }
    }
}

int main() {
    int t;
    scanf("%d", &t);
    for (int i = 0; i < t; i++) {
        memset(vis, 0, sizeof(vis));
        memset(l, 0, sizeof(l));
        memset(r, 0, sizeof(r));
        ans = -1;
        scanf("%lf %d", &W, &n);
        for (int i = 1; i <= n; i++)
            scanf("%d", &w[i]);
        dfs(1);
        printf("%.16lf\n", ans);
    }
    return 0;
}

天平难题——UVa 1354

原文：https://www.cnblogs.com/lilpig/p/14073925.html