数据结构绪论

1.什么是数据结构

数据结构是计算机中存储、组织数据的方式。通常情况下，精心选择的数据结构可以带来最优效率的算法。——《中文维基百科》
数据结构是相互之间存在的一种或多种特定关系的数据元素的集合。——《数据结构（清华大学出版社）》

数据结构的形式定义：一个二元组
Data_Structure = (D,S) 其中：D是数据元素的有限集，S是D上关系的有限集。
注意：解决问题的方法效率，跟数据的组织方式有关。
注意：解决问题的方法效率，跟算法的巧妙程度有关。

2.基本概念和术语

• 数据（data）:是对客观事物的符号表示，在计算机科学中是指所有能够输入到计算机中并被计算机程序处理的符号的总称，不仅仅包括整形、实型等数值类型，还包括字符及声音、图像、视频等非数值类型。
• 数据元素（data element）:是数据的基本单位，在计算机程序中通常作为一个整体进行考虑和处理。如畜类牛、马、羊、鸡、猪、狗等动物当然就是畜类的数据元素。
• 数据对象（data object）：是性质相同的数据元素的集合，是数据的一个子集。（指数据元素具有相同数量和类型的数据项，如人类这个例子，都有姓名、生日、性别等相同的数据项。）
• 数据项（data item）：一个数据元素可以由若干个数据项组成（如人类这个例子，都有姓名、生日、性别等相同的数据项）。
• 逻辑结构：结构中定义的关系描述的是数据元素之间的逻辑关系，称为逻辑结构。
• 物理结构：数据结构在计算机中的表示（又称为映像）称为数据的物理结构，又称为存储结构。
• 数据结构的分类：根据数据元素之间关系的不同特性，通常有下列四类基本结构：

1. 集合 结构中的数据元素之间除了同属于一个集合的关系别无其他关系。
2. 线性结构 结构中的数据元素之间存在一个对一个的关系。
3. 树形结构 结构中的数据元素之间存在一个对多个的关系。
4. 图状结构/网状结构 结构中的数据元素之间存在多个对多个的关系。

• 拓展:在计算机中表示信息的最小单位是二进制数的一位,叫做位（bit）；在计算机中我们使用一个由若干位组合起来形成的一个位串表示一个数据元素（如用8位二进制数表示一个字符）,通常称这个位串为元素或者结点。当数据元素由若干数据项组成时，位串中对应与各个数据项的子位串称为数据域。因此，元素或者结点可看成是数据元素在计算机中的映像。
  根据图片加深基本概念理解：）
  

• 数据元素之间的关系在计算机中有两种不同的表示方法：顺序映像和非顺序映像，并由此得到两种不同的存储结构：顺序存储结构和链式存储结构。
  顺序映像特点：借助元素在存储器中的相对位置来表示数据元素之间的逻辑关系；
  非顺序映像特点：借助只是元素存储地址的指针（pointer）表示数据元素之间的逻辑关系。
  注意：数据的逻辑结构和物理结构是密切相关的两个方面，任何一个算法的设计取决于选定的数据（逻辑）结构，而算法的实现依赖于采用的存储结构。

• 数据类型（data type）：与数据结构密切相关的一个概念，指一个值的集合和定义在这个值集上的一组操作的总称。（例如：C语言中的整型变量，其值集为某个区间上的整数，定义在其上的操作为加、减、乘、除和取模等算数运算）

• 抽象数据类型（Abstract Data Type简称ADT）：指一个数学模型以及定义在该模型上的一组操作。抽象数据类型的定义仅取决于它的一组逻辑特性，而与其在计算机内部如何表示和实现无关，即不论其内部结构如何改变，只要它的数学特性不变，都不影响其外部的使用。

• 拓展：抽象数据类型和数据类型实际上是一个概念。例如：各个计算机都拥有的“整数”类型是一个抽象数据类型，尽管它们在不同处理器上实现的方法不同，但是由于定义的数学特性相同，在用户看来都是相同的。因此，“抽象”的意义在于数据类型的数学抽象特性。

• 抽象数据类型按照其值的不同特性可分为三种：

• 原子类型

• 固定聚合类型

• 可变聚合类型
  显然，后两种可称为结构类型。

• 抽象数据类型可用三元组表示：（D,S,P）
  其中，D是数据对象，S是D上的关系集，P是对D的基本操作集。
  例：

ADT Triplet{
数据对象：D={e1,e2,e3|e1,e2,e3属于ElemSet(定义了关系运算的某个集合)
数据关系;R1={<e1,e2>,<e2,e3>}
基本操作：
InitTriplet(&t,v1,v2,v3)
操作结果：构造了三元组T,元素e1,e2和e3分别被赋以参数v1,v2和v3的值。
DestroyTriplet(&T)
操作结果：三元组T被销毁
Get（T,i，&e）
初始条件：三元组T已存在，1<=i<=3
操作结果：用e返回T的第i元的值
put（&T，i，e,）
初始条件：三元组T已存在，1<=i<=3
操作结果：改变T的第i元的值为e
IsAscending(T)
初始条件：三元组T已存在
操作结果：如果T的3个元素按升序排列，则返回1，否则返回0
IsDescending(T)
初始条件：三元组T已存在。
操作结果：如果T的3个元素按降序排列，则返回1，否则返回0.
Max（T，&e）
初始条件：三元组T已存在
操作结果：用e返回T的三个元素中的最大值
Min（T，&e）
初始条件：三元组T已存在
操作结果：用e返回T的三个元素中的最小值
}ADT Triplet

3.算法和算法分析

1. 算法（Algorithm）定义:是对特定问题求解步骤的一种描述，是指令的有限序列。

• 有穷性：一个算法必须总是在执行有限的步骤之后结束，并且每一步都必须在有限的时间内完成。
• 确定性：算法中每一条指令必须有确切的含义，读者理解时不会产生二义性。并且在任何条件下，算法只有唯一的一条路径，即对于相同的输入只能得出相同的输出。
• 可行性：一个算法是能行的，即算法中描述的操作是可以通过已经实现的基本运算执行有限次来实现的。
• 输入：一个算法有零个或多个输入，这些输入取决于某个特定对象的集合。
• 输出：一个算法有一个或多个输出，这些输出是同输入有着某些特定关系的量。
  例：
  选择排序的伪码算法描述

void SelectionSort(int List[],int N)
{/*将N个整数List[0]...List[N-1]进行非递减排序*/
      for(int i = 0;i < N,i++){
            MinPosition = ScanForMin(List,i,N-1);
            /*从List[i]到List[N-1]中找最小元，并将其位置赋给MinPosition*/
            Swap(List[i],List[MinPosition]);
            /*将未排序部分的最小元换到有序部分的最后位置*/
      }
}

• 算法设计的要求（一个好的算法应考虑的因素）：

1. 正确性：算法应当满足具体问题的需求。
2. 可读性：算法主要是为了人的阅读和交流，其次才是及机器执行。
3. 健壮性：当输入非法数据时，算法能够适当做出反应并进行处理，不会产生莫名其妙的结果。
4. 效率与低存储量需求：通俗地讲，效率指的是算法执行时间，存储量指的是算法执行过程中所需要的最大存储空间。（时间复杂度T(n)和空间复杂度S(n)）

• 算法效率的度量（事后统计与事前分析估算法）：一个算法是由控制结构（顺序、分支、循环3种）和原操作（指固有数据类型的操作）构成的，算法时间取决于两者的综合效果。一般为了便于比较同一问题的不同算法，通常做法是从算法中选取一种对于所研究的问题（或者算法类型）来说是基本操作的原操作，以该基本操作重复执行的次数作为算法的时间度量。
  例：在如下所示的两个NXN矩阵相乘的算法中，“乘法”运算是“矩阵相乘问题”的基本操作。整个算法的执行时间与该基本操作（乘法）重复执行的次数n^3成正比，记作T(n)=O(n^3)。

for(i = 1;i <= n,++i){
      for(j = 1;j <=n;++j){
            c[i][j] = 0;
            for(k = 1;k <= n;++k)
                  c[i][j] += a[i][k]*b[k][j];
      }
}

• 复杂度函数图像表示：
  

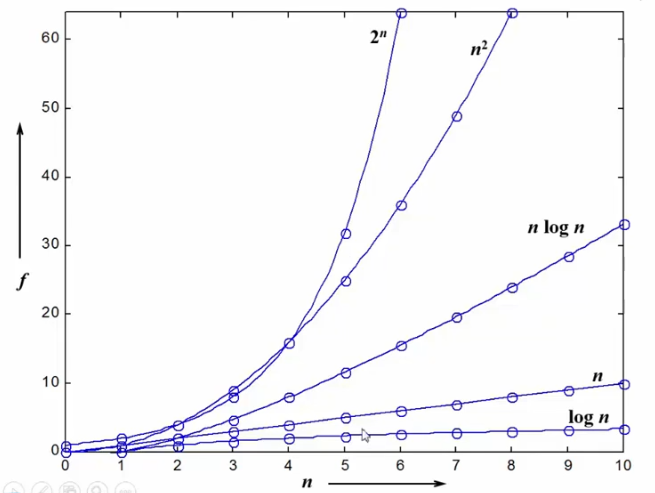
• 复杂度分析技巧：

1. 若两段算法分别有复杂度T1(n)=O(f1(n))和T2(n)=O(f2(n)),则
   T1(n)+T2(n)=max(O(f1(n)),O(f2(n)))
   T1(n)xT2(n)=O(f1(n)xf2(n))
2. 若T(n)是关于n的k阶多项式，那么T(n)=θ(n^k)。
3. 一个for循环的时间复杂度等于循环次数乘以循环体代码的复杂度。
4. if-else结构的复杂度取决于if的条件判断复杂度和两个分支部分的复杂度，总体复杂度取三者中最大。

应用实例：
给定N个整数序列{A1，A2...AN},求函数f(i,j),f(i,j)是指该序列中和最大的子序列之和。
算法1：

int MaxSubseqSum1(int A[],int N)
{ int ThisSum,MaxSun = 0;
  int i,j,k;
  for(i = 0;i < N；i++){/*i是子列左端位置元素*/
    for(j = i;j < N;j++){/*j是子列右端位置元素*/
      ThisSum = 0;/*ThisSum是从A[i]到A[j]的子列和*/
      for(k = i;k <= j;k++)  
        ThisSum += A[k];
      if(ThisSum > MaxSum)/*判断刚得到的子列和是否更大*/
        MaxSum = ThisSum;/*如果条件成立，则更新结果*/
    }/*j循环结束*/
  }/*i循环结束*/
  return MaxSum;
}

不难分析，有三重嵌套循环，故T(n)=O(N^3);
算法2：

int MaxSubseqSum1(int A[],int N)
{ int ThisSum,MaxSun = 0;
  int i,j;
  for(i = 0;i < N；i++){/*i是子列左端位置元素*/
    ThisSum = 0;/*ThisSum是从A[i]到A[j]的子列和*/
      for(j = i;j < N;j++){/*j是子列右端位置元素*/
        ThisSum += A[j];
        /*对于相同的i,不同的j，只要在j-1次循环的基础上累加一项即可*/
      if(ThisSum > MaxSum)/*判断刚得到的子列和是否更大*/
        MaxSum = ThisSum;/*如果条件成立，则更新结果*/
    }/*j循环结束*/
  }/*i循环结束*/
  return MaxSum;
}

算法2在算法1基础上进行改进，T(n)=O(N^2);
算法3：分而治之

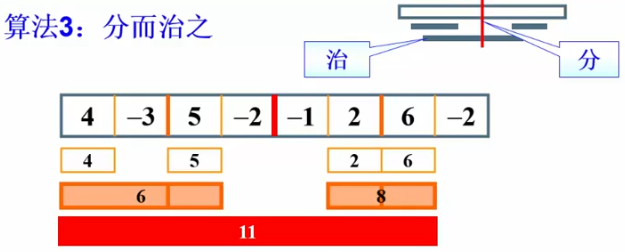
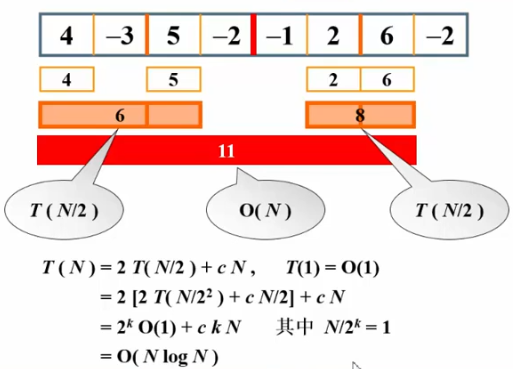
算法4：在线处理（在线的意思是指每输入一个数据就进行即时处理，在任何一个地方终止输入，算法都能够正确给出当前解）

int MaxSubseqSum4(int A[],int N)
{ int ThisSum,MaxSum;
  int i;
  ThisSum = MaxSum = 0;
  for(i = 0;i < N;i++){
    ThisSum += A[i];/*向右累加*/
    if(ThisSum > MaxSum)
      MaxSum = ThisSum;/*发现更大子列和则更新当前结果*/
    else if(ThisSum < 0)/*如果当前子列和为负*/
      ThisSum = 0;/*则不可能使后面的部分和增大，抛弃之*/*********************重点************************
  }
  return MaxSum;
}

其算法复杂度为T(n)=O(N)(最快的算法）。

1.数据结构绪论

原文：https://www.cnblogs.com/masterYHH/p/14079073.html