Lcez#111 yist

原题题面

Description

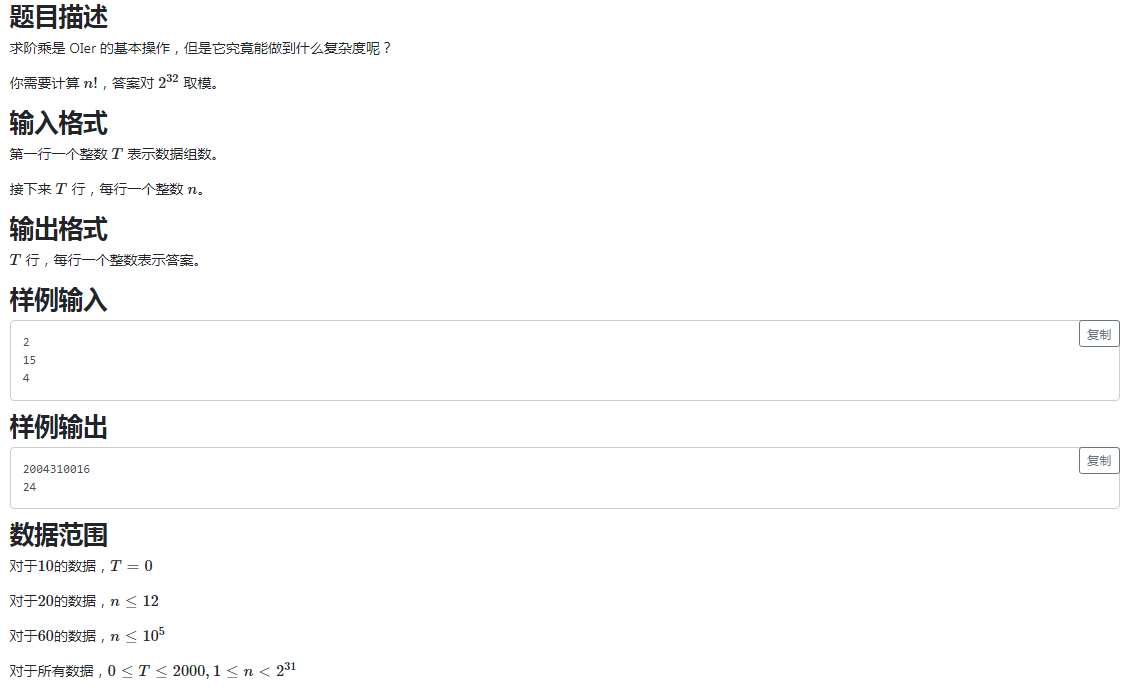
给定 \(n\)，求 \(n!\ \%\ 2^{32}\)

Solution

60pts

暴力。

Code

#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
const ll Mod=4294967296;
inline ll f(ll x){
	ll res=1;
	for(ll i=1;i<=x;i++) res=res*i%Mod;
	return res%Mod;
}
int main(){
	//freopen("out.txt","w",stdout);
	int t;
	ll n;
	scanf("%d",&t);
	for(int i=1;i<=t;i++){
		scanf("%lld",&n);
		printf("%lld\n",f(n)%Mod);
	}
	return 0;
}

100pts

显然，不能得到 100pts 的原因是 \(f\) 函数耗时太久。

考虑如何优化。

优化不难想到针对模数（\(2^{32}\)）进行优化。

用 60pts 的代码先打一个表尝试推一推结论 / 规律。

可以打出这样的表。

不难发现，在 2147483648 后，即 \(2^{31}\) 之后，结果全部为 0 。

所以在 \(f\) 函数中加一句特判，即可大大降低时间复杂度。

inline ll f(ll x){
	ll res=1;
	for(ll i=1;i<=x;i++){
		if(res*i%Mod==0) return 0;
		res=res*i%Mod;
	}
	return res%Mod;
}

Code

#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
const ll Mod=4294967296;
inline ll f(ll x){
	ll res=1;
	for(ll i=1;i<=x;i++){
		if(res*i%Mod==0) return 0;
		res=res*i%Mod;
	}
	return res%Mod;
}
int main(){
	//freopen("in.txt","r",stdin);
	//freopen("out.txt","w",stdout);
	int t;
	ll n;
	scanf("%d",&t);
	for(int i=1;i<=t;i++){
		scanf("%lld",&n);
		printf("%lld\n",f(n)%Mod);
	}
	return 0;
}

Lcez#111 yist

原文：https://www.cnblogs.com/-pwl/p/14082552.html