上篇博客我们说到了线性表,线性表有一个巨大的缺点,就是我们需要提前知道元素的数据量,并且在使用线性表时,必须要考虑到数据量的变化,从而分配合适大小的内存来保存这些数据,线性表还有一个很大的缺点就是在增加、删除表中的元素时,需要频繁地移动元素,以达到线性存储的标准。
链表的存在就是为了解决这些问题的,链表的每一个节点都存储在不同的内存空间中,每一个节点都包含了指向了下一个节点的指针,以此达到线性存储的目的,链表其实是线性表的另一种实现方式。
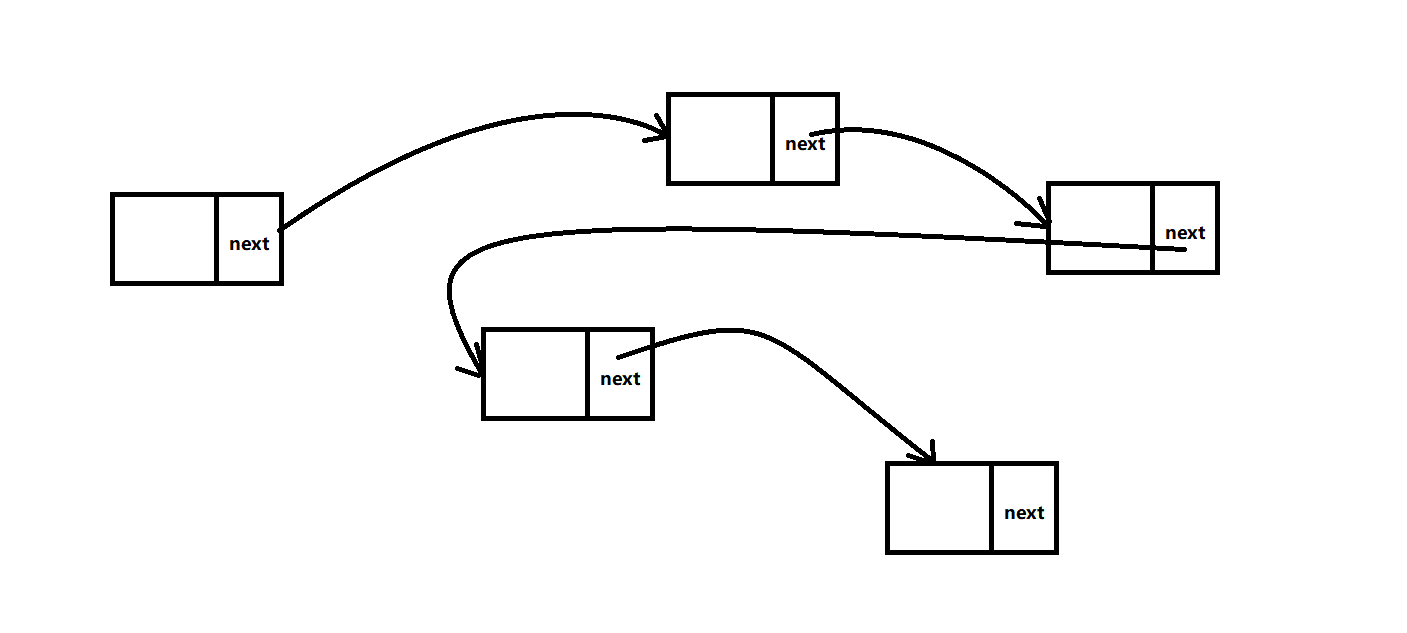
注意:这是链表的概念图,并不是所有的链表都是这个样子的
在我们使用链表时,我们通常会把链表的第一个节点空出来,来表示这是特殊的节点,也就是链表的头部,我们将其称之为头节点,头节点的存在是为了更方便地操作整个链表。
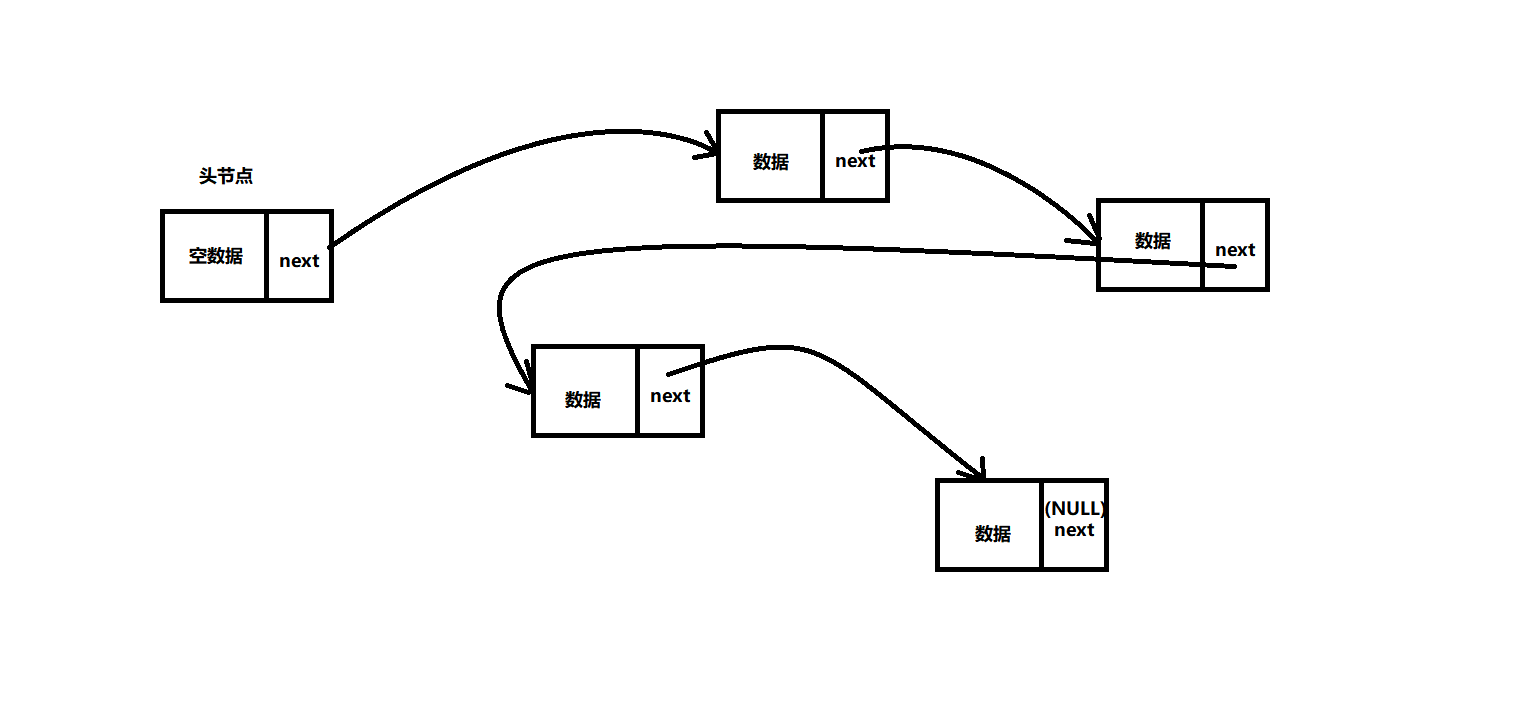
注意:这是链表的概念图,并不是所有的链表都是这个样子的
注意:头节点并不是链表必须的。
头指针是指向链表第一个元素的指针,如果链表中包含头节点,那么头指针就指向头节点。
头指针具有标识的作用,我们常用头指针的名称来表示整个链表。
不论链表是否为空,头指针均不为空,头指针是链表的必要元素。
先引入我们需要使用到的头文件:
#include <stdio.h>
#include <stdlib.h>
//这里我想使用time来生成一些随机数,模拟数据的存储
#include <time.h>
然后定义我们需要用到的数据:
#define OK 1
#define ERROR 0
//这个是结点的数据类型,我这里使用了int
typedef int ElemType;
typedef int Status;
定义节点:
typedef struct Node
{
ElemType data;
//这个是指向下一个节点的指针
struct Node *next;
}Node;
//声明LinkList
typedef struct Node *LinkList;
使用这样的存储结构我们的操作很自由,我们可以选择在链表的头部进行插入,这样的话,每次新增一个元素我们就不用关心链表中其它节点,只需要让每个新增的节点都呆在头节点的后边就可以了。
//LinkList*是指向链表的指针(头指针),n表示我们要创建的链表长度
void CreateListHeader(LinkList *L, int n)
{
LinkList p; //节点
int i;
srand(time(0)); //设置随机数种子
*L = (LinkList)malloc(sizeof(Node)); //创建一个头节点
(*L)->next = NULL;
for(i = 0;i < n;i++)
{
p = (LinkList)malloc(sizeof(Node));
p->data = rand() % 100 + 1; //取0 - 100
//新的节点指向头节点所指向的节点
p->next = (*L)->next; //如果此时只包含一个头节点,新的节点将指向空
(*L)->next = p; //头节点指向新的节点
}
}
还有一种做法就是,将每次新增的节点都存放在链表的最后边:
void CreateListTail(LinkList *L, int n)
{
LinkList p, r;
int i;
*L = (LinkList)malloc(sizeof(Node));
//头节点无指向
(*L)->next = NULL;
r = *L; //r此时就是头节点
for(i = 0;i < n;i++)
{
p = (LinkList)malloc(sizeof(Node));
p->data = rand() % 100 + 1;
r->next = p; //r控制当前节点指向下一个节点,也就是p(新增的节点)
r = p; //r指向p
}
//最后一个节点指针为空
r->next = NULL;
}
//L是头节点,i是要查询的元素位置,e是我们在方法正常执行完成后要返回的值
Status GetElem(LinkList L, int i, ElemType *e)
{
int j = 1;
LinkList p;
p = L->next; //执行完此步操作之后,p是第一个节点
while(p && j < i)
{
p = p->next;
++j;
}
if(j != i || !p)
return ERROR;
*e = p->data;
return OK;
}
//i是指定要插入到链表的哪个位置
Status ListInsert(LinkList *L, int i, ElemType e)
{
LinkList p, s;
int j = 1;
p = *L;
while(p && j < i)
{
p = p->next;
++j;
}
if(j != i || !p)
return ERROR;
s = (LinkList)malloc(sizeof(Node));
s->data = e;
s->next = p->next;
p->next = s;
return OK;
}
Status ElemDetele(LinkList *L, int i, ElemType *e)
{
LinkList p, q;
int j = 1;
p = *L; //此时p为头节点
//注意这里是p->next
while(p->next && j < i)
{
//第一次p->next其实是指向的头节点
p = p->next;
++j;
}
//如果遍历是我们预期的那样,那么p->next应该是第i个元素
//因为我们其实在操作链表时,要遍历到的其实是第i个结点的上一个节点(不要忽略头节点的存在哦)
if(j != i || !(p->next))
return ERROR;
//q此时就是要被删除的节点
q = p->next;
p->next = q->next; //如果要删除的节点是最后一个节点,那么此时q->next应该是NULL
*e = q->data; //取出要删除的节点的数据
free(q); //删除节点
return OK;
}
Status ClearList(LinkList *L)
{
LinkList p, q;
p = (*L)->next; //p指向了第一个节点
while(p)
{
q = p->next;
free(p);
p = q;
}
(*L)->next = NULL; //清除了除头节点以外的所有节点
return OK;
}
Status ErgodicList(LinkList L)
{
//如果链表为空就返回错误
if (!L)
return ERROR;
LinkList p;
//p此时为第一个节点(L是第一个节点,也就是头节点,所以L->next取出的是第一个有效节点)
p = L->next;
//判断当前节点是否为空
while (p)
{
//打印节点中的数据
printf("%d\t", p->data);
//p为下一个节点
p = p->next;
}
printf("\n");
return OK;
}
这里我给出了简单的测试方法(其实返回的ERROR等信息,这里没有用到,我这么做是为了更清楚地演示链表逻辑):
int main()
{
//初始化头指针
LinkList L = NULL;
CreateListHeader(&L, 10);
ErgodicList(L);
printf("增加节点到最后一个位置\n");
LinkInsert(&L, 11, 20);
ErgodicList(L);
int remove = 10;
printf("\n删除第%d个节点:", remove);
ElemType e = 0;
LinkDelete(&L, remove, &e);
printf("\n第三个节点是%d", e);
printf("\n移除%d个节点之后,链表的结构:",remove);
ErgodicList(L);
printf("清空链表,链表数据:\n");
ClearList(&L);
ErgodicList(L);
return 0;
}
该博客总结于书籍:大话数据结构 --很简单易懂的算法与数据结构的书
原文:https://www.cnblogs.com/erosion2020/p/14088537.html