以下讨论的场景的前提都包括:给定一个正向排序的数组vector<int> nums和给定需要求取的目标值target,来进行讨论。
因为二分查找的目标是确定某个具体下标,所以每次取中值mid后,只要其对应的数值与target相等就可以进行函数的返回。如果在循环退出后,仍然没有查找到确定值,就可以判定未不存在合理解。
因此我们考虑使用闭口区间进行while循环的筛选,当mid值不等于target时,左边界变动未left = mid + 1,右边界变动为right = mid - 1。while(left <= right)循环退出的条件即为left = right - 1。
基本框架如下:
// 给定vector数组
// 给定目标值
vector<int> nums{ ... };
int target;
int left = 0;
// right边界初始化为末尾元素
int right = nums.size() - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] > target)
right = mid - 1;
}
// 二分查找目标失败
return -1;
而搜寻左边界我们使用的循环终止条件是半开半闭区间。其大致框架如下:
// 给定vector数组
// 给定目标值
vector<int> nums{ ... };
int target;
int left = 0;
// right边界初始化为数组长度
int right = nums.size();
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target)
right = mid;
else if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] > target)
right = mid;
}
与具体下标的代码框架有所不同,重点在于对于nums[mid] == target的处理。
if (nums[mid] == target)
right = mid;
当找到目标值并没有立刻退出循环返回下标,而是缩小搜索区间的上界right,在区间[left, mid)中继续搜索,不断向左收缩,达到锁定左侧边界的目的。
并且同时右边界也没有向之前一样修改为right = mid - 1,而是:
if (nums[mid] > target)
right = mid;
造成右边界变换方式改变的原因,主要是搜索区间由闭区间转变成左闭右开区间的缘故:
[left, right]讨论完mid后,下一步搜索空间去掉mid并分割成[left, mid-1]和[mid+1, right]mid后,剩下的区间应该按照循环条件的格式分割成分割成[left, mid)和[mid+1, right)。另外,关于右边界初始化的细节:
int left = 0, right = nums.size();
不同于求具体下标的题目,将右边界初始为right = nums.size()-1,即末位数组元素。其实也是跟搜索区间有关:
[lef, right],如果取数组长度为下标回越界出错。[left, right),右侧开区间取不到,可以尝试此类型的初始化。循环退出的条件为left == right,所以函数只会在退出循环后进行函数值的返回。我们需要对返回的left或者right进行讨论和筛选,错误的情况直接返回-1。
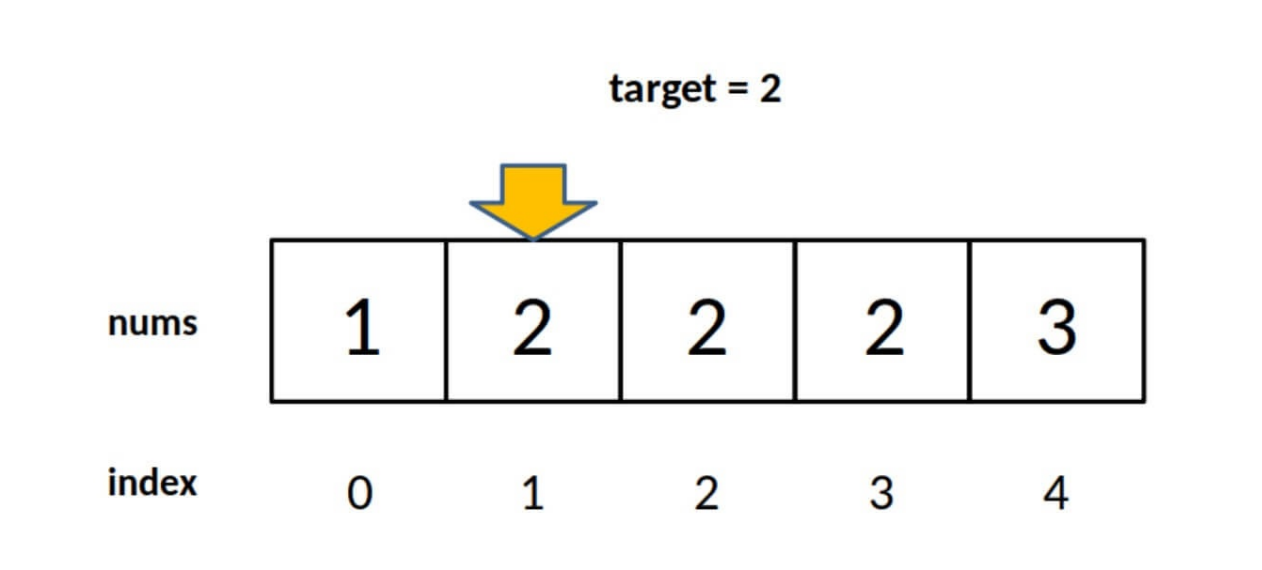
对于上图的情况,该算法回返回1。可以理解成nums中小于2的元素有1个。
对于target小于有序数组所有元素的情况,比如对于有序数组 nums = [2,3,5,7] , target = 1 ,算法会返回 0,含义 是:nums 中?于 1 的元素有 0 个。
对于target大于有序数组所有元素的情况,比如说 nums = [2,3,5,7], target = 8 ,算法会返回 4,含义是: nums 中?于 8 的元素有 4 个。
因此对于循坏外的筛选代码如下:
if (left == nums.size()) return -1;
if (nums[left] != target) return -1;
return left;
通过上述讨论,我们知道退出循环后left可能有以下几种情况:为0也可能为nums.size():
left == 0,说明数组中没有比target小的元素。但同时我们也要筛选掉目标值target就在下标为0的情况,所以我们需要对下标left处的元素值进行筛选。if (nums[left] != target),那么二分查找就是失败的,否则函数就返回下标值。left == nums.size(),说明数组中没有比target大的元素。二分查找失败,如果不经过此步骤讨论直接进行left下标对应元素值的判断,可能回出现数组越界的段错误,所以上述两句筛选缺一不可,并且代码顺序也不可更改。与查询左边界类似,代码框架如下:
// 给定vector数组
// 给定目标值
vector<int> nums{ ... };
int target;
int left = 0;
// right边界初始化为数组长度
int right = nums.size();
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target)
left = mid + 1;
else if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] > target)
right = mid;
}
类似地,关键点还是在这里:
if (nums[mid] == target)
left = mid + 1;
当nums[mid] == target时不要立即返回,而是增大搜索区间的下界left,使得区间不断向右收缩,达到锁定右侧边界的目的。
同样,对于循环终止时的left == right,我们也要进行筛选,对于二分查找失败的情况返回-1。
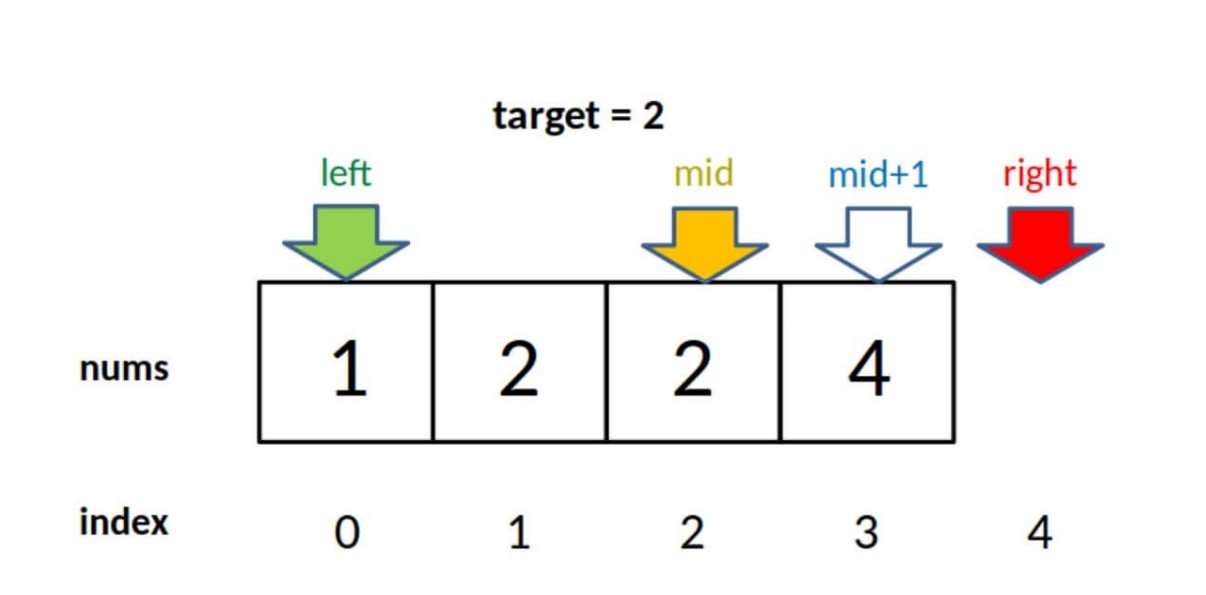
对于上图的情况,该算法回返回3。可以理解成nums中小于等于target2的元素有3个。
对于target小于有序数组所有元素的情况,比如对于有序数组 nums = [2,3,5,7] , target = 1 ,算法会返回 0,含义 是:nums 中?于等于 target1 的元素有 0 个。
对于target大于有序数组所有元素的情况,比如说 nums = [2,3,5,7], target = 8 ,算法会返回 4,含义是: nums 中小于等于target 8 的元素有 4 个。
if (left == 0) return -1;
if (nums[left - 1] != target) return -1;
return left - 1;
不要跟左边界的区别弄混,虽然两者都涉及到0下标和数组长度下标的讨论。由于我们对于下标nums的理解,查找左边界时,确定的下标时target的首位元素位置,而查找右边界时,确定的下标是末位target元素位置的后一位!!!。因此对于查找右边界的情况,如果返回的下标是0,可以肯定二分查找失败了。而取右边界时,返回下标前的值是小于等于target的,所以需要讨论前一位nums[left - 1]的值是否等于target。
统计一个数字在排序数组中出现的次数。
示例 1:
输入: nums = [5,7,7,8,8,10], target = 8
输出: 2
示例 2:
输入: nums = [5,7,7,8,8,10], target = 6
输出: 0
限制:
class Solution {
public:
int search(vector<int>& nums, int target) {
// 先寻找左边界
int left = 0, right = nums.size();
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target)
right = mid;
else if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] > target)
right = mid;
}
// 两种筛选缺一不可
// 筛选不存在目标元素的情况
if (left == nums.size()) return 0;
// 筛选左右指针重合到0位置,但映射元素不为目标元素的情况
if (nums[left] != target) return 0;
// 开区间寻找左边界是可取的目标值
// 开区间寻找有边界是不可取的非目标值
int leftBorder = left;
right = nums.size();
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target)
left = mid + 1;
else if (nums[mid] < target)
left = mid + 1;
else if (nums[mid] > target)
right = mid;
}
int rightBorder = left;
return (rightBorder - leftBorder);
}
};
浅谈二分查找框架+剑指 Offer 53 - I (C++)
原文:https://www.cnblogs.com/buryinshadow/p/14117360.html