2011年,Hinton发表了Transforming Auto-Encoder,介绍的就是胶囊网络。一个胶囊就是一组神经元,你可以将其类比成一个神经元。常规的神经元,输入的是很多个标量,输出是一个标量。而胶囊的输入是很多向量,输出是一个向量,这个向量称作胶囊的激活向量。这个激活向量是该胶囊所识别的一类实体的实例化参数,实体可以是一个物体,也可以是一个物体的一个部分。激活向量的长度(向量的模)代表了这个实体激活这个胶囊的概率,或者说这个胶囊能识别某种模式的概率。本文的重点是介绍一个动态路由算法,该算法详细地定义了两层胶囊网络之间的前向传播过程。其次是用于MNIST数据集的网络结构。
在上世界50年代,深度神经网络的概念就已出现,从理论上来讲可以解决众多问题,但是一直以来却没有人知道该如何训练它,渐渐的也就被放弃。直至1986年,Hinton想到了通过反向传播来训练深度网络,标志了深度学习发展的一大转机。然而,受限于当时的计算机运算能力,直到2012年,Hinton的发明才得以一显神通。这一突破也为近年来人工智能的发展奠定了基础。
CNN通过多层卷积层不断增加感受野实现了从边缘检测到简单的形状特征、再到最终复杂模式的识别,由于卷积核的工作方式,卷积神经网络拥有平移不变性。然而,特征之间的空间关系是卷积神经网络无法提取的。这是什么意思?看下面的例子就能明白。
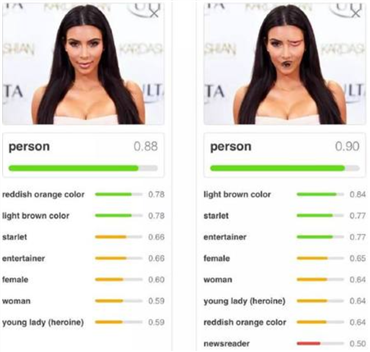
上图中,将人的左眼和嘴巴的位置进行调换,这已经不是一个正确的人脸了,特征的空间位置明显是错误的,但是CNN仍将其识别为人。CNN还有另一个缺陷,就是在查看不同方向的图像时容易产生混淆,如下图所示:
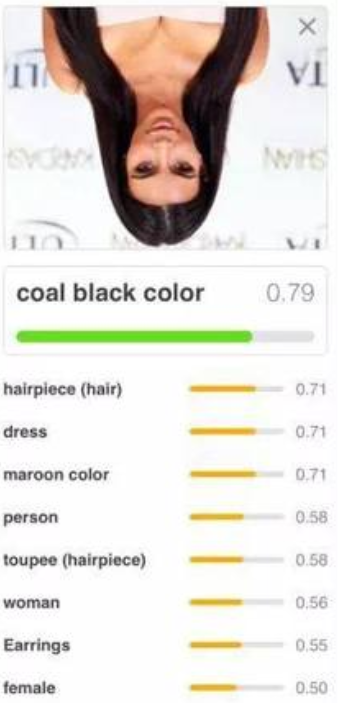
通过将图片进行旋转180度,CNN已经无法正确将其识别为人。这可以通过数据增加来解决,即在训练时对图片进行旋转,但是增加了训练的时间。
胶囊网络解决了这样的问题,因为每个胶囊能够识别一种实体,或者说一种模式,以激活向量的形式来表示。激活向量的每个维度可能对应该模式的一些变化,如旋转的角度。
两层胶囊网络之间连接使用全连接方式。前一层所有个胶囊的输出与后一层每个胶囊相连。假设,前一层有3个胶囊,现在,我们先来考虑后一层的某一个胶囊\(j\)。每个胶囊的输出是一个向量,因此,前一层胶囊的输出就是\(\mathbf{u}_1,\mathbf{u}_2, ..., \mathbf{u}_n\)。首先,需要进行一次变换,每个前一层的输出需要分别与某个矩阵相乘,编程另一个向量。即:
接着,对每个\(\mathbf{\hat{u}}_{j|i}\)进行加权求和,权重分别对应为\(c_{1j}, c_{2j}, ..., c_{nj}\):
最后得到这个胶囊的输出:
公式(3)称作squash,该操作将激活向量的模长限制在\(\left[0, 1\right]\)。看左边的分式,当\(\mathbf{s}_j\)的模长很长时,分式的值趋近于1;当\(\mathbf{s}_j\)的模长很短时,分式趋近于0。这就是为什么激活向量的模长是某种模式被该胶囊识别的概率。
\(\mathbf{W}_{ij}\)是模型的参数,需要通过反向传播进行学习得到。而权重参数\(c_{ij}\)则不是通过反向传播得到的,而是通过动态路由算法得到的。该算法是一种迭代算法。首先,对每个\(\mathbf{\hat{u}}_{j|i}\),我们为其初始化一个参数\(b_{ij}\),初始化的值为0,然后开始迭代算法。假设迭代次数为T。每次迭代的过程如下:
对所有的\(b_{ij}\),先进行\(softmax\)操作,得到\(c_{ij}\):
使用得到的\(c_{ij}\)进行加权求和得到向量\(s_j\),注意这不是胶囊的输出:
对\(s_{j}\)进行squash操作
更新\(b_{ij}\)的值:
经过T次迭代后,得到的\(\mathbf{v}_j\)就是该胶囊的激活向量,也就是输出向量。这个动态路由算法中,与\(\mathbf{v}_j\)点乘的值更大的\(mathjbf{\hat{u}}_{j|i}\)被赋予更高的权重。
整个算法流程如下图:

这篇文章中实验部分用到的网络叫做CapsNet,有两个卷积层和一个全连接层组成,当然,这个全连接层是胶囊层,不是普通人工神经网络层。其网络结构如下:
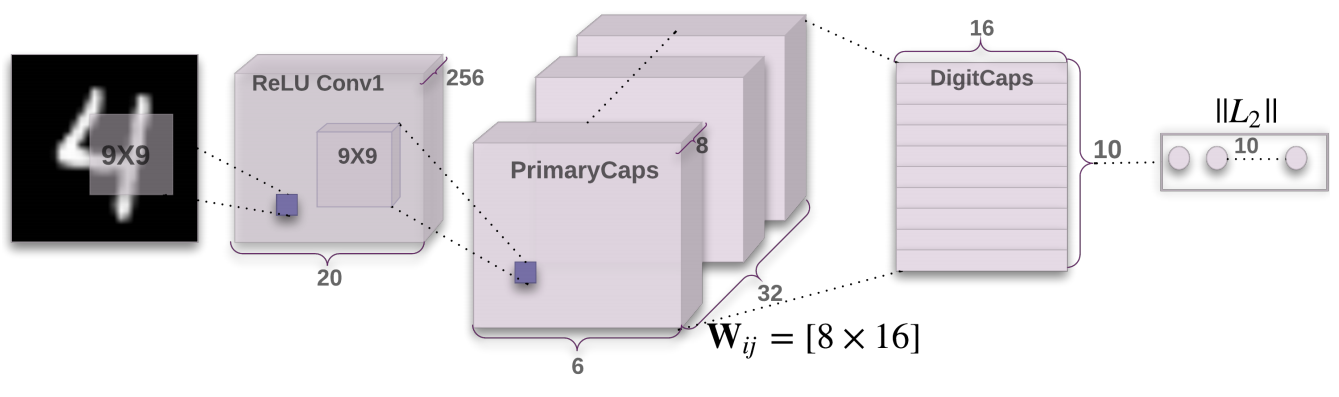
第一层卷积层是普通的卷积层,卷积核大小为9x9,stride为1,channel为256。
第二层叫做Primary Capsule,文中对该层的描述我个人没有看懂,但是看过代码,以及网上其他人的讲解,其本身就是一个卷积层,卷积核大小为9,stride为2,channel为256,只不过在最后先对其进行了一个reshape使得其维度与第三层维度相匹配,即本来得出的维度是6x6x256,将其respahe成了1152x8。
第三层是一个Capsule层,有10个Capsule,对应MNIST的10个类别。变换矩阵\(\mathbf{W}_{ij}\)的维度为8x16,将一层的每个8维向量转换成16维向量。最后的预测类别是该层的10个激活向量中的模长最大的Capsule对应的类别。
除了分类网络以外,还有另一个拓展的网络,即重构网络,通过将Capsule层的输出送到全连接层中进行重构。网络结构如下所示:
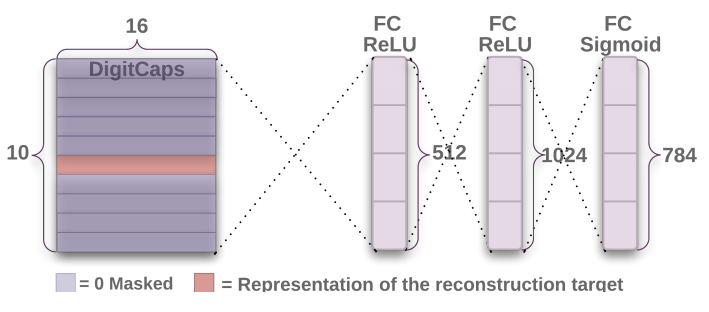
这里需要进行一步Mask操作,即对于Capsule层的预测输出,只保留预测的类别对应的Capsule的激活向量的值,即模长最大的那个Capsule的激活向量,其他的Capsule的激活向量全部被Mask成0。然后进行Reshape操作形成一个含160个元素的一维向量。第一层全连接层的输出维度为512,第二层全连接层的输出维度为1024,最后一层的全连接层的输出维度为784,当然最后接了一个Sigmoid激活函数。前两层接的是ReLU激活函数。
对于分类网络而言,Capsule层的每个Capsule的输出,都会计算一个损失值:
其中\(T_k\)的值在第\(k\)个胶囊预测结果正确时为1,错误时为0。该损失与交叉熵损失很像。\(m^+\)取0.9,\(m^-\)取0.1,\(\lambda\)取0.5。某个输入的损失就是简单地把这次对该输入的预测的Capsule层的十个胶囊的该损失求和。
而对于重构损失,简单的计算重构的每个像素值与原始输入图片的像素值的平方损失。
整个训练过程中将分类损失与重构损失加起来就是最终的损失函数,用于反向传播。
这个实验中,使用原始的MNIST数据集,数据增强操作仅仅是用了2个像素位置的随机Crop,并使用0填充。分类的实验结果如下:
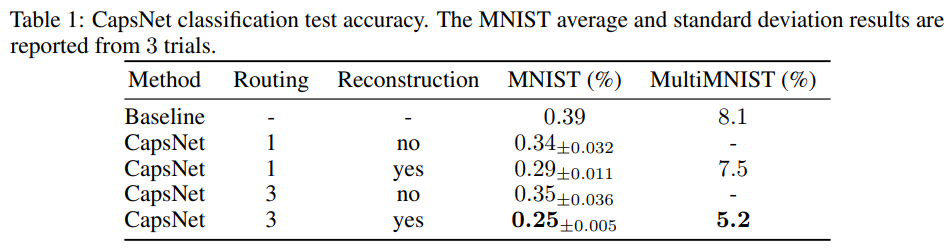
Baseline是一个传统的卷积神经网络接全连接层的架构。可以看到,3次迭代Routing比1次迭代的动态路由效果要好,两外,加上重构任务比不加上重构任务的效果要好。
下面看看重构的结果:
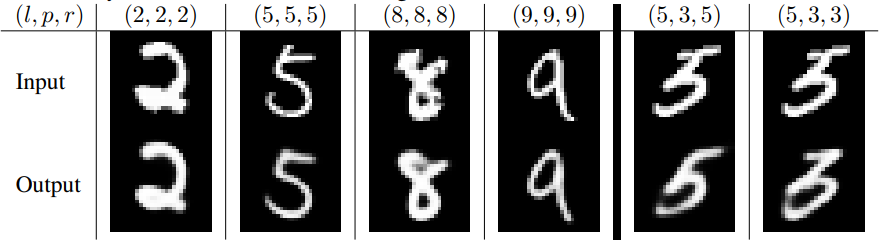
\(l\)表示原始的标签,\(p\)表示预测的结果,\(r\)表示重构的结果。最右边的两列是用预测错误的结果进行重构的,它可以重构出5,也可以重构出3。
此外,实验还对比了传统的CNN和CapsNet对仿射变换的鲁棒性,CapsNet的鲁棒性要好于CNN。
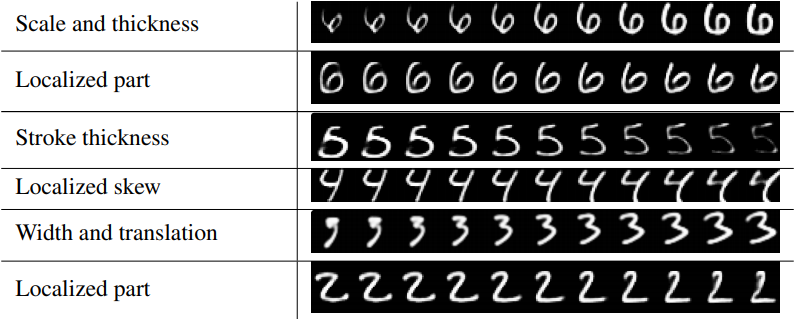
还有一个有趣的实验,通过修改Capsule层输出向量的某个维度的值,可以发现重构的图片笔划的粗细等呈现出不一样的特性,这表明,Capsule的激活向量捕获了某种模式,其每个维度可能都代表了该模式的某些特征,如笔划的粗细。
MultiMNIST是用MNIST生成的一个重叠手写体数字数据集,MNIST中的每张图片生成了1000张重叠的手写体数字图片。我们来看看重构的结果:

主要看到带星号的两列。看第一行,原始的标签是(5, 0),现在我们让它重构出(5, 7),它无法重构出7,因为它学习到了图片中原来没有7。同样,对于其他的例子也一样。网络能够从原本的Label或者预测的Label重构出对应的数字,却不能重构出除二者之外的数字。
论文阅读之Dynamic Routing between Capsules
原文:https://www.cnblogs.com/lewki/p/14120989.html