剑指 Offer 42. 连续子数组的最大和

题目链接

1. 状态定义： 设动态规划列表 \(dp\) ，\(dp[i]\) 代表以元素 \(4nums[i]\) 为结尾的连续子数组最大和。

2. 为何定义最大和 \(dp[i]\) 中必须包含元素 \(nums[i]\) ：保证 \(dp[i]\) 递推到 \(dp[i+1]\) 的正确性；如果不包含 \(nums[i]\) ，递推时则不满足题目的 连续子数组 要求。

3. 转移方程： 若 \(dp[i-1] \leq 0\) ，说明 \(dp[i - 1]\) 对 \(dp[i]\) 产生负贡献，即 \(dp[i-1] + nums[i]\) 还不如 \(nums[i]\) 本身大。

   • 当 \(dp[i - 1] > 0\) 时：执行 \(dp[i] = dp[i-1] + nums[i]\) ；
   • 当 \(dp[i - 1] \leq 0\) 时：执行 \(dp[i] = nums[i]\) ；
     

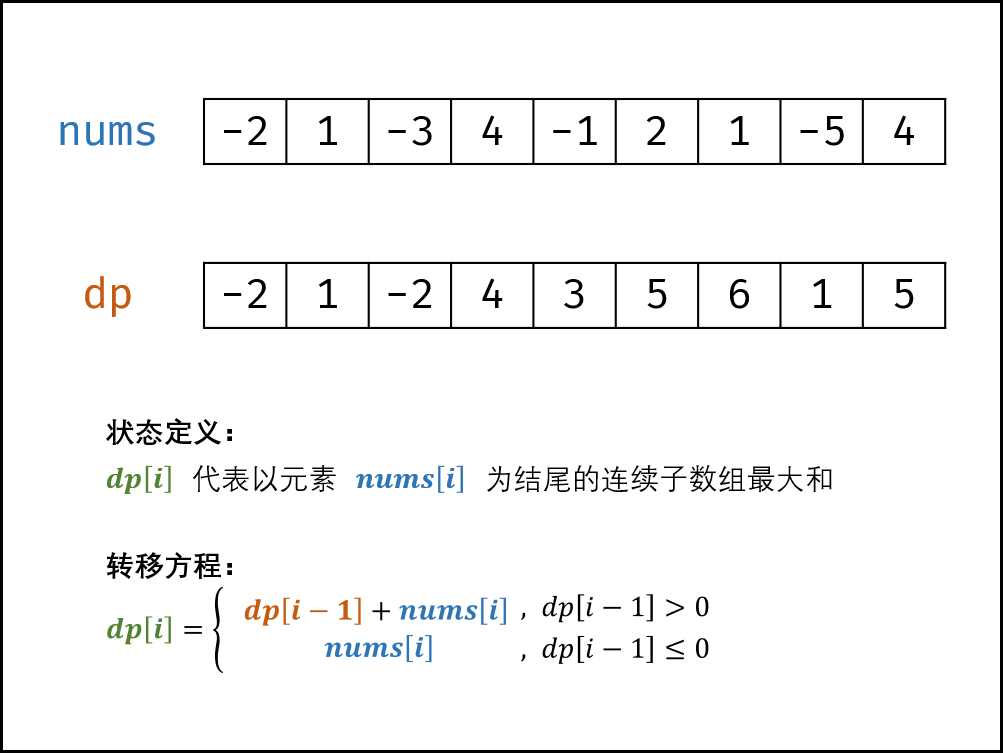
4. 初始状态： \(dp[0] = nums[0]\)，即以 \(nums[0]\) 结尾的连续子数组最大和为 \(nums[0]\) 。

5. 返回值： 返回 dp 列表中的最大值，代表全局最大值。

6. 空间复杂度降低：

   • 由于 \(dp[i]\) 只与 \(dp[i-1]\) 和 \(nums[i]\) 有关系，因此可以将原数组 \(nums\) 用作 \(dp\) 列表，即直接在 nums 上修改即可。
     *由于省去 dp 列表使用的额外空间，因此空间复杂度从 \(O(N)\) 降至 \(O(1)\) 。

7. 复杂度分析：

   • 时间复杂度 \(O(N)\) ： 线性遍历数组 nums即可获得结果，使用 \(O(N)\) 时间。
   • 空间复杂度 \(O(1)\) ： 使用常数大小的额外空间。

package com.walegarrett.offer;

/**
 * @Author WaleGarrett
 * @Date 2020/12/12 8:34
 */
public class Offer_42 {
    public int maxSubArray(int[] nums) {
        int len = nums.length;
        int sum = 0;
        int maxs = -0x3f3f3f3f;
        for(int i=0; i<len; i++){
            sum += nums[i];
            maxs = Math.max(maxs, sum);
            if(sum < 0){
                sum = 0;
            }
        }
        return maxs;
    }
}

剑指 Offer 42. 连续子数组的最大和 + 动态规划

原文：https://www.cnblogs.com/GarrettWale/p/14123706.html