在无限的整数序列 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...中找到第 n 个数字。
输入:
11
输出:
0
说明:
第11个数字在序列 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ... 里是0,它是10的一部分。
暴力破解
class Solution:
@classmethod
def findNthDigit(self, n: int) -> int:
li = []
for i in range(1,n+1):
li.append(str(i))
str_li = ‘‘.join(li)
return str_li[n-1]
class Solution:
def findNthDigit(self, n: int) -> int:
# 首先判断target是几位数,用digits表示
base = 9
digits = 1
while n - base * digits > 0:
n -= base * digits
base *= 10
digits += 1
# 计算target的值
idx = n % digits # 注意由于上面的计算,n现在表示digits位数的第n个数字
if idx == 0:
idx = digits
number = 1
for i in range(1,digits):
number *= 10
if idx == digits:
number += n // digits - 1
else:
number += n // digits
# 找到target中对应的数字
for i in range(idx,digits):
number //= 10
return number % 10
比如输入的 n 是 365:
经过第一步计算我们可以得到第 365 个数字表示的数是三位数,n=365-9-90\times2=176n=365?9?90×2=176,digtis = 3。这时 n=176n=176 表示目标数字是三位数中的第 176176 个数字。
我们设目标数字所在的数为 number,计算得到 number=100+176/3=158number=100+176/3=158,idx 是目标数字在 number 中的索引,如果 idx = 0,表示目标数字是 number - 1 中的最后一个数字。(感谢@1m188 更正为 number-1)
根据步骤2,我们可以计算得到 idx = n % digits = 176 % 3 = 2,说明目标数字应该是 number = 158 中的第二个数字,即输出为 5。
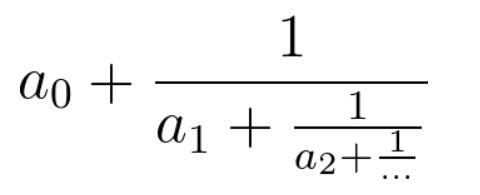
输入的cont代表连分数的系数(cont[0]代表上图的a0,以此类推)。返回一个长度为2的数组[n, m],使得连分数的值等于n / m,且n, m最大公约数为1。
输入:cont = [3, 2, 0, 2]
输出:[13, 4]
解释:原连分数等价于3 + (1 / (2 + (1 / (0 + 1 / 2))))。注意[26, 8], [-13, -4]都不是正确答案。
输入:cont = [0, 0, 3]
输出:[3, 1]
解释:如果答案是整数,令分母为1即可。
class Solution:
def fraction(self, cont: List[int]) -> List[int]:
numerator = 1 #分子
denominator = cont[-1] #分母
for i in range(len(cont)-1,0,-1):
numerator,denominator = denominator,numerator
denominator = cont[i-1]*numerator+denominator
return [denominator,numerator]
通分即可,停止条件为遍历完数组中所有数。
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
此题中,我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
输入:nums = [2,0,1]
输出:[0,1,2]
class Solution:
@classmethod
def sortColors(self, nums: list) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
len_li = len(nums)
if len_li == 1:
return nums
# [0,p1) 0
# [p2,n) 1
# [p1,p2) 2
p_0 = 0
i = 0
p_1 = 0
p_2 = len_li - 1
while i <= p_2:
if nums[i] == 0:
nums[i],nums[p_1] = nums[p_1],nums[i]
i += 1
p_1 += 1
elif nums[i] == 1:
i += 1
else:
nums[i],nums[p_2] = nums[p_2],nums[i]
# i += 1
p_2 -= 1
荷兰旗方法,[0,p1) 最小,[p1,p2)中间,[p2,n]最大,i为什么要小于等于p2作为终止条件,因为p2也要做一次判断,这样一次遍历可以对整个数组进行排序。
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4
手写快速排序。
快速排序:每次快速排序都会有个pivot索引,跟k进行比较,另外一部分不用排序。
堆排序:大根堆。掌握大根堆的建立,删除,了解大根堆的建立,删除,调整的逻辑
class Solution {
public int findKthLargest(int[] nums, int k) {
int heapSize = nums.length;
buildMaxHeap(nums, heapSize);
for (int i = nums.length - 1; i >= nums.length - k + 1; --i) {
swap(nums, 0, i);
--heapSize;
maxHeapify(nums, 0, heapSize);
}
return nums[0];
}
public void buildMaxHeap(int[] a, int heapSize) {
for (int i = heapSize / 2; i >= 0; --i) {
maxHeapify(a, i, heapSize);
}
}
public void maxHeapify(int[] a, int i, int heapSize) {
int l = i * 2 + 1, r = i * 2 + 2, largest = i;
if (l < heapSize && a[l] > a[largest]) {
largest = l;
}
if (r < heapSize && a[r] > a[largest]) {
largest = r;
}
if (largest != i) {
swap(a, i, largest);
maxHeapify(a, largest, heapSize);
}
}
public void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
输入:
Tree 1 Tree 2
1 2
/ \ / \
3 2 1 3
/ \ \
5 4 7
输出:
合并后的树:
3
/ 4 5
/ \ \
5 4 7
DFS
class Solution:
def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
if not t1:
return t2
if not t2:
return t1
merged = TreeNode(t1.val + t2.val)
merged.left = self.mergeTrees(t1.left, t2.left)
merged.right = self.mergeTrees(t1.right, t2.right)
return merged
BFS
class Solution:
def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:
if not t1:
return t2
if not t2:
return t1
merged = TreeNode(t1.val + t2.val)
queue = collections.deque([merged])
queue1 = collections.deque([t1])
queue2 = collections.deque([t2])
while queue1 and queue2:
node = queue.popleft()
node1 = queue1.popleft()
node2 = queue2.popleft()
left1, right1 = node1.left, node1.right
left2, right2 = node2.left, node2.right
if left1 or left2:
if left1 and left2:
left = TreeNode(left1.val + left2.val)
node.left = left
queue.append(left)
queue1.append(left1)
queue2.append(left2)
elif left1:
node.left = left1
elif left2:
node.left = left2
if right1 or right2:
if right1 and right2:
right = TreeNode(right1.val + right2.val)
node.right = right
queue.append(right)
queue1.append(right1)
queue2.append(right2)
elif right1:
node.right = right1
elif right2:
node.right = right2
return merged
困在了null和非null的合并,其实直接赋值就可以了,停止遍历,不需要考虑null子节点的情况。
原文:https://www.cnblogs.com/jimmyhe/p/14124226.html