图像处理论文详解 | Deformable Convolutional Networks | CVPR | 2017

文章转自同一作者的微信公众号：【机器学习炼丹术】

• 论文名称：“Deformable Convolutional Networks”
• 论文链接：https://arxiv.org/abs/1703.06211

0 前言

首先理解：

• deformable Convolution可变卷积针对的对象是卷积本身，因此膨胀卷积，3D卷积都可以用可变卷积的形式
• 本篇文章讲解理论和论文，我还没有用上这个可变卷积测试效果，因为PyTorch好像还没有封装这个卷积方式，有点麻烦。所以我计划下一篇文章结合github上已经有的pytorch复现的可变卷积来做一个简单的测试。
• 本来我是在学轮廓检测算法的，看到了一个SOTA的算法叫做deep snake，然后看了半天代码，发现里面嵌套了DCN，DLA等多个算法，所以就从头开始学了。

1 论文概述

论文中作者最大的贡献为：

1. 提出了可变卷积，可变卷积网络为Deformable ConvNet（DCN）。
2. 用同样的原理提出了可变池化层，叫做deformable ROI pooling。
3. 这两个模块可以非常简单的用在其他网络结构中，并且不会增加很多的参数，但是效果还是不错的。（论文把这个方法用在了主流模型中）。

这个核心贡献在于，为什么卷积过程中卷积核一定要是正方形的？我的检测目标各种形状都有，为什么卷积核一定要是正方形的呢？

因此，这里的卷积核不再是正方形了，而是可以通过梯度下降更新的参数了：

a图就是最基本的卷积核，b就是可变卷积的卷积核，c和d是可变卷积的特殊情况。听起来不难吧，原理确实非常的简单。

2 实现原理

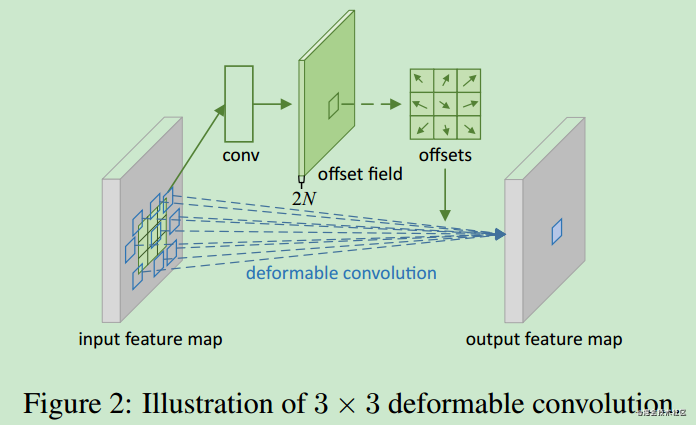
上图是表示可变卷积过程的。大概看一眼这个图，不难发现这种结构似乎和SEnet有点类似。在下一篇的代码实战中再考虑如何实现这个过程把。

泛泛地说的话，就是这个特征图，再额外的经过一个卷积层，生成一个offset的结果，然后把这个offset和这个特征图融合。

3 实验结果

论文中提到，在特征提取网络的后面3层使用可变卷积的效果比较好。

上图是在实际任务中，deformable convnets学习到的采样点，我认为这是一种非常有意思的可解释性的体现。

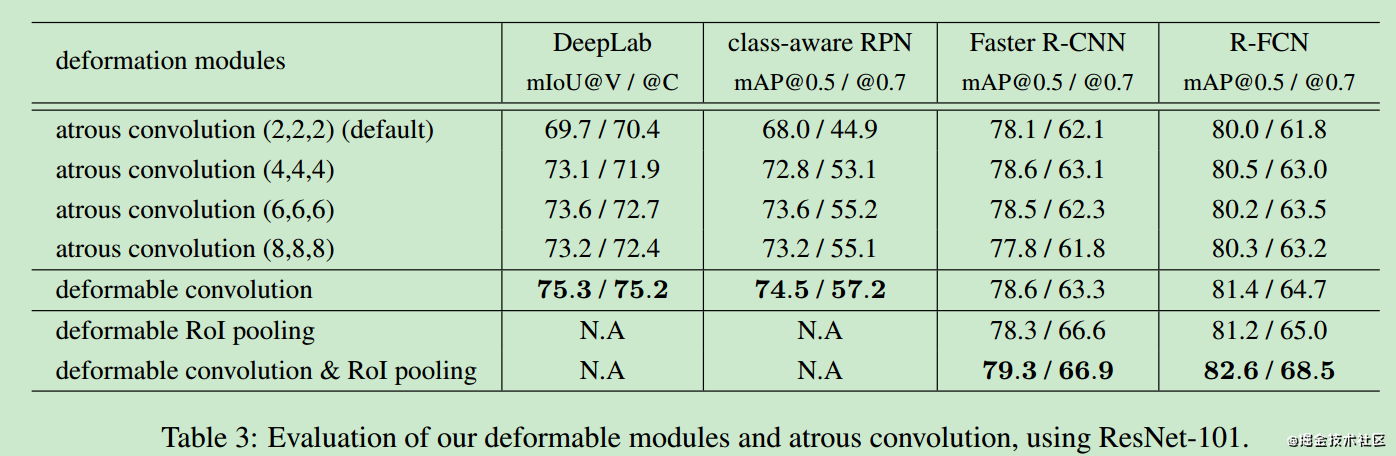
上表中最后三行体现了这个可变卷积的效果，确实是不错，确实有一定提升，那么这种可变卷积对与参数量的影响大吗？

可以看到，这个参数的影戏那个微乎其微，运行时间也基本差不多。我决定等我复现了这个可变卷积之后，我在以后的模型中都要用这个试试能不能有提升。（奇怪的奇技淫巧又增加了）。

大概就这么多，从理论上看，这个deformable convolution不难，关键是如何实现，希望我在复现的过程上不会太坎坷。

参考文章：

1. https://arxiv.org/abs/1703.06211
2. https://littletomatodonkey.github.io/2018/12/02/2018-12-02-Deformable ConvNets/
3. https://zhuanlan.zhihu.com/p/52476083

图像处理论文详解 | Deformable Convolutional Networks | CVPR | 2017

原文：https://www.cnblogs.com/PythonLearner/p/14157773.html