这篇博客分为两部分。首先我会先讲极大极小算法，然后在此基础上进行改进给出进阶版的Alpha-Beta剪枝算法以及代码实现。文中配备b站讲解的视频，感兴趣的可以看一下视频讲解，然后复习的时候拿着文章当作参考。

Minimax算法（极大极小算法）

概念

• 是一种找出最小失败的可能的算法。意思就是两个人下棋，A和B下棋，A想要自己的利益最大化（失败的可能性最小），B想要A的利益最小化（B想要A输）。这个算法以及接下来的Alpha-Beta剪枝都是一种对抗性搜索算法（两个人互相对抗着下棋，俩人都想赢），是一种人工智能搜索的算法。掌握此算法后可以用来写井字棋、五子棋等人工智能人机对抗下棋程序。

具体步骤

给你一颗二叉树。告诉你小紫和小黑玩游戏。紫色和黑色圆圈代表他们两个。我们是站在小紫的角度来描述的。小紫想要他自己的得分最大 所以小紫玩的时候，二叉树的那一层叫MAX层。小黑想要小紫的得分最小化，小黑的叫做MIN层。我们总是让小紫第一个开始，假设下面这个二叉树，我们只知道叶子节点的值（别管为啥，先学好算法原理，后续如何应用这个算法我还打算继续写博客和录视频讲解。）：

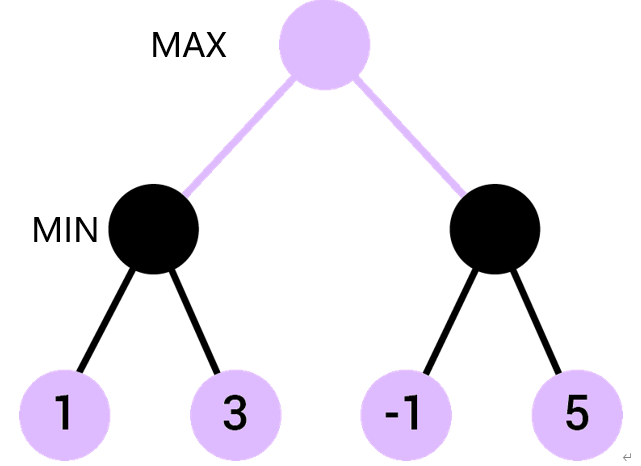
在这里给出定义，MAX层的节点的值是什么？？是它的子节点里面的最大值，MIN层的值是它的子节点里面的最小值。直接上图。
MIN层是选择其孩子节点中最小值。

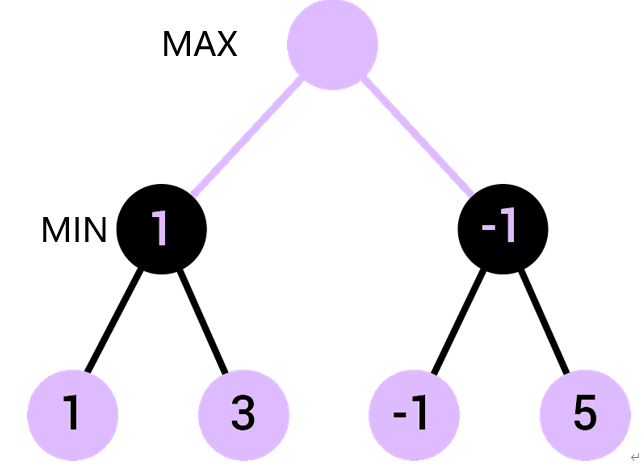
MAX层选择其孩子节点中的最大值。

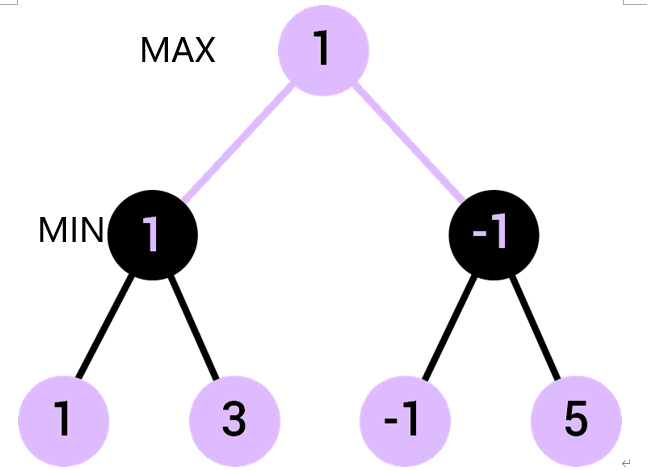
算法概念就是这个样子。
算法的输入是构造的这一棵满二叉树，输出是最上层MAX节点的值。

代码实现

class Node{     //结点类
public:
	const int value;
	Node *left;
	Node *right;
	Node(int v,Node* l,Node* r):value(v),left(l),right(r)  {};
  };

为了遍历这棵树，首先我们得创建出来这棵树对吧？但是你的代码里没有创建二叉树这一部分啊。别急，一会给出完整代码，现在先专注于这个算法是如何实现的。
我们的思路是，对于每一个节点，无论是max层的还是min层的，从下往上我们要知道这个节点的值。利用递归和设置一个min1和max1变量记录。同时return的min1和max1也是上一层结点值。

int minimax(Node* position, bool who){
if(position->left == NULL){
return position->value;	
  }  //叶子结点  结束递归。 
  
  if(who){// max
  int max1 = INT_MIN;
  int value = minimax(position->left,false);//左孩子 
  max1 = std::max(value,max1);
  
  value = minimax(position->right,false);//右孩子 
  max1 = std::max(value,max1);	  	
  
  return max1;
  
  }
  
  else {//min
  int min1 = INT_MAX;
  int value = minimax(position->left,true);//左孩子 
  min1 = std::min(value,min1);
  
  value = minimax(position->right,true);//右孩子 
  min1 = std::min(value,min1);	
  
  return min1;
  }

}

Alpha-Beta剪枝算法

概念

在minimax算法的基础上，为了缩减时间而进行的剪枝操作。
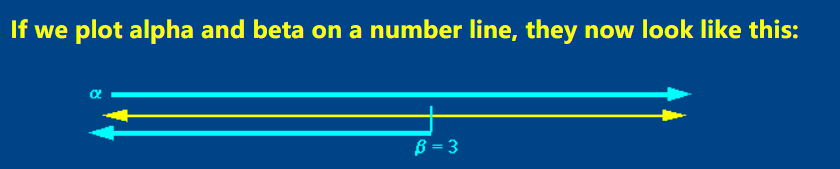
在原来的基础上，有的层是MIN层，有的是MAX层。现在在原来max1值和min1值的基础上设置alpha和beta。如图，这是alpha和beta的初始值为负无穷和正无穷，通过递归的调用向下传递。在MAX层更新alpha值，在MIN层更新beta值。alpha和beta只向下传递（通过一层一层的递归调用，一开始那些最左边的、一层一层往下传的alpha和beta都是负无穷和正无穷。）


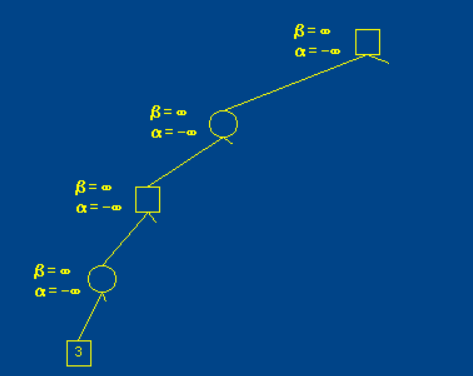
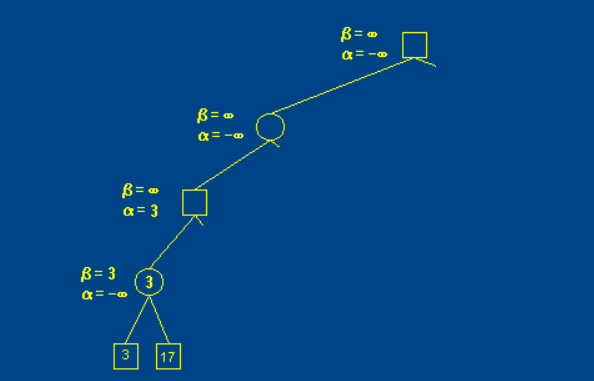
下图，往父节点返回值。更新alpha。

下图，我们快进了一些内容，直接跳到剪枝的部分。

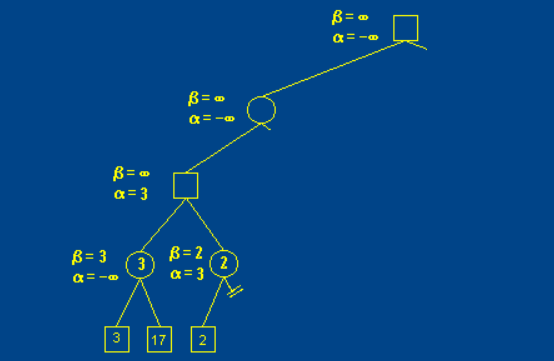
当alpha<=beta时剪枝

代码实现

int alpha_beta_pruning(Node* position, int alpha, int beta, bool who){
if(position->left == NULL){
	return position->value;	
  }
  
  if(who){// max
  int max1 = INT_MIN;
  int value = alpha_beta_pruning(position->left,alpha,beta,false);
  max1 = std::max(value,max1);
  alpha = std::max(alpha,max1);
  if(beta <= alpha){
  	delete_subtree(position->right);  //剪枝只发生在右边
  	position->right = NULL;
  	return max1;
  } 
  
  value = alpha_beta_pruning(position->right,alpha,beta,false);
  max1 = std::max(value,max1);
  return max1;
  
  }
  else {//min
  int min1 = INT_MAX;
  int value = alpha_beta_pruning(position->left,alpha,beta,true);
  min1 = std::min(value,min1);
  beta = std::min(beta,min1);
  if(beta <= alpha){
  	delete_subtree(position->right);  //剪枝只发生在右边
  	position->right = NULL;
  	return min1;
  }
  
  value = alpha_beta_pruning(position->right,alpha,beta,true);
  min1 = std::min(value,min1);
  return min1;
  }

}

剪枝时delete函数

    void delete_subtree(Node* position) {
    if (position -> left != NULL){
      delete_subtree(position -> left);
      position -> left = NULL;
    }
    if (position -> right != NULL){
      delete_subtree(position -> right);
      position -> right = NULL;
    }
    delete position; 
  }

Minimax极大极小算法、Alpha-Beta Pruning剪枝算法

原文：https://www.cnblogs.com/juzijuziju/p/14178053.html