炮弹发射视为斜抛运动,已知初始速度为200m/s,问要击中水平距离360m、垂直距离160m的目标,当忽略空气阻力时,发射角应多大?此时炮弹的运行轨迹如何?试进行动态模拟。进一步思考:如果要考虑水平方向的阻力,且设阻力与(水平方向)速度成正比,系数为0.1(1/s),结果又如何?此时炮弹的运行轨迹如何?试进行动态模拟。
当忽略空气阻力时
在水平方向,炮弹的速度不变,t时刻的运动方程为
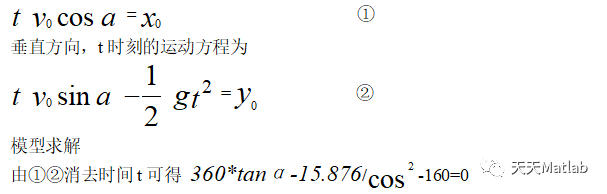
sita=-6:0.1:2*pi;y=360*tan(sita)-15.876./cos((sita).^2)-160;plot(sita,y,‘b‘)grid onhold on y1=0;ezplot(y1)axis([-6,6,-16000,35000])?
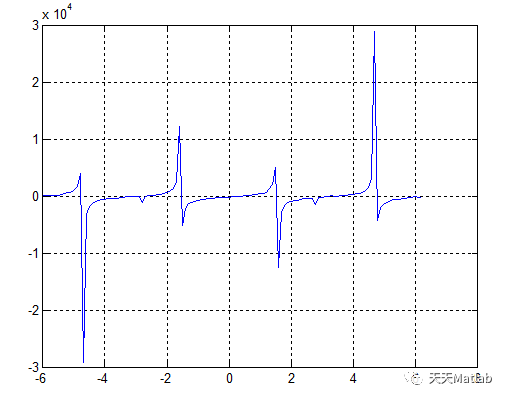
由图可知在0到π之间,方程有两个解,分别是0~1之间,1~2之间,3~4之间,在0~1由图形放大法分别由MATLAB绘制图形。程序如下:
a=0:0.1:2*pi; y=360*tan(a)-15.876./cos((a).^2)-160;subplot(2,2,1),plot(a,y),axis([0.4,0.5,-200,200]),grid on subplot(2,2,2),plot(a,y),axis([0.42,0.48,-100,100]),grid on subplot(2,2,3),plot(a,y),axis([0.45,0.46,-10,10]),grid onsubplot(2,2,4),plot(a,y),axis([0.453,0.456,-4,4]),grid on
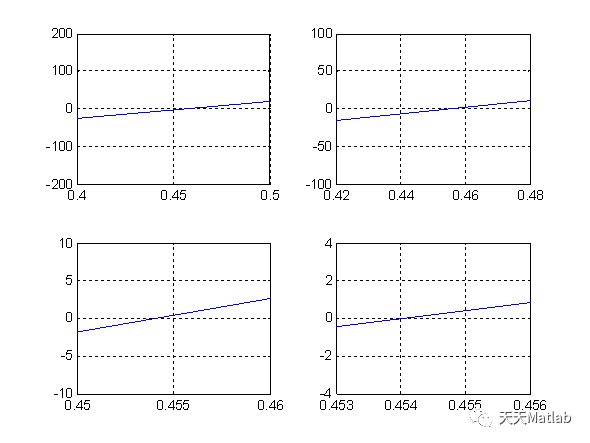
所以在0~1之间的近似解为0.454;同理可绘制1~2之间的图像。程序如下:
a=0:0.1:2*pi; y=360*tan(a)-15.876./cos((a).^2)-160; subplot(2,2,1),plot(a,y),axis([1,2,-200,200]),grid on subplot(2,2,2),plot(a,y),axis([1.4,1.6,-10,10]),grid onsubplot(2,2,3),plot(a,y),axis([1.52,1.54,-1,1]),grid on subplot(2,2,4),plot(a,y),axis([1.527,1.529,-0.0001,0.0001]),grid on
由图可知其解近似为1.528。所以当不考虑空气阻力时,发射角大约为0.454或1.528。如果要考虑水平方向的阻力,且设阻力与(水平方向)速度成正比,系数为 0.1(1/s)。垂直方向仍满足
sita=0.1:0.01:0.5;y=1.6+20*tan(sita).*log(1-36*cos(sita)./200)+4.9*(log((1-36*cos(sita)./200))).^2./(cos(sita)).^2;plot(sita,y),grid on
在1~2之间的值满足a在0~pi,用图形放大法观察。
sita=0.45:0.01:0.5;y=1.6+20*tan(sita).*log(1-36*cos(sita)./200)+4.9*(log((1-36*cos(sita)./200))).^2./(cos(sita)).^2;plot(sita,y),grid on
所以考虑空气阻力时,发射的角度近似为a=0.475。当然这个不是精确解,要得到精确解,可以尝试solve或者fsolve函数。
注:完整代码或者代写添加QQ1575304183
原文:https://www.cnblogs.com/homeofmatlab/p/14206648.html