线性表是最基本、最简单、也是最常用的一种数据结构。一个线性表是n个具有相同特性的数据元素的有限序列。

前驱元素:
若A元素在B元素的前面,则称A为B的前驱元素
后继元素:
若B元素在A元素的后面,则称B为A的后继元素
线性表的特征:数据元素之间具有一种“一对一”的逻辑关系。
1 . 第一个数据元素没有前驱,这个数据元素被称为头结点;
最后一个数据元素没有后继,这个数据元素被称为尾结点;
除了第一个和最后一个数据元素外,其他数据元素有且仅有一个前驱和一个后继。
如果把线性表用数学语言来定义,则可以表示为(a1,...ai-1,ai,ai+1,...an),ai-1领先于ai,ai领先于ai+1,称ai-1是ai的
前驱元素,ai+1是ai的后继元素

线性表的分类:
线性表中数据存储的方式可以是顺序存储,也可以是链式存储,按照数据的存储方式不同,可以把线性表分为顺序
表和链表。
顺序表是在计算机内存中以数组的形式保存的线性表,线性表的顺序存储是指用一组地址连续的存储单元,依次存储线性表中的各个元素、使得线性表中再逻辑结构上响铃的数据元素存储在相邻的物理存储单元中,即通过数据元素物理存储的相邻关系来反映数据元素之间逻辑上的相邻关系。

顺序表API设计:

顺序表的代码实现:
// 顺序表代码
public class SequenceList<T> {
//存储元素的数组
private T[] eles;
//记录当前顺序表中的元素个数
private int N;
//构造方法
public SequenceList(int capacity){
eles = (T[])new Object[capacity];
N=0;
}
//将一个线性表置为空表
public void clear(){
N=0;
}
//判断当前线性表是否为空表
public boolean isEmpty(){
return N==0;
}
//获取线性表的长度
public int length(){
return N;
}
//获取指定位置的元素
public T get(int i){
if (i<0 || i>=N){
throw new RuntimeException("当前元素不存在!");
}
return eles[i];
}
//向线型表中添加元素t
public void insert(T t){
if (N==eles.length){
throw new RuntimeException("当前表已满");
}
eles[N++] = t;
}
//在i元素处插入元素t
public void insert(int i,T t){
if (i==eles.length){
throw new RuntimeException("当前表已满");
}
if (i<0 || i>N){
throw new RuntimeException("插入的位置不合法");
}
//把i位置空出来,i位置及其后面的元素依次向后移动一位
for (int index=N;index>i;index--){
eles[index]=eles[index-1];
}
//把t放到i位置处
eles[i]=t;
//元素数量+1
N++;
}
//删除指定位置i处的元素,并返回该元素
public T remove(int i){
if (i<0 || i>N-1){
throw new RuntimeException("当前要删除的元素不存在");
}
//记录i位置处的元素
T result = eles[i];
//把i位置后面的元素都向前移动一位
for (int index=i;index<N-1;index++){
eles[index]=eles[index+1];
}
//当前元素数量-1
N--;
return result;
}
//查找t元素第一次出现的位置
public int indexOf(T t){
if(t==null){
throw new RuntimeException("查找的元素不合法");
}
for (int i = 0; i < N; i++) {
if (eles[i].equals(t)){
return i;
}
}
return -1;
}
}
//测试代码
public class SequenceListTest {
public static void main(String[] args) {
//创建顺序表对象
SequenceList<String> sl = new SequenceList<>(10);
//测试插入
sl.insert("姚明");
sl.insert("科比");
sl.insert("麦迪");
sl.insert(1,"詹姆斯");
//测试获取
String getResult = sl.get(1);
System.out.println("获取索引1处的结果为:"+getResult);
//测试删除
String removeResult = sl.remove(0);
System.out.println("删除的元素是:"+removeResult);
//测试清空
sl.clear();
System.out.println("清空后的线性表中的元素个数为:"+sl.length());
}
}
一般作为容器存储数据,都需要向外部提供遍历的方式,因此我们需要给顺序表提供遍历方式。
在 java中,遍历集合的方式一般都是用的是foreach循环,如果想让我们的SequenceList也能支持foreach循环,则需要做如下操作:
1.让SequenceList实现Iterable接口,重写iterator方法;
2.在SequenceList内部提供一个内部类SIterator,实现Iterator接口,重写hasNext方法和next方法;
代码:
// 顺序表代码
import java.util.Iterator;
public class SequenceList<T> implements Iterable<T>{
//存储元素的数组
private T[] eles;
//记录当前顺序表中的元素个数
private int N;
//构造方法
public SequenceList(int capacity){
eles = (T[])new Object[capacity];
N=0;
}
//将一个线性表置为空表
public void clear(){
N=0;
}
//判断当前线性表是否为空表
public boolean isEmpty(){
return N==0;
}
//获取线性表的长度
public int length(){
return N;
}
//获取指定位置的元素
public T get(int i){
if (i<0 || i>=N){
throw new RuntimeException("当前元素不存在!");
}
return eles[i];
}
//向线型表中添加元素t
public void insert(T t){
if (N==eles.length){
throw new RuntimeException("当前表已满");
}
eles[N++] = t;
}
//在i元素处插入元素t
public void insert(int i,T t){
if (i==eles.length){
throw new RuntimeException("当前表已满");
}
if (i<0 || i>N){
throw new RuntimeException("插入的位置不合法");
}
//把i位置空出来,i位置及其后面的元素依次向后移动一位
for (int index=N;index>i;index--){
eles[index]=eles[index-1];
}
//把t放到i位置处
eles[i]=t;
//元素数量+1
N++;
}
//删除指定位置i处的元素,并返回该元素
public T remove(int i){
if (i<0 || i>N-1){
throw new RuntimeException("当前要删除的元素不存在");
}
//记录i位置处的元素
T result = eles[i];
//把i位置后面的元素都向前移动一位
for (int index=i;index<N-1;index++){
eles[index]=eles[index+1];
}
//当前元素数量-1
N--;
return result;
}
//查找t元素第一次出现的位置
public int indexOf(T t){
if(t==null){
throw new RuntimeException("查找的元素不合法");
}
for (int i = 0; i < N; i++) {
if (eles[i].equals(t)){
return i;
}
}
return -1;
}
//打印当前线性表的元素
public void showEles(){
for (int i = 0; i < N; i++) {
System.out.print(eles[i]+" ");
}
System.out.println();
}
@Override
public Iterator iterator() {
return new SIterator();
}
private class SIterator implements Iterator{
private int cur;
public SIterator(){
this.cur=0;
}
@Override
public boolean hasNext() {
return cur<N;
}
@Override
public T next() {
return eles[cur++];
}
}
}
//测试代码
public class Test {
public static void main(String[] args) throws Exception {
SequenceList<String> squence = new SequenceList<>(5);
//测试遍历
squence.insert(0, "姚明");
squence.insert(1, "科比");
squence.insert(2, "麦迪");
squence.insert(3, "艾佛森");
squence.insert(4, "卡特");
for (String s : squence) {
System.out.println(s);
}
}
}
在之前的实现中,当我们使用 SequenceList时,先new SequenceList(5)创建一个对象,创建对象时就需要指定容器的大小,初始化指定大小的数组来存储元素,当我们插入元素时,如果已经插入了5个元素,还要继续插入数据,则会报错,就不能插入了。这种设计不符合容器的设计理念,因此我们在设计顺序表时,应该考虑它的容量的伸缩性。
考虑容器的容量伸缩性,其实就是改变存储数据元素的数组的大小,那我们需要考虑什么时候需要改变数组的大小?
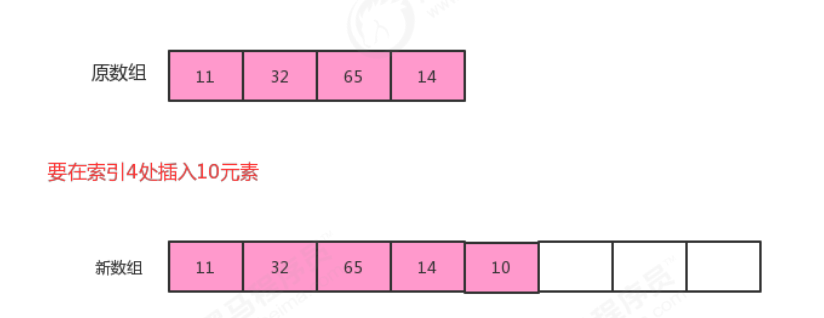
1.添加元素时:
添加元素时,应该检查当前数组的大小是否能容纳新的元素,如果不能容纳,则需要创建新的容量更大的数组,我们这里创建一个是原数组两倍容量的新数组存储元素。
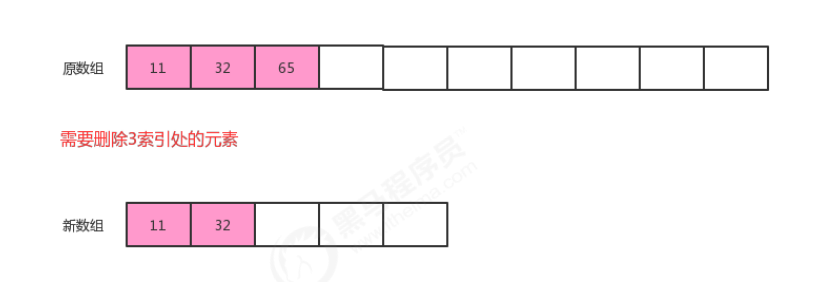
移除元素时,应该检查当前数组的大小是否太大,比如正在用100个容量的数组存储10个元素,这样就会造成内存空间的浪费,应该创建一个容量更小的数组存储元素。如果我们发现数据元素的数量不足数组容量的1/4,则创建一个是原数组容量的1/2的新数组存储元素。
顺序表的容量可变代码:
// 顺序表代码
public class SequenceList<T> implements Iterable<T>{
//存储元素的数组
private T[] eles;
//记录当前顺序表中的元素个数
private int N;
//构造方法
public SequenceList(int capacity){
eles = (T[])new Object[capacity];
N=0;
}
//将一个线性表置为空表
public void clear(){
N=0;
}
//判断当前线性表是否为空表
public boolean isEmpty(){
return N==0;
}
//获取线性表的长度
public int length(){
return N;
}
//获取指定位置的元素
public T get(int i){
if (i<0 || i>=N){
throw new RuntimeException("当前元素不存在!");
}
return eles[i];
}
//向线型表中添加元素t
public void insert(T t){
if (N==eles.length){
resize(eles.length*2);
}
eles[N++] = t;
}
//在i元素处插入元素t
public void insert(int i,T t){
if (i<0 || i>N){
throw new RuntimeException("插入的位置不合法");
}
//元素已经放满了数组,需要扩容
if (N==eles.length){
resize(eles.length*2);
}
//把i位置空出来,i位置及其后面的元素依次向后移动一位
for (int index=N-1;index>i;index--){
eles[index]=eles[index-1];
}
//把t放到i位置处
eles[i]=t;
//元素数量+1
N++;
}
//删除指定位置i处的元素,并返回该元素
public T remove(int i){
if (i<0 || i>N-1){
throw new RuntimeException("当前要删除的元素不存在");
}
//记录i位置处的元素
T result = eles[i];
//把i位置后面的元素都向前移动一位
for (int index=i;index<N-1;index++){
eles[index]=eles[index+1];
}
//当前元素数量-1
N--;
//当元素已经不足数组大小的1/4,则重置数组的大小
if (N>0 && N<eles.length/4){
resize(eles.length/2);
}
return result;
}
//查找t元素第一次出现的位置
public int indexOf(T t){
if(t==null){
throw new RuntimeException("查找的元素不合法");
}
for (int i = 0; i < N; i++) {
if (eles[i].equals(t)){
return i;
}
}
return -1;
}
//打印当前线性表的元素
public void showEles(){
for (int i = 0; i < N; i++) {
System.out.print(eles[i]+" ");
}
System.out.println();
}
@Override
public Iterator iterator() {
return new SIterator();
}
private class SIterator implements Iterator{
private int cur;
public SIterator(){
this.cur=0;
}
@Override
public boolean hasNext() {
return cur<N;
}
@Override
public T next() {
return eles[cur++];
}
}
//改变容量
private void resize(int newSize){
//记录旧数组
T[] temp = eles;
//创建新数组
eles = (T[]) new Object[newSize];
//把旧数组中的元素拷贝到新数组
for (int i = 0; i < N; i++) {
eles[i] = temp[i];
}
}
public int capacity(){
return eles.length;
}
}
//测试代码
public class Test {
public static void main(String[] args) throws Exception {
SequenceList<String> squence = new SequenceList<>(5);
//测试遍历
squence.insert(0, "姚明");
squence.insert(1, "科比");
squence.insert(2, "麦迪");
squence.insert(3, "艾佛森");
squence.insert(4, "卡特");
System.out.println(squence.capacity());
squence.insert(5,"aa");
System.out.println(squence.capacity());
squence.insert(5,"aa");
squence.insert(5,"aa");
squence.insert(5,"aa");
squence.insert(5,"aa");
squence.insert(5,"aa");
System.out.println(squence.capacity());
squence.remove(1);
squence.remove(1);
squence.remove(1);
squence.remove(1);
squence.remove(1);
squence.remove(1);
squence.remove(1);
System.out.println(squence.capacity());
}
}
get(i):不难看出,不论数据元素量N有多大,只需要一次eles[i]就可以获取到对应的元素,所以时间复杂度为O(1);
insert(int i,T t):每一次插入,都需要把i位置后面的元素移动一次,随着元素数量N的增大,移动的元素也越多,时间复杂为O(n);
remove(int i):每一次删除,都需要把i位置后面的元素移动一次,随着数据量N的增大,移动的元素也越多,时间复杂度为O(n);
由于顺序表的底层由数组实现,数组的长度是固定的,所以在操作的过程中涉及到了容器扩容操作。这样会导致顺序表在使用过程中的时间复杂度不是线性的,在某些需要扩容的结点处,耗时会突增,尤其是元素越多,这个问题越明显
java中ArrayList集合的底层也是一种顺序表,使用数组实现,同样提供了增删改查以及扩容等功能。
1.是否用数组实现;
2.有没有扩容操作;
3.有没有提供遍历方式;
之前我们已经使用顺序存储结构实现了线性表,我们会发现虽然顺序表的查询很快,时间复杂度为O(1),但是增删的效率是比较低的,因为每一次增删操作都伴随着大量的数据元素移动。这个问题有没有解决方案呢?有,我们可以使用另外一种存储结构实现线性表,链式存储结构。
链表是一种物理存储单元上非连续、非顺序的存储结构,其物理结构不能只管的表示数据元素的逻辑顺序,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列的结点(链表中的每一个元素称为结点)组成,结点可以在运行时动态生成。
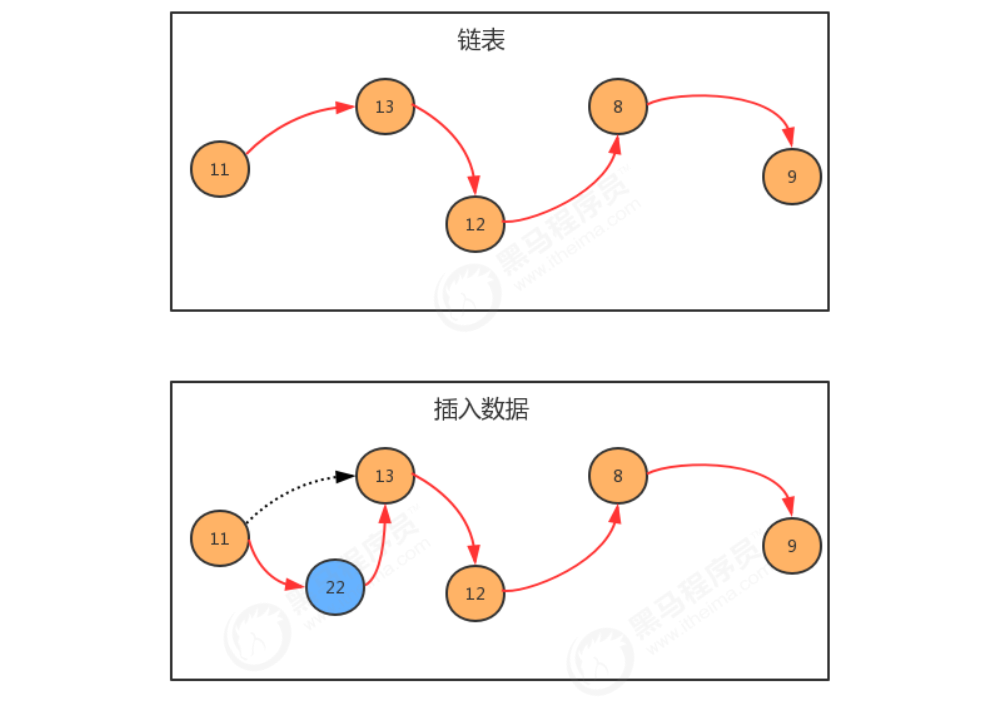
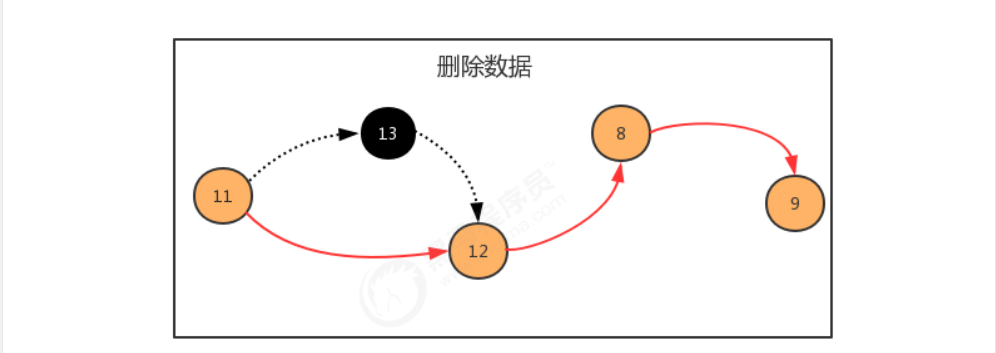
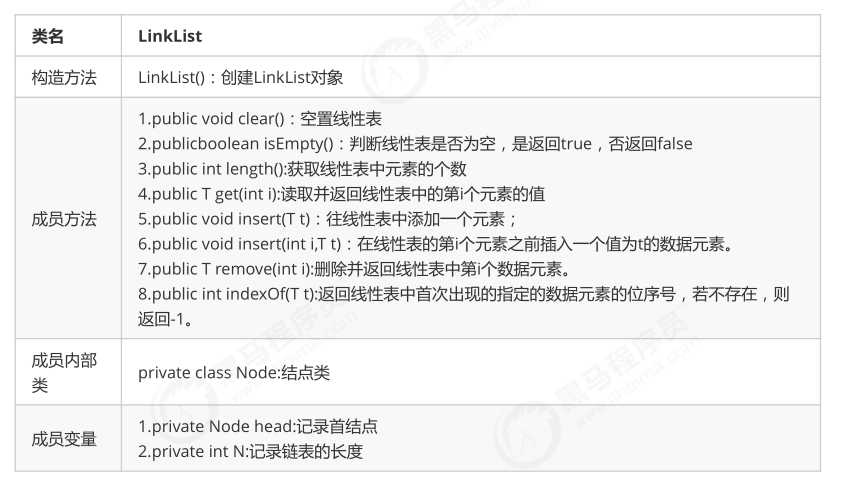
结点API设计:

结点类实现:
public class Node<T> {
//存储元素
public T item;
//指向下一个结点
public Node next;
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
生成链表:
public static void main(String[] args) throws Exception {
//构建结点
Node<Integer> first = new Node<Integer>(11, null);
Node<Integer> second = new Node<Integer>(13, null);
Node<Integer> third = new Node<Integer>(12, null);
Node<Integer> fourth = new Node<Integer>(8, null);
Node<Integer> fifth = new Node<Integer>(9, null);
//生成链表
first.next = second;
second.next = third;
third.next = fourth;
fourth.next = fifth;
}
单向链表是链表的一种,它由多个结点组成,每个结点都由一个数据域和一个指针域组成,数据域用来存储数据,指针域用来指向其后继结点。链表的头结点的数据域不存储数据,指针域指向第一个真正存储数据的结点。

// 单向列表代码
import java.util.Iterator;
public class LinkList<T> implements Iterable<T> {
//记录头结点
private Node head;
//记录链表的长度
private int N;
public LinkList(){
//初始化头结点
head = new Node(null,null);
N=0;
}
//清空链表
public void clear(){
head.next=null;
head.item=null;
N=0;
}
//获取链表的长度
public int length(){
return N;
}
//判断链表是否为空
public boolean isEmpty(){
return N==0;
}
//获取指定位置i出的元素
public T get(int i){
if (i<0||i>=N){
throw new RuntimeException("位置不合法!");
}
Node n = head.next;
for (int index = 0; index < i; index++) {
n = n.next;
}
return n.item;
}
//向链表中添加元素t
public void insert(T t){
//找到最后一个节点
Node n = head;
while(n.next!=null){
n = n.next;
}
Node newNode = new Node(t, null);
n.next = newNode;
//链表长度+1
N++;
}
//向指定位置i处,添加元素t
public void insert(int i,T t){
if (i<0||i>=N){
throw new RuntimeException("位置不合法!");
}
//寻找位置i之前的结点
Node pre = head;
for (int index = 0; index <=i-1; index++) {
pre = pre.next;
}
//位置i的结点
Node curr = pre.next;
//构建新的结点,让新结点指向位置i的结点
Node newNode = new Node(t, curr);
//让之前的结点指向新结点
pre.next = newNode;
//长度+1
N++;
}
//删除指定位置i处的元素,并返回被删除的元素
public T remove(int i){
if (i<0 || i>=N){
throw new RuntimeException("位置不合法");
}
//寻找i之前的元素
Node pre = head;
for (int index = 0; index <=i-1; index++) {
pre = pre.next;
}
//当前i位置的结点
Node curr = pre.next;
//前一个结点指向下一个结点,删除当前结点
pre.next = curr.next;
//长度-1
N--;
return curr.item;
}
//查找元素t在链表中第一次出现的位置
public int indexOf(T t){
Node n = head;
for (int i = 0;n.next!=null;i++){
n = n.next;
if (n.item.equals(t)){
return i;
}
}
return -1;
}
//结点类
private class Node{
//存储数据
T item;
//下一个结点
Node next;
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
@Override
public Iterator iterator() {
return new LIterator();
}
private class LIterator implements Iterator<T>{
private Node n;
public LIterator() {
this.n = head;
}
@Override
public boolean hasNext() {
return n.next!=null;
}
@Override
public T next() {
n = n.next;
return n.item;
}
}
}
//测试代码
public class Test {
public static void main(String[] args) throws Exception {
LinkList<String> list = new LinkList<>();
list.insert(0,"张三");
list.insert(1,"李四");
list.insert(2,"王五");
list.insert(3,"赵六");
//测试length方法
for (String s : list) {
System.out.println(s);
}
System.out.println(list.length());
System.out.println("-------------------");
//测试get方法
System.out.println(list.get(2));
System.out.println("------------------------");
//测试remove方法
String remove = list.remove(1);
System.out.println(remove);
System.out.println(list.length());
System.out.println("----------------");;
for (String s : list) {
System.out.println(s);
}
}
}
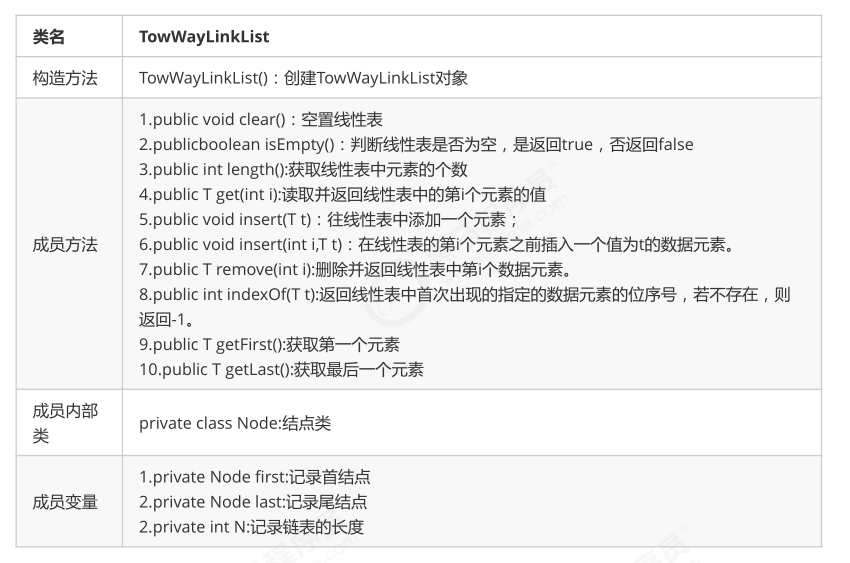
双向链表也叫双向表,是链表的一种,它由多个结点组成,每个结点都由一个数据域和两个指针域组成,数据域用来存储数据,其中一个指针域用来指向其后继结点,另一个指针域用来指向前驱结点。链表的头结点的数据域不存储数据,指向前驱结点的指针域值为null,指向后继结点的指针域指向第一个真正存储数据的结点。
按照面向对象的思想,我们需要设计一个类,来描述结点这个事物。由于结点是属于链表的,所以我们把结点类作为链表类的一个内部类来实现

// 双向链表代码
import java.util.Iterator;
public class TowWayLinkList<T> implements Iterable<T>{
//首结点
private Node head;
//最后一个结点
private Node last;
//链表的长度
private int N;
public TowWayLinkList() {
last = null;
head = new Node(null,null,null);
N=0;
}
//清空链表
public void clear(){
last=null;
head.next=last;
head.pre=null;
head.item=null;
N=0;
}
//获取链表长度
public int length(){
return N;
}
//判断链表是否为空
public boolean isEmpty(){
return N==0;
}
//插入元素t
public void insert(T t){
if (last==null){
last = new Node(t,head,null);
head.next = last;
}else{
Node oldLast = last;
Node node = new Node(t, oldLast, null);
oldLast.next = node;
last = node;
}
//长度+1
N++;
}
//向指定位置i处插入元素t
public void insert(int i,T t){
if (i<0 || i>=N){
throw new RuntimeException("位置不合法");
}
//找到位置i的前一个结点
Node pre = head;
for (int index = 0; index < i; index++) {
pre = pre.next;
}
//当前结点
Node curr = pre.next;
//构建新结点
Node newNode = new Node(t, pre, curr);
curr.pre= newNode;
pre.next = newNode;
//长度+1
N++;
}
//获取指定位置i处的元素
public T get(int i){
if (i<0||i>=N){
throw new RuntimeException("位置不合法");
}
//寻找当前结点
Node curr = head.next;
for (int index = 0; index <i; index++) {
curr = curr.next;
}
return curr.item;
}
//找到元素t在链表中第一次出现的位置
public int indexOf(T t){
Node n= head;
for (int i=0;n.next!=null;i++){
n = n.next;
if (n.next.equals(t)){
return i;
}
}
return -1;
}
//删除位置i处的元素,并返回该元素
public T remove(int i){
if (i<0 || i>=N){
throw new RuntimeException("位置不合法");
}
//寻找i位置的前一个元素
Node pre = head;
for (int index = 0; index <i ; index++) {
pre = pre.next;
}
//i位置的元素
Node curr = pre.next;
//i位置的下一个元素
Node curr_next = curr.next;
pre.next = curr_next;
curr_next.pre = pre;
//长度-1;
N--;
return curr.item;
}
//获取第一个元素
public T getFirst(){
if (isEmpty()){
return null;
}
return head.next.item;
}
//获取最后一个元素
public T getLast(){
if (isEmpty()){
return null;
}
return last.item;
}
@Override
public Iterator<T> iterator() {
return new TIterator();
}
private class TIterator implements Iterator{
private Node n = head;
@Override
public boolean hasNext() {
return n.next!=null;
}
@Override
public Object next() {
n = n.next;
return n.item;
}
}
//结点类
private class Node{
public Node(T item, Node pre, Node next) {
this.item = item;
this.pre = pre;
this.next = next;
}
//存储数据
public T item;
//指向上一个结点
public Node pre;
//指向下一个结点
public Node next;
}
}
//测试代码
public class Test {
public static void main(String[] args) throws Exception {
TowWayLinkList<String> list = new TowWayLinkList<>();
list.insert("乔峰");
list.insert("虚竹");
list.insert("段誉");
list.insert(1,"鸠摩智");
list.insert(3,"叶二娘");
for (String str : list) {
System.out.println(str);
}
System.out.println("----------------------");
String tow = list.get(2);
System.out.println(tow);
System.out.println("-------------------------");
String remove = list.remove(3);
System.out.println(remove);
System.out.println(list.length());
System.out.println("--------------------");
System.out.println(list.getFirst());
System.out.println(list.getLast());
}
}
java中LinkedList集合也是使用双向链表实现,并提供了增删改查等相关方法
1.底层是否用双向链表实现;
2.结点类是否有三个域
get(int i):每一次查询,都需要从链表的头部开始,依次向后查找,随着数据元素N的增多,比较的元素越多,时间复杂度为O(n)
insert(int i,T t):每一次插入,需要先找到i位置的前一个元素,然后完成插入操作,随着数据元素N的增多,查找的元素越多,时间复杂度为O(n);
remove(int i):每一次移除,需要先找到i位置的前一个元素,然后完成插入操作,随着数据元素N的增多,查找的元素越多,时间复杂度为O(n)
相比较顺序表,链表插入和删除的时间复杂度虽然一样,但仍然有很大的优势,因为链表的物理地址是不连续的,它不需要预先指定存储空间大小,或者在存储过程中涉及到扩容等操作,,同时它并没有涉及的元素的交换。
相比较顺序表,链表的查询操作性能会比较低。因此,如果我们的程序中查询操作比较多,建议使用顺序表,增删操作比较多,建议使用链表。
单链表的反转,是面试中的一个高频题目。
需求:
原链表中数据为:1->2->3>4
反转后链表中数据为: 4->3->2->1
反转API:
public void reverse() :对整个链表反转
public Node reverse(Node curr) :反转链表中的某个结点curr,并把反转后的curr结点返回
使用递归可以完成反转,递归反转其实就是从原链表的第一个存数据的结点开始,依次递归调用反转每一个结点,
直到把最后一个结点反转完毕,整个链表就反转完毕。
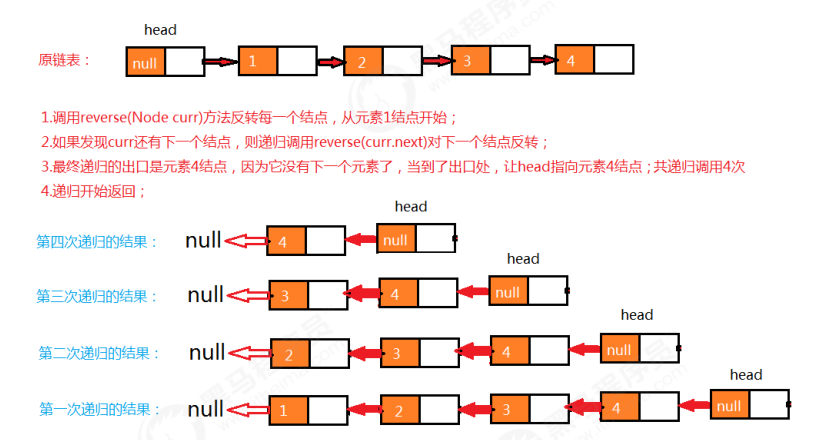
代码 :
原文:https://www.cnblogs.com/tianwenxin/p/14235779.html