图由顶点集和边集组成,记为G=(V,E)
1、邻接矩阵。用一个一维数组存储图中的顶点信息,用一个二维数组存储边的信息。
图的临界矩阵存储结构定义
typedef char vertexType[10]; //vertexType a; sizeof(a) = 10; #define MAX 50 //最大顶点数 typedef struct { vertexType vertex[MAX]; //顶点数组 int edge[MAX][MAX];//边表 int vertexNum; //顶点个数 int edgeNum; //边的个数 }Graph;
创建一个无向图
//求用户输入的顶点在顶点数组的位置 int LocateVertex(Graph &g, vertexType v) { for (size_t i = 0; i < g.vertexNum; ++i) { if (strcmp(v, g.vertex[i]) == 0) return i; } return -1; } void CreateGraph(Graph &g) { cout << "请输入图中的顶点数和边数" << endl; cin >> g.vertexNum >> g.edgeNum; cout << "请输入" << g.vertexNum << "个顶点数的值" << endl; for (size_t i = 0; i < g.vertexNum; i++) { cin >> g.vertex[i]; //把输入的顶点存储在顶点数组中 } //初始化矩阵为0 for (size_t i = 0; i < g.vertexNum; i++) { for (size_t j = 0; j < g.vertexNum; j++) { g.edge[i][j] = 0; } } //如果v0和v1之间有边输入 v0 v1 //如果v2和v4之间有边输入 v2 v4 cout << "请输入" << g.edgeNum << "条边的两个顶点" << endl; vertexType v1, v2; //相当于char v1[10] char v2[10] for (size_t i = 0; i < g.edgeNum; i++) { cin >> v1 >> v2 ; //用户输入的顶点在顶点数组中的位置 int m = LocateVertex(g, v1); int n = LocateVertex(g, v2); //边对应的二维数组赋值 g.edge[m][n] = 1; g.edge[n][m] = 1; } }
2、邻接表。对图中的每个顶点vi建立一条单链表,第i个单链表中的结点表示依附于顶点vi的边。这个单链表就称为顶点vi的边表。边表的头指针和顶点的数据采用顺序存储。
邻接表的存储结构
//边表 struct edgeNode{ int position; //当前顶点在顶点数组中的位置 struct edgeNode * next; }; //顶点表结构 struct vertex { char name[9]; struct edgeNode * first; //边表头指针 }; struct GraphList { vertex head[MAX]; //顶点表数组 int vertexNum; //顶点数 int edgeNum; //边数 };
创建图
void CreateGraph(GraphList &g) { cout << "请输入图的顶点数和边数" << endl; cin >> g.vertexNum >> g.edgeNum; cout << "输入" << g.vertexNum << "个顶点的值" << endl; for (size_t i = 0; i < g.vertexNum; i++) { cin >> g.head[i].name; g.head[i].first = NULL; //头指针置为空 } cout << "请输入边的两个顶点" << endl; char v1[9], v2[9]; for (size_t i = 0; i < g.edgeNum; i++) { cin >> v1 >> v2; //输入的顶点在数组中的位置 int m = LocateVertex(g, v1); int n = LocateVertex(g, v2); //链表中添加邻接点 edgeNode * pNew = new edgeNode; pNew->position = n; //头插法 pNew->next = g.head[m].first; g.head[m].first = pNew; #if 1 //无向图返过来 edgeNode * pNew1 = new edgeNode; pNew1->position = m; pNew1->next = g.head[n].first; g.head[n].first = pNew1; #endif; } }
1、深度优先遍历(DFS)
类似于树的先序遍历。首先访问某一个起始位置V,由V出发,访问与V相邻但未被访问的任意一个顶点W,再访问W邻接但没有被访问的顶点......重复以上过程。当不能在访问时,依次退回最近一个被访问的顶点,如果他有邻接点但是未被访问,从这个顶点开始继续上述搜索过程。直到所有的顶点都被访问完为止。
void DFS(Graph &g) { //一个标记数组,用来标记是否被访问,初始化为false, bool * visit = new bool[g.vertexNum]; for (size_t i = 0; i < g.vertexNum; i++) { visit[i] = false; } stack<int> s; visit[0] = true; //标记 cout << g.vertex[0] << " "; //访问 s.push(0); //入栈 while (!s.empty()) { for (size_t i = 0; i < g.vertexNum; i++) { int top = s.top(); if (!visit[i] && g.edge[top][i]>0) //有邻接点,且顶点未被访问 { visit[i] = true; //标记 cout << g.vertex[i] << " "; //访问 s.push(i); //入栈 } } s.pop(); //不能继续访问,退回到最近访问的顶点 } delete[] visit; }
2、广度优先遍历(BFS)
访问起始顶点V,由V出发访问V的各个未被访问的所有邻接点w1,w2,w3.......,然后访问w1,w2,w3....的所有未被访问的顶点,依次类推。
void BFS(Graph &g) { bool *visit = new bool[g.vertexNum]; for (size_t i = 0; i < g.vertexNum; i++) { visit[i] = false; } queue<int>q; visit[0] = true; cout << g.vertex[0] << " "; q.push(0); //入队 while (!q.empty()) { int front = q.front(); for (size_t i = 0; i < g.vertexNum; i++) { if (!visit[i] && g.edge[front][i]>0) //访问与该顶点邻接但未被访问的所有顶点 { visit[i] = true; cout << g.vertex[i] << " "; q.push(i); } } q.pop(); //出队 } delete[] visit; }
最短路径问题(迪杰斯特拉算法)
当图是带权图时,把从一个顶点v0到图中任意一个顶点vi的一个路径,可能不止一条,所经过边上的权值之和,定义为该路径的带权路径长度,其中最短的那条路径为最短路径。
该算法需要三个辅助数组,S[]记录已经求得的最短路径的顶点,dist[]记录从源点到其余各点的当前最短路径长度,path[]:path[i]表示到顶点i的最短路径的前驱结点。
步骤:1、初始化集合S[]为0,当有一个顶点计算完成,将对应的下标的值改为1;
2、初始化数组dist[],记录从源点到其他各个顶点当前的最短路径长度,从中选出最小的那个j,将j加入到S集合中。
3、修改从源点出发到任意一个顶点vk可达的最短路径长度:如果dist[j]+arcs[j][k]<dist[k]则令dist[k]=dist[j]+arcs[j][k]
4、重复以上动作
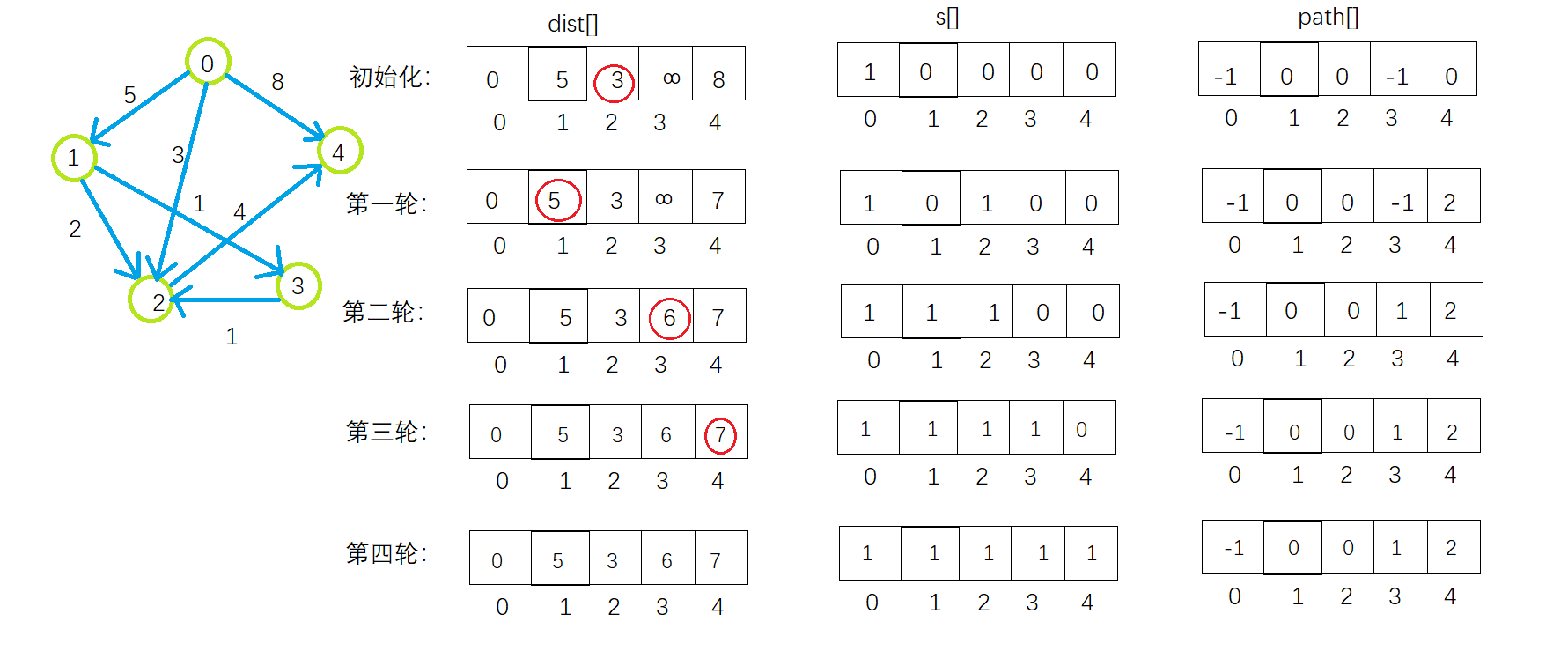
int * Dijkstra(Graph g, int v) { //==================初始化===================== int s[MAXVERTEX];//标记数组,表示当前有哪些顶点加入 int path[MAXVERTEX];//最短路径中顶点的前驱顶点 int dis[MAXVERTEX];//从原点出发,到各个顶点的最短路径 for (int i = 0; i < g.vertexNum; ++i) { dis[i] = g.edge[v][i]; s[i] = 0; if (g.edge[v][i] < MAXNUM) path[i] = v; else { path[i] = -1; } } path[v] = -1; s[v] = 1; //原点加入 //============初始化完成======================== for (int i = 0; i < g.vertexNum; ++i) { //找dis数组中最小的值 int min = MAXNUM; int u;//记录最小值的顶点 for (size_t j = 0; j < g.vertexNum; j++) { if (dis[j] < min) { min = dis[j]; u = j; } } s[u] = 1; //加入进来 for (int j = 0; j < g.vertexNum; ++j) { if (s[j] == 0 && dis[u] + g.vertex[u][j] < dis[j]) { dis[j] = dis[u] + g.vertex[u][j]; path[j] = u; //修改path表明到j顶点的前一个顶点是u } } } return path; }
void showpath(Graph &g, int *path, int v0, int v) { stack<int>s; int temp = v; while (temp!=v0) { s.push(temp); temp = path[temp]; } while (!s.empty()) { cout << g.vertex[s.top()] << "--->"; s.pop(); } }
原文:https://www.cnblogs.com/xiaoxiaolinux/p/14238320.html