区间问题

问题如下：

解题思路：

这道题也是贪心算法的经典问题。同样，在使用贪心算法之前，我们应该找到这道题的贪心策略。这道题不像之前的硬币问题那么简单，我们可以设计出各种各样的贪心策略。具体如下：

• 在可选的工作（也就是和目前已经选的工作都不重叠的工作）中，每次都选取开始时间最早的工作。
• 在可选的工作中，每次都选取结束时间最早的工作。
• 在可选的工作中，每次都选取用时最短的工作。
• 在可选的工作中，每次都选与最少可选工作有重叠的工作。
  
  

在以上贪心策略中，只有第二点是可以进行求解的。在其它的贪心策略中，我们都能找到其相应的反例：

对于第一种：

对于第三种：

对于第四种：（在第四种的反例中，最少可选工作为两个)

因此从以上的结论我们可以看出：要想使用贪心算法，那么贪心策略的正确性就显得尤其重要。如果你的贪心策略是错误的话，那么你的算法也就是错误的。因此，在使用贪心算法时，一定要注意如何去构建正确的贪心策略。

那么在这个问题当中，只有第二种的贪心策略是可以进行求解的。

代码如下：

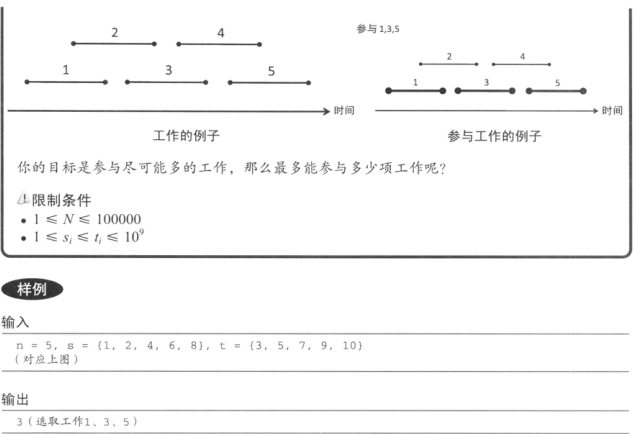
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int Start[100000];                //定义存储开始时间的数组
int End[100000];                  //定义存储结束时间的数组
pair<int, int> works[100000];     //用于存储工作的pair数组
int N;                            //N代表一共有多少项工作
int main() {
	int i;
	int sum = 0;                  //代表选取工作的总数
	int t = 0;                    //t代表当前所选工作的结束时间（默认为0）
	scanf("%d", &N);
	for (i = 0; i < N; i++) {
		scanf("%d", &Start[i]);   //进行开始时间的赋值
	}
	for (i = 0; i < N; i++) {
		scanf("%d", &End[i]);     //进行结束时间的赋值
	}
	for (i = 0; i < N; i++) {
		works[i] = make_pair(End[i], Start[i]);     //因为这里贪心策略需要选择结束时间最早的可选工作，又因为pair数对是按照first排序，所以我们让结束时间放在first中,让开始时间放在second中。     
	}
	sort(works, works + N);       //在所有的工作中进行结束时间的排序（从小到大，因为我们要选择结束时间最早的可选工作）

	for (i = 0; i < N; i++) {
		if (t < works[i].second) {    //如果所遍历工作的起始时间，比当前所选工作的结束时间大，那么该工作就可选，否则不可选。
			sum++;                    //工作选完之后，选取工作的总数+1
			t = works[i].first;       //t等于当前所选工作的结束时间
		}
	}
	cout << sum << endl;
}

执行结果：

区间问题

原文：https://www.cnblogs.com/gao79135/p/14250834.html