前提知识:
一个\(\vec{a}\)如下图所示:
\(\vec{a} = \left[
\begin{matrix}
x_a\ y_b\ \end{matrix}
\right]\), \(\vec{b} = \left[
\begin{matrix}
x_c\ y_d\ \end{matrix}
\right]\)
\(||\vec{a}||\)表示\(\vec{a}\)的长度,\(||\vec{b}||\)表示\(\vec{b}\)的长度。
\(||\vec{a}|| = \sqrt{x_a^2 + y_b^2},||\vec{b}|| = \sqrt{x_c^2 + y_d^2}\)
点乘的计算公式:
\(\vec{a} \cdot \vec{b} = ||\vec{a}|| ||\vec{b}|| cos\theta = x_ax_c+y_by_d\)
\(\theta\)角为\(\vec{a}\)和\(\vec{b}\)的夹角
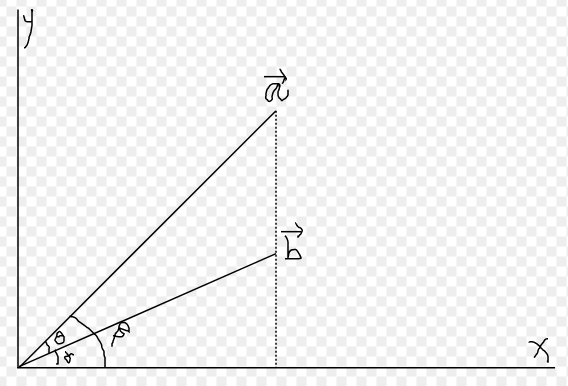
推导:\(||\vec{a}|| ||\vec{b}|| cos\theta = x_ax_c+y_by_d\)
- 由上图可知,\(\theta = \beta - \alpha\)
- 所以,\(cos\theta = cos(\beta - \alpha)\)
- 由三角函数公式可知:\(cos\theta = cos\beta cos\alpha + sin\alpha sin\beta\)
- 观察上图后可知,\(cos\beta = {x_a\over||\vec{a}||}\),\(sin\beta = {y_b\over||\vec{a}||}\),\(cos\alpha = {x_c\over||\vec{b}||}\),\(sin\alpha = {y_d\over||\vec{b}||}\)
- 所以,\(cos\theta = {x_ax_c+y_by_d \over ||\vec{a}|| ||\vec{b}||}\)
- 所以,\(||\vec{a}|| ||\vec{b}|| cos\theta = x_ax_c+y_by_d\)
向量点乘的推导
原文:https://www.cnblogs.com/sf5803/p/14252625.html

