用二项式定理展开,把同类项合并到一起,差不多就是这样:
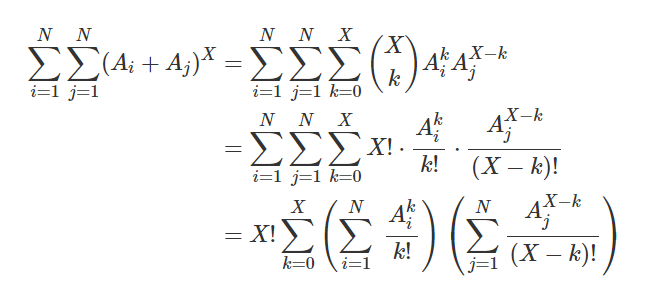
把两个括号内分别计算再相乘
#include <bits/stdc++.h>
using namespace std;
#define int long long
void read (int &x) {
char ch = getchar(); x = 0; while (!isdigit(ch)) ch = getchar();
while (isdigit(ch)) x = x * 10 + ch - 48, ch = getchar();
} const int N = 2e5 + 5, mod = 998244353;
int n, m, a[N], b[N], pw[350], in[350], sum[305];
int qpow (int x, int y) {
int t = 1;
while (y) {
if (y & 1) t = t * x % mod;
x = x * x % mod, y >>= 1;
} return t;
}
signed main() {
read (n), read (m); pw[0] = in[0] = 1;
for (int i = 1; i <= n; ++i) read (a[i]);
for (int i = 1; i <= m; ++i)
pw[i] = pw[i - 1] * i % mod, in[i] = qpow (pw[i], mod - 2);
for (int i = 1; i <= n; ++i)
for (int j = 0, t = 1; j <= m; ++j, t = t * a[i] % mod)
sum[j] = (sum[j] + t * in[j]) % mod;
for (int i = 1; i <= n; ++i) a[i] += a[i], b[i] = a[i];
int inv = qpow (2, mod - 2);
for (int i = 1; i <= m; ++i) {
int res = 0;
for (int j = 0; j <= i; ++j)
res = (res + sum[j] * sum[i - j]) % mod;
res *= pw[i]; for (int j = 1; j <= n; ++j) res -= a[j]; res = res % mod + mod;
printf ("%lld\n", res * inv % mod);
for (int j = 1; j <= n; ++j) a[j] = a[j] * b[j] % mod;
}
return 0;
}
容易想到二分答案,可以得出答案上界是 \(2\times n \times k\)
判定可行的方式比较奇怪,用到了 Hall定理 ,把每个人得到每块奖牌看作二分图的左部点,共 \(n\times k\) 个,把每一天看作右部点。如果第 \(i\) 个人在第 \(j\) 天上班,把 \(i\) 的 \(k\) 个点都和 \(j\) 连一条边
但边数很多,不能直接搞。根据 \(hall\) 定理,左部点的每个子集 \(A\) 连向的右部点子集的大小 \(P(A)\),要满足 \(| A|\leq|P(A)|\)。先考虑同一个人 \(i\) 的 \(k\) 个点,这些点连向的点集 \(S(i)\)相同,只要判断一下 \(k\leq |S(i)|\),然后可以把 \(k\) 个点看成一个
不同的人组成的点集,共有 \(2^n\) 种情况。把每一天哪些人来上班用二进制表示。如果某一天的上班情况用二进制表示为 \(Q\),\(Q_i\) 表示二进制下第 \(i\) 位(第 \(i\) 个人上班否)。\(Q\) 对哪些组合有贡献呢?显然是二进制表示下和 \(Q\) 有重合的点集。但这个似乎不好算,可以反过来,把所有点集 \(+1\),然后没有重合的 \(-1\),用 \(fwt\) 计算 \(-1\) 的过程
#include <bits/stdc++.h>
using namespace std;
#define int long long
void read (int &x) {
char ch = getchar(); x = 0; while (!isdigit(ch)) ch = getchar();
while (isdigit(ch)) x = x * 10 + ch - 48, ch = getchar();
} const int N = 18, M = 1e5 + 5;
int n, k, res, d[N], a[1 << N], c[1 << N], p[2 * N * M];
int check (int t) {
memset (a, 0, sizeof (a));
for (int i = 1; i <= t; ++i) ++a[p[i]];
int mx = 1 << n;
for (int i = 1; i < mx; i <<= 1)
for (int j = 0; j < mx; j += (i << 1))
for (int k = 0; k < i; ++k) a[j | k] += a[j | k | i];
for (int i = mx - 1; i >= 1; --i)
if (c[i] * k > t - a[i]) return 0; return 1;
}
signed main() {
read (n), read (k);
for (int i = 1; i <= n; ++i) read (d[i]);
c[0] = 0;
for (int i = 1; i < (1 << n); ++i)
c[i] = c[i >> 1] + (i & 1);
for (int i = 1, qwq; i <= 2 * n * k; ++i) {
p[i] = (1 << n) - 1;
for (int j = 1; j <= n; ++j) {
qwq = i % (d[j] << 1);
if (qwq && qwq <= d[j]) p[i] ^= (1 << j - 1);
}
}
int l = 1, r = 2 * n * k, res = r;
while (l <= r) {
int mid = l + r >> 1;
if (check (mid)) res = mid, r = mid - 1;
else l = mid + 1;
}
return printf ("%lld\n", res), 0;
}
思路巧妙但容易理解的计数问题。
首先,要保证图连通,不难发现,充要条件是每个 \(Part\) 都至少使用一个接口。先把这些接口都选了,这是答案的第一部分
然后,一共使用 \(2n-2\) 个接口,还剩 \(n-2\) 个要选,奇妙的事情发生了
把剩下的所有接口放在一起,假设一共 \(S\) 个,从中选 \(n-2\) 个的排列数就是答案的第二部分。\(But...Why???\)
其实就是要证明一个排列和一种接法一一对应(这里的排列包括第一部分从每个 \(Part\) 选的一个接口)对应方法:从左向右扫描整个排列,如果当前接口已经标记过,跳过;否则,从右边选一个最近的,在不同 Part 上的接口作为边的另一端。这样就和接法对应上了,并且可以发现改变排列的顺序也会改变连边方案。
#include <bits/stdc++.h>
using namespace std;
#define int long long
void read (int &x) {
char ch = getchar(); x = 0; while (!isdigit(ch)) ch = getchar();
while (isdigit(ch)) x = x * 10 + ch - 48, ch = getchar();
} const int N = 2e5 + 5, mod = 998244353;
int n, s, res = 1;
signed main() {
read (n);
for (int i = 1, x; i <= n; ++i)
read (x), res = res * x % mod, s += x - 1;
s %= mod;
for (int i = 1; i <= n - 2; ++i)
res = res * (s - i + 1) % mod;
return printf ("%lld\n", res), 0;
}
AtCoder Regular Contest 106 DEF
原文:https://www.cnblogs.com/whx666/p/14279273.html