LeetCode - 寻找两个正序数组的中位数 (No.4)

#4 review

• issue #4 - reference
• idea - reference

#4 details

给定两个大小为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数。

进阶：你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗？

• e.g.1

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

• e.g.2

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

• e.g.3

输入：nums1 = [0,0], nums2 = [0,0]
输出：0.00000

idea

idea gif demo can be checked in idea - reference

1 中位数两边的数量，对于一个序列中位数，分为两种情况来讨论（假设nums1的长度小）：

• nums1和nums2的长度之和为奇数，此时我们将中间分割线取左边元素多一个的位置，此时分割线指针指向的元素为\(\frac{\text{sizeof(nums1)} + \text{sizeof(nums2)} + 1}{2}\)，为防止溢出，代码表示为，

int m = nums1.size();
int n = nums2.size();
int sizeLeft = m + (n - m + 1) / 2;

• nums1和nums2的长度之和为偶数，此时我们取使得左右两边相同元素成立的中线，此时中线指向\(\frac{\text{sizeof(nums1)} + \text{sizeof(nums2)}}{2}\)，由于int向下取整，亦可表示为\(\frac{\text{sizeof(nums1)} + \text{sizeof(nums2)} + 1}{2}\).

2 接着我们考虑用两个指针将nums1和nums2分开，如图，此时中线指针center1和center2分别指向9和12，

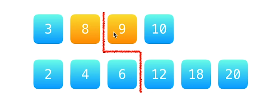
num1的中线指针为center1，此时nums2的指针为center2，可有如下是式子获得，

int center2 = sizeLeft - center1;

3 到此处，我们所需要做的就是确定nums1中线指针所指向的位置，对nums1进行二分查找。

首先分配两个指针，分别初始化指向nums1的首部和尾部，

int i = 0;
int j = m;
int center1 = (i + j + 1) / 2;

遍历过程中考虑两种情况，

• center1所指向的中线左边的元素大于center2右边的元素，此时与我们预想的先验（中线左边的所有元素均小于中心啊右边的所有元素）相悖，我们将cener1更新，即，

if (nums1[center1 - 1] > nums2[center2]) {
    j = center1 - 1;
}

• center2左边的元素大于等于center1右边的元素，此时需要将center1更新，即，

else {
    i = cneter1;
}

遍历完成即可得到最终的结果，其中遍历进行的条件是i < j。

循环过程代码如下,

int i = 0;
int j = m;
while (i < j) {
    if (nums[center1 - 1] > nums2[center2]) {
        j = center1 - 1;
    } else {
        i = center1;
    }
}

4 最后确定中位数，若nums1和nums2总元素之和为奇数，那么结果便是中线左边两个元素的最大取值（此处需考虑指针为0或者为数组最大长度的特殊情况），即

int maxNums1Left = (i == 0) : (INT_MIN) ? (nums1[i - 1]);
int maxNums2Left = ((sizeLeft - i == 0) ? (INT_MIN) : (nums2[sizeLeft - i- 1]);
int ans = max(maxNums1Left, maxNums2Left);

相反，若为偶数，

int minNums1Left = (i == m) ? (INT_MAX) : (nums1[left]);
int minNumsRight = ((sizeLeft - left) == n) ? (INT_MAX) : (nums2[sizeLeft - left]);
return (double) (max(maxNum1Left, maxNum2Left) + min(minNum1Right, minNum2Right)) / 2;

code

class Solution {
public:
    double findMedianSortedArrays(vector<int>& num1, vector<int>& num2) {
        int m = num1.size();
        int n = num2.size();
        if (m > n) {
            return findMedianSortedArrays(num2, num1);
        }
        // 左边的size
        int sizeLeft = m + (n - m + 1) / 2;
        
        int left = 0;
        int right = m;
        while (left < right) {
            int center1 = left + (right - left + 1) / 2;
            int center2 = sizeLeft - center1;
            
            // cout << center1 << "\t" << center2 << endl;
            if (num1[center1 - 1] > num2[center2]) {
                right = center1 - 1;
            } else {
                left = center1;
            }
        }
        // here, 分割线到了合适的位置
        int maxNum1Left = (left == 0) ? (INT_MIN) : (num1[left - 1]);
        int minNum1Right = (left == m) ? (INT_MAX) : (num1[left]);
        int maxNum2Left = ((sizeLeft - left) == 0) ? (INT_MIN) : (num2[(sizeLeft - left) - 1]);
        int minNum2Right = ((sizeLeft - left) == n) ? (INT_MAX) : (num2[sizeLeft - left]);

        if ((m + n)  % 2) {
            return max(maxNum1Left, maxNum2Left);
        } else {
            return (double) (max(maxNum1Left, maxNum2Left) + min(minNum1Right, minNum2Right)) / 2;
        }
    }
};

result

LeetCode - 寻找两个正序数组的中位数 (No.4)

原文：https://www.cnblogs.com/litun/p/letcode_solution_4.html