对于多幅不同角度图像，其拼接过程相较于两幅图像拼接更加复杂，以下给出具体理论模型：
1 3D到2D透视投影
三维空间上点 p 投影到二维空间 q 有两种方式：1）正交投影，2）透视投影。
正交投影直接舍去 z 轴信息，该模型仅在远心镜头上是合理的，或者对于物体深度远小于其到摄像机距离时的近似模型。
常规镜头成像可以使用透视投影建模，如下图：
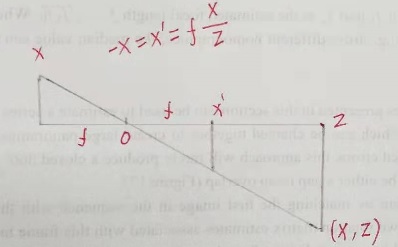
三维空间点 p=(X,Y,Z) 投影到二维空间点 q = (x,y)，镜头光轴在 Z 轴上，满足关系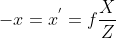 
，
真实的物理模型将 X 投影到 x, 但使用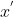 
可以避免关系式中产生一个负号，因此投影点可写为 
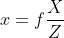, 同理，有 
。
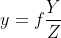使用矩阵可表示为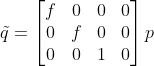 
，变换结果 
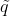为齐次坐标，
。
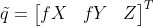以上变换举证前三列可表达相机自身相关性质，被称为内参，比如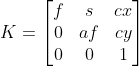 
，其中， f 表示相机焦距，af表示像元横纵比（一般情形下为 1），
cx,cy 表示 CCD 中心与光轴间平移距离，s 表示了 CCD 法向量与光轴不平行程度。
在实际应用中，一般会使用简单模型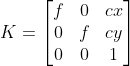 
，该模型仅表达了焦距与CCD中心平移。
如果将以上变换矩阵改写成满秩矩阵，那么其逆变换就变得很简单，使用 4*4 变换矩阵重新构造透视投影如下：
，
，
,
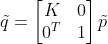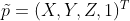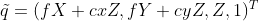改写齐次坐标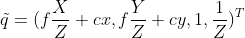 
，前两个分量表示图像上坐标值，第四个分量表示深度信息。
以上透视投影模型要求三维空间坐标满足以下条件：
1）以镜头光心（小孔成像中的小孔）为原点；
2）Z轴垂直与 CCD 平面；
3）XY轴与 CCD 平面 xy 轴平行；
但在实际三维坐标系可能是任意建立的，所以在透视投影前需要变换坐标系，使用平移+旋转模型如下：
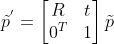，其中，R 为 3*3 旋转矩阵，t 为平移向量。
综上，任意三维空间上点到二维平面的透视投影可表示为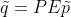 
，
，
。
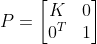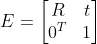2 图像配准
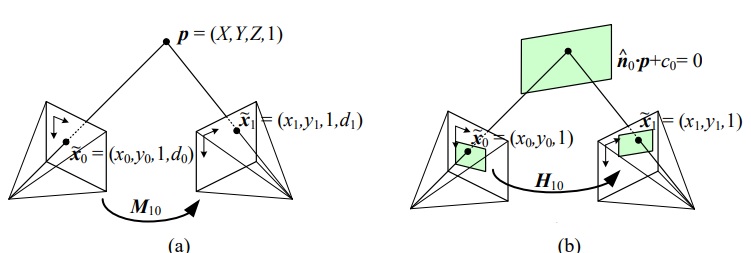
如上图(a)所示，三维空间上点 p 映射到图像平面为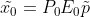 
，由于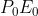 
均为满足矩阵，故其逆矩阵一定存在，有 
。
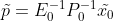结合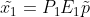 
可建立 
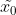与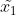 
之间的关系为 
。
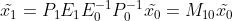以上关系需要相机记录成像点深度信息，一般相机无法记录深度信息，因此，可以使用图像 (b)建立关系：
假设所有三维空间上点均在一个空间平面上，即满足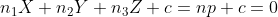 
，
当进行投影变换时，其深度信息为零, 具体可表达为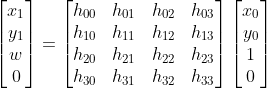 
，
观察可知，删除变换矩阵最后一行与最后一列不影响计算结果，因此，可简化表达式为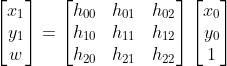 
，
以上变换有 8 个自由度，将变换矩阵重新改写为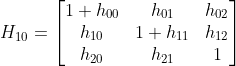 
，
变换矩阵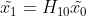 
表达了平面场景的映射关系，这正好是 “图像配准” 一文中使用的模型之一。
3 旋转全景模型
在一个固定的世界坐标下，假设相机绕某旋转点旋转拍照，两次（或多次）拍照间相机坐标原点保持不变，但光轴随旋转发生改变。
三维空间中任意固定点在每次拍照中的映射可表达为：
1）建立相机坐标系（原点与世界坐标系一致，光轴为相机当前光轴）；
2）使用旋转矩阵 R 将世界坐标系下点旋转为相机坐标系下点；
3）使用投影矩阵投影到相机平面；
因此，三维空间点在两幅图像中的映射关系可简化为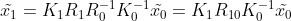 
，
假设 K 仅包含相机焦距信息，则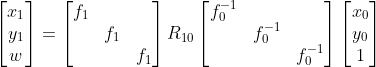 
，
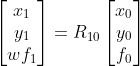，当焦距已知时，此参数仅为旋转，当焦距未知时，可以是固定焦距或者变化焦距。
一般情况下，该变化的参数个数为 4，包括 1）固定未知焦距，2）旋转参数（3个），
这比8个参数投影变换更加简化，该模型是用于全景图像拼接的理想模型。
4 迭代求解
给定一对图像上若干匹配点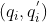 
，使用平面投影变换可得 
，
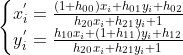两边同时乘以分母得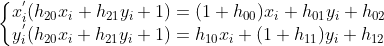 
，
进一步整理为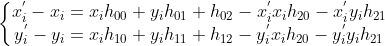 
，
使用该线性方程组可以求解变换矩阵 
的初始估计。
在初始估计 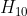基础上使用非线性迭代方程为 
,
，
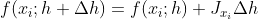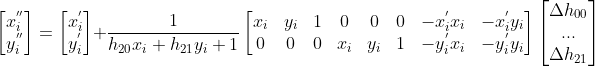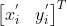为变换矩阵 的估计，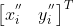
为第二次迭代估计，通过最小化第二次估计误差即求得合理的 
。
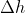如果在每次迭代估计中使用上次迭代估计值 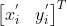作为初始估计，即 中各个参数值均为零，迭代方程可改写为
，
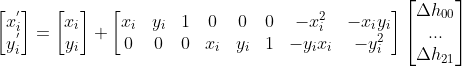注意，以上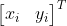 
不再是初始匹配点，而是每次迭代后的计算点！！！
在旋转全景模型中，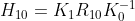
，当旋转分量增加 
后，
旋转矩阵为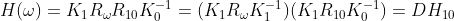 
, 
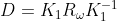为增量矩阵。
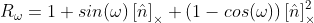，当 为弧度单位且很小时，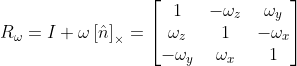
，
，
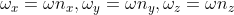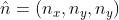表示旋转轴。
增量矩阵 D 可改写为 
，
D 中变量为旋转角度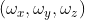 
，使用线性近似可表达为 
，
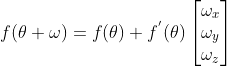其中，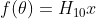
为初始估计参数的变换结果，
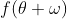为旋转一个小的角度 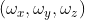后的线性变换结果，
使用最小二乘法可以求解一个合理的旋转角度。
观察增量矩阵 D，可以发现 D 与 H 存在一种对应关系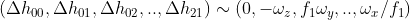 
，
迭代公式 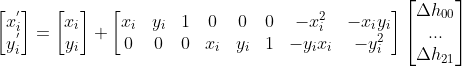可转换为：
，
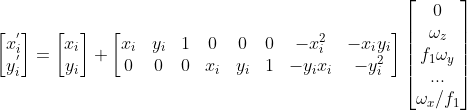整理公式，使其为 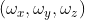的线性函数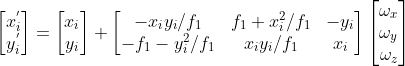 
，
使用最小二乘法可以求解一个合理的旋转角度。
未完......
参考资料 Computer Vision: Algorithms and Applications Richard Szeliski
原文：https://www.cnblogs.com/luofeiju/p/14291846.html