线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
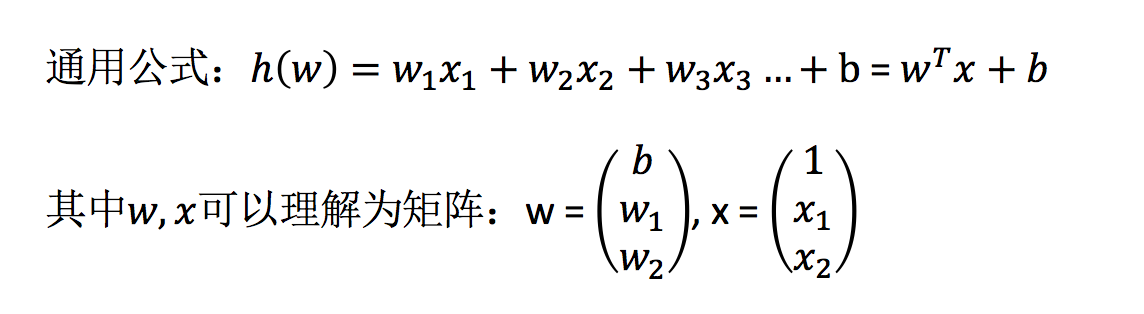
线性回归当中的关系有两种,一种是线性关系,另一种是非线性关系。线性关系一定是线性模型。线性模型不一定是线性关系
总损失定义为:
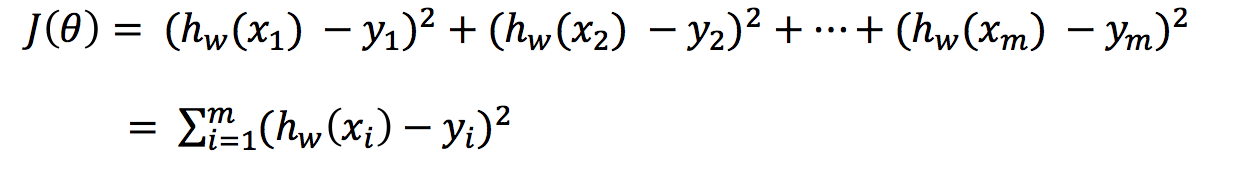
如何去求模型当中的W,使得损失最小?(目的是找到最小损失对应的W值)
线性回归经常使用的两种优化算法
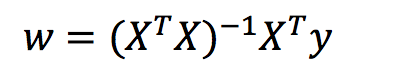
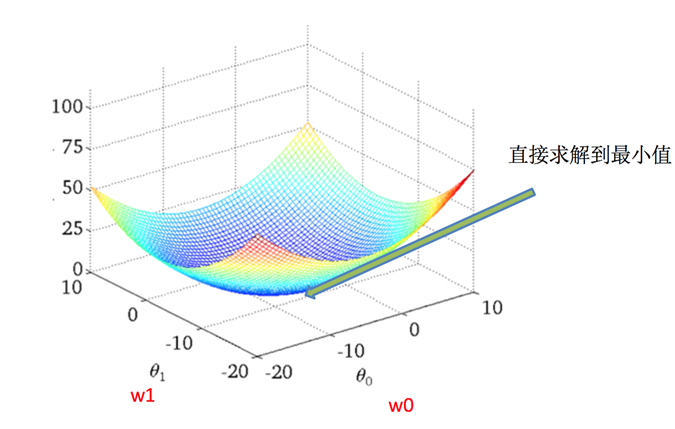
解释: X为特征值矩阵,y为目标值矩阵。
缺点:当特征过多过复杂时,求解速度太慢并且得不到结果
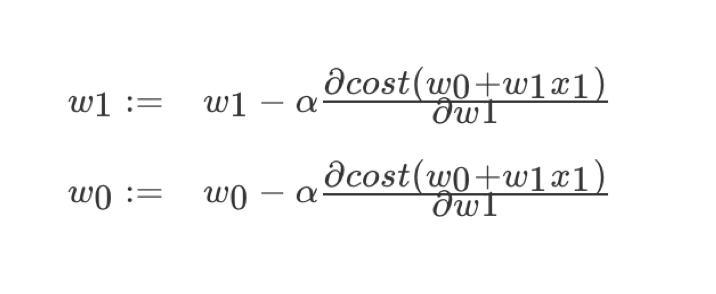
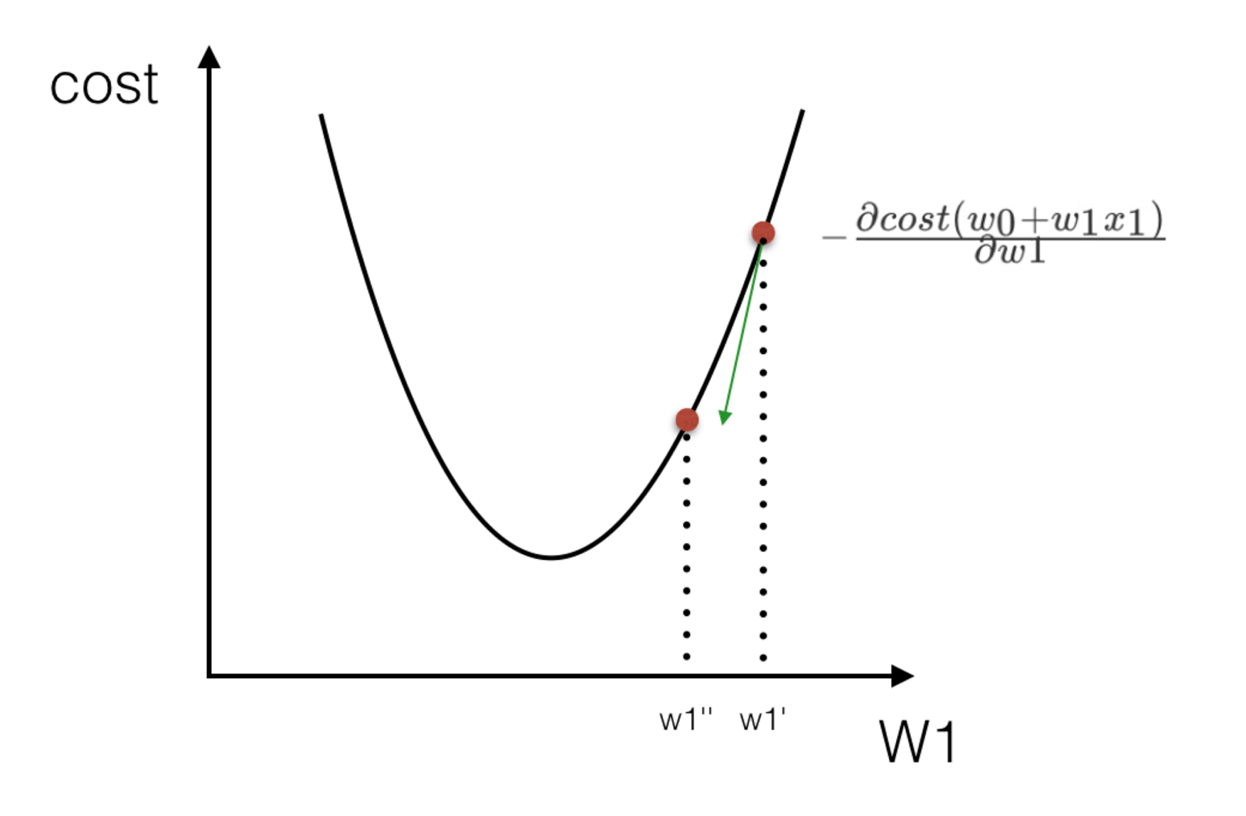
解释:α为学习速率,需要手动指定(超参数),α旁边的整体表示方向
使用:面对训练数据规模十分庞大的任务 ,能够找到较好的结果
均方误差(Mean Squared Error)MSE)评价机制:
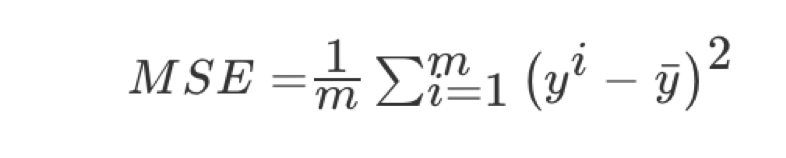
注:y^i为预测值,ˉy为真实值
sklearn.metrics.mean_squared_error(y_true, y_pred)
def linear1(): """ 正规方程的优化方法对波士顿房价进行预测 :return: """ # 1)获取数据 boston = load_boston() # 2)划分数据集 x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22) # 3)标准化 transfer = StandardScaler() x_train = transfer.fit_transform(x_train) x_test = transfer.transform(x_test) # 4)预估器 estimator = LinearRegression() estimator.fit(x_train, y_train) # 5)得出模型 print("正规方程-权重系数为:\n", estimator.coef_) print("正规方程-偏置为:\n", estimator.intercept_) # 6)模型评估 y_predict = estimator.predict(x_test) print("预测房价:\n", y_predict) error = mean_squared_error(y_test, y_predict) print("正规方程-均方误差为:\n", error) return None
def linear2(): """ 梯度下降的优化方法对波士顿房价进行预测 :return: """ # 1)获取数据 boston = load_boston() print("特征数量:\n", boston.data.shape) # 2)划分数据集 x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22) # 3)标准化 transfer = StandardScaler() x_train = transfer.fit_transform(x_train) x_test = transfer.transform(x_test) # 4)预估器 estimator = SGDRegressor(learning_rate="constant", eta0=0.01, max_iter=10000, penalty="l1") estimator.fit(x_train, y_train) # 5)得出模型 print("梯度下降-权重系数为:\n", estimator.coef_) print("梯度下降-偏置为:\n", estimator.intercept_) # 6)模型评估 y_predict = estimator.predict(x_test) print("预测房价:\n", y_predict) error = mean_squared_error(y_test, y_predict) print("梯度下降-均方误差为:\n", error) return None
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 | 不需要 |
| 需要迭代求解 | 一次运算得出 |
| 特征数量较大可以使用 | 需要计算方程,时间复杂度高O(n3) |
原文:https://www.cnblogs.com/MoooJL/p/14318941.html