keras是基于python的高级神经网路API.keras必须有后端才可以运行,后端可以切换。它以特别方便快速试验,帮助用户以最少的时间验证自己的想法,帮助用户以最少的时间验证自己的想法。
Tf-keras和keras联系
它们都基于同一套API,keras程序可以通过改导入方式轻松转为tf.keras程序
反之不能成立,因为tf.keras有其他特性,而keras不能满足
它们有相同的JOSN和HDF5模型序列化格式和语义
tf-keras和keras区别
1.tf.keras全面支持动态图模式
2.只用keras.Sequential和keras.Model时没影响。自定义Model内部运算逻辑的时候有影响
3.TF.keras支持基于tf.data模型训练,支持TPU训练,支持tf.distribution中分布式策略。Tf.keras可以与tensorflow中estimator集成,tf.keras可以保存SavedModel
分类问题其实是预测当前所属类别,通过模型输出的是它的概率分布,而回归问题预测的是值,模型输出的是一个实际值。
回归问题,预测预测值与真实值之间差距。
目标函数
为什么需要目标函数?
这是机器学习特性所决定的,大部分机器学习都是逐步调整参数得到最优解,从而逼近目标值。而目标函数可以帮助衡量模型好坏程度。
比如一个分类问题:它能衡量目标类别与当前预测的差距。通过One-hot编码,把一个正整数变为向量表达(生成一个长度不小于正整数向量,只有正整数的位置处于1,其余处于0)。
分类问题常用方式:
平方差损失
平方差损失距离:
预测值: [0.2, 0.7, 0.1]
真实值: [0, 0, 1]
损失函数值: [(0-0)^2 + (0.7-0)^2 + (0.1-1)^2]*0.5 = 0.65
交叉熵损失
我们采用tensorflow内置图片数据集进行示例:fashion_mnist
# tf.keras 分类模型
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import sklearn
import pandas as pd
import os
import sys
import time
import tensorflow as tf
from tensorflow import keras
# 打印版本
print(tf.__version__)
print(sys.version_info)
for module in mpl,np,pd,sklearn,tf,keras:
print(module.__name__, module.__version__)
"""
2.1.0
sys.version_info(major=3, minor=7, micro=5, releaselevel=‘final‘, serial=0)
matplotlib 3.3.3
numpy 1.19.5
pandas 1.2.1
sklearn 0.24.0
tensorflow 2.1.0
tensorflow_core.keras 2.2.4-tf
"""
# 导入内置图片数据集
fashion_mnist = keras.datasets.fashion_mnist
# 训练集 测试集
(x_train_all,y_train_all),(x_test,y_test) = fashion_mnist.load_data()
# 拆分前5000张作为验证集,剩下作为训练集
x_valid, x_train = x_train_all[:5000], x_train_all[5000:]
y_valid, y_train = y_train_all[:5000], y_train_all[5000:]
# 打印大小
print(x_valid.shape, y_valid.shape)
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
"""
(5000, 28, 28) (5000,)
(55000, 28, 28) (55000,)
(10000, 28, 28) (10000,)
"""
def show_single_image(img_arr):
"""
展示查看一张图片
"""
plt.imshow(img_arr,cmap="binary")
show_single_image(x_train[0])
def show_imgs(n_rows, n_cols,x_data,y_data,class_names):
"""
展示图片集
class_names 索引
"""
#
assert len(x_data) == len(y_data)
# 验证行和列的乘积不能大于样本数
assert n_rows * n_cols < len(x_data)
# 定义图大小
plt.figure(figsize=(n_cols * 1.4, n_rows * 1.6))
# 对每行每列放图片
for row in range(n_rows):
for col in range(n_cols):
index = n_cols * row + col
# 绘制子图
plt.subplot(n_rows, n_cols, index+1)
# 展示数据 interpolation缩放图片
plt.imshow(x_data[index], cmap="binary",interpolation="nearest")
# 关闭坐标系
plt.axis("off")
# 配置title
plt.title(class_names[y_data[index]])
plt.show()
class_names = ["T-shirt","Trouser","Pullover","Dress","Coat","Sandal","Shirt","Sneaker","Bag", "Ankle boot"]
# 显示3行5列
show_imgs(3, 5,x_train,y_train,class_names)

# 使用tf.keras.models.Sequential 进行分类
# 写法1:
# Sequential对象
model = keras.models.Sequential()
# 往对象添加层次:
# 添加输入层,并将其展开 : 我输入的是28*28矩阵,用Flatten进行展平,成为一个一维向量
model.add(keras.layers.Flatten(input_shape=[28,28]))
# 添加全连接层 单元数:300(它是用层次发掘神经网络,上一层神经单元和下一层神经单元一一进行连接) activation表示激活函数
model.add(keras.layers.Dense(300, activation="relu"))
# 再添加全连接层 单元数:100
model.add(keras.layers.Dense(100, activation="relu"))
model.add(keras.layers.Dense(10, activation="softmax"))
# relu: y = max(0,x)
# softmax: 将向量变成概率分布输出
# x=[x1,x2,x3]
# y = [e^x1/sum , e^x2/sum, e^x3/sum], sum = e^x1 + e^x2 + e^x3
# 写法2:
# model = keras.models.Sequential([
# keras.layers.Flatten(input_shape=[28,28]),
# keras.layers.Dense(300, activation="relu"),
# keras.layers.Dense(100, activation="relu"),
# keras.layers.Dense(10, activation="softmax")
# ])
# 因为y是一个index值,我们需要将y 经过one_hot 变成一个向量
# 如果y是一个向量用categorical_crossentropy即可
# optimizer 为求解优化器方法: 这里使用adam
# metrics : 把损失函数,优化方法加入 keras.optimizers.SGD(lr = 0.1)
model.compile(loss="sparse_categorical_crossentropy",optimizer="adam", metrics=["accuracy"])
# 查看模型层数
model.layers
"""
[<tensorflow.python.keras.layers.core.Flatten at 0x7fa359641750>,
<tensorflow.python.keras.layers.core.Dense at 0x7fa359641950>,
<tensorflow.python.keras.layers.core.Dense at 0x7fa359645490>,
<tensorflow.python.keras.layers.core.Dense at 0x7fa359645050>]
"""
# 查看模型概况
model.summary()
"""
Model: "sequential_7"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_7 (Flatten) (None, 784) 0
_________________________________________________________________
dense_21 (Dense) (None, 300) 235500
_________________________________________________________________
dense_22 (Dense) (None, 100) 30100
_________________________________________________________________
dense_23 (Dense) (None, 10) 1010
=================================================================
Total params: 266,610
Trainable params: 266,610
Non-trainable params: 0
_________________________________________________________________
"""
# 整个层数解析:
# 第一层:是样本数 乘以 784 矩阵
# 第二层:进入全连接层 将其变成样本数 * 300 矩阵 (变换过程: 【样本数 乘以 784 】 * W(权重, W为[784,300]矩阵) + b(偏执, b为300长的向量))
# 第三层,第四层也是如上方式实现
# 训练模型
# epochs:将训练集运行10次
# validation_data:对训练集进行验证
history = model.fit(x_train,y_train, epochs=10,validation_data=(x_valid,y_valid))
"""
Train on 55000 samples, validate on 5000 samples
Epoch 1/10
55000/55000 [==============================] - 5s 95us/sample - loss: 2.0006 - accuracy: 0.7321 - val_loss: 0.6174 - val_accuracy: 0.8032
Epoch 2/10
55000/55000 [==============================] - 4s 81us/sample - loss: 0.5339 - accuracy: 0.8135 - val_loss: 0.4758 - val_accuracy: 0.8424
Epoch 3/10
55000/55000 [==============================] - 5s 99us/sample - loss: 0.4774 - accuracy: 0.8339 - val_loss: 0.4359 - val_accuracy: 0.8538
Epoch 4/10
55000/55000 [==============================] - 5s 91us/sample - loss: 0.4468 - accuracy: 0.8447 - val_loss: 0.4878 - val_accuracy: 0.8392
Epoch 5/10
55000/55000 [==============================] - 5s 95us/sample - loss: 0.4269 - accuracy: 0.8511 - val_loss: 0.4067 - val_accuracy: 0.8642
Epoch 6/10
55000/55000 [==============================] - 5s 93us/sample - loss: 0.4076 - accuracy: 0.8551 - val_loss: 0.3962 - val_accuracy: 0.8728
Epoch 7/10
55000/55000 [==============================] - 5s 97us/sample - loss: 0.4024 - accuracy: 0.8594 - val_loss: 0.3951 - val_accuracy: 0.8690
Epoch 8/10
55000/55000 [==============================] - 5s 98us/sample - loss: 0.3881 - accuracy: 0.8627 - val_loss: 0.4112 - val_accuracy: 0.8626
Epoch 9/10
55000/55000 [==============================] - 5s 95us/sample - loss: 0.3734 - accuracy: 0.8691 - val_loss: 0.4331 - val_accuracy: 0.8550
Epoch 10/10
55000/55000 [==============================] - 5s 95us/sample - loss: 0.3594 - accuracy: 0.8727 - val_loss: 0.3709 - val_accuracy: 0.8800
history.history
"""
def plot_learning_curves(history):
"""
查看训练结果图
"""
# 设置图像大小
pd.DataFrame(history.history).plot(figsize=(8,5))
# 显示网格
plt.grid(True)
# 坐标轴范围
plt.gca().set_ylim(0,1)
plt.show()
plot_learning_curves(history)
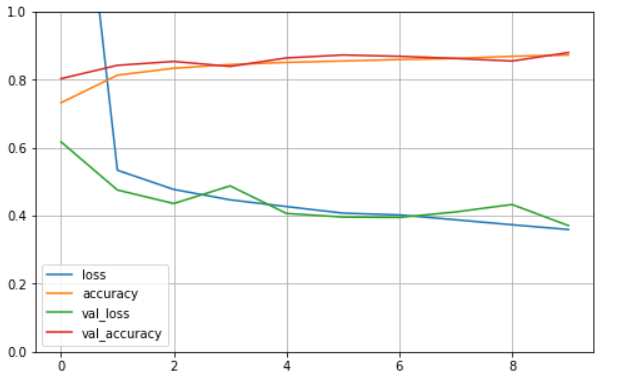
# 这里使用sklearn进行归一化
# 导入内置图片数据集
fashion_mnist = keras.datasets.fashion_mnist
# 训练集 测试集
(x_train_all,y_train_all),(x_test,y_test) = fashion_mnist.load_data()
# 拆分前5000张作为验证集,剩下作为训练集
x_valid, x_train = x_train_all[:5000], x_train_all[5000:]
y_valid, y_train = y_train_all[:5000], y_train_all[5000:]
print(x_valid.shape, y_valid.shape)
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
"""
(5000, 28, 28) (5000,)
(55000, 28, 28) (55000,)
(10000, 28, 28) (10000,)
"""
print(np.max(x_train), np.min(x_train))
# 255 0
# 归一化
#
# x = (x - avg) /std
# avg是均值
# std是方差
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
# 训练集做归一化
# 归一化只能进行二维矩阵归一化,因为x_train是三维矩阵,首先将它转为二维矩阵,然后归一化,然后再转回三维矩阵
x_train_scaled = scaler.fit_transform(x_train.astype(np.float32).reshape(-1,1)).reshape(-1,28,28)
# 验证集做归一化
x_valid_scaled = scaler.transform(x_valid.astype(np.float32).reshape(-1,1)).reshape(-1,28,28)
# 测试集做归一化
x_test_scaled = scaler.transform(x_test.astype(np.float32).reshape(-1,1)).reshape(-1,28,28)
print(np.max(x_train_scaled), np.min(x_train_scaled))
# 2.0231433 -0.8105136
history = model.fit(x_train_scaled,y_train, epochs=10,validation_data=(x_valid_scaled,y_valid))
"""
Train on 55000 samples, validate on 5000 samples
Epoch 1/10
55000/55000 [==============================] - 5s 95us/sample - loss: 0.4586 - accuracy: 0.8323 - val_loss: 0.3790 - val_accuracy: 0.8560
Epoch 2/10
55000/55000 [==============================] - 6s 104us/sample - loss: 0.3526 - accuracy: 0.8701 - val_loss: 0.3577 - val_accuracy: 0.8718
Epoch 3/10
55000/55000 [==============================] - 5s 95us/sample - loss: 0.3154 - accuracy: 0.8826 - val_loss: 0.3366 - val_accuracy: 0.8758
Epoch 4/10
55000/55000 [==============================] - 5s 93us/sample - loss: 0.2916 - accuracy: 0.8909 - val_loss: 0.3162 - val_accuracy: 0.8854
Epoch 5/10
55000/55000 [==============================] - 5s 91us/sample - loss: 0.2722 - accuracy: 0.8972 - val_loss: 0.3546 - val_accuracy: 0.8720
Epoch 6/10
55000/55000 [==============================] - 5s 92us/sample - loss: 0.2593 - accuracy: 0.9024 - val_loss: 0.3358 - val_accuracy: 0.8800
Epoch 7/10
55000/55000 [==============================] - 5s 90us/sample - loss: 0.2395 - accuracy: 0.9095 - val_loss: 0.3286 - val_accuracy: 0.8894
Epoch 8/10
55000/55000 [==============================] - 5s 91us/sample - loss: 0.2318 - accuracy: 0.9122 - val_loss: 0.3225 - val_accuracy: 0.8900
Epoch 9/10
55000/55000 [==============================] - 5s 88us/sample - loss: 0.2172 - accuracy: 0.9185 - val_loss: 0.3302 - val_accuracy: 0.8930
Epoch 10/10
55000/55000 [==============================] - 5s 89us/sample - loss: 0.2101 - accuracy: 0.9202 - val_loss: 0.3380 - val_accuracy: 0.8942
"""
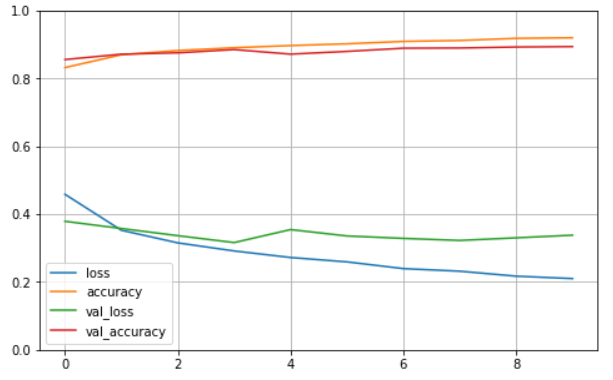
由上面可以知道归一化的训练后结果准确率:达到最高92%
验证准确率
model.evaluate(x_test_scaled, y_test)
"""
10000/10000 [==============================] - 0s 37us/sample - loss: 0.3633 - accuracy: 0.8853
[0.3633375147640705, 0.8853]
"""
loss 0.3633375147640705
准确度:0.8853
当你在训练模型时候,你中间可以做一些事情,常用回调函数:
EarlyStopping 当模型训练时候当你的loss在不断下降时候,我们可以提前停掉
ModelCheckpoint 将在每个epoch后保存模型到filepath
TensorBoard 模型训练过程中可以显示训练结果状态
只需在model.fit调用回调函数
# Tensorboard
logdir = "./callbacks"
# 创建目录
if not os.path.exists(logdir):
os.mkdir(logdir)
# 定义输出文件
output_model_file = os.path.join(logdir, "fashion_mnist_model.h5")
callbacks = [
keras.callbacks.TensorBoard(logdir),
# save_best_only保存最好模型
keras.callbacks.ModelCheckpoint(output_model_file, save_best_only=True),
# patience 当下一次训练比上一次训练小的时候,连续发生多少次,就要停掉
# min_delta 阈值, 当前次训练比上一次训练要低于这个值会停掉
keras.callbacks.EarlyStopping( patience=5,min_delta=1e-3)
]
history = model.fit(x_train_scaled,y_train, epochs=10,validation_data=(x_valid_scaled,y_valid),callbacks=callbacks)
命令行中callbacks目录下执行tensorboard --logdir=callbacks --host=0.0.0.0获取详细信息
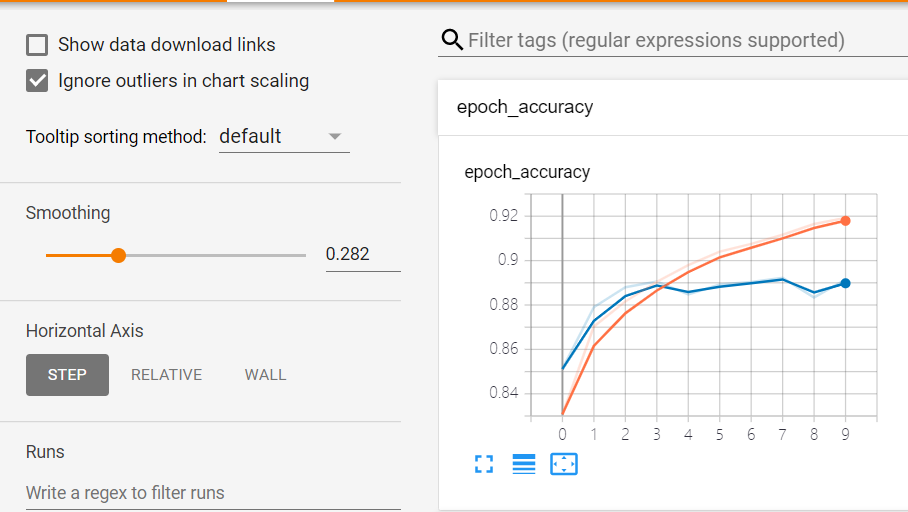
??
在我们构建模型层次时候,使用激活函数,激活函数有如下
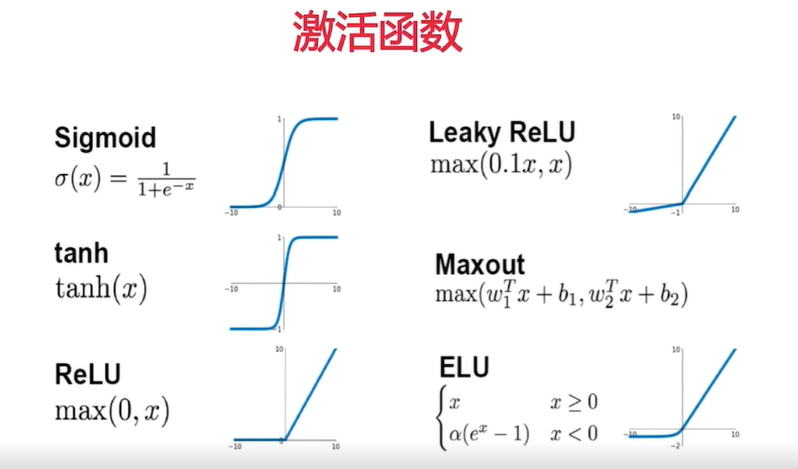
它们将非线性特性引入到我们的网络中。其主要目的是将模型中一个节点的输入信号转换成一个输出信号。该输出信号现在被用作堆叠中下一个层的输入。
其实它就是将输入输出数据进行规整,使它的均值为0,方差为1。常用归一化种类
Min-max归一化: x*=(x-min)/(max-min)
Z-score归一化: x*=(x-μ)/σ
批归一化
将每层激活值都做归一化
为什么归一化有效,如下图:
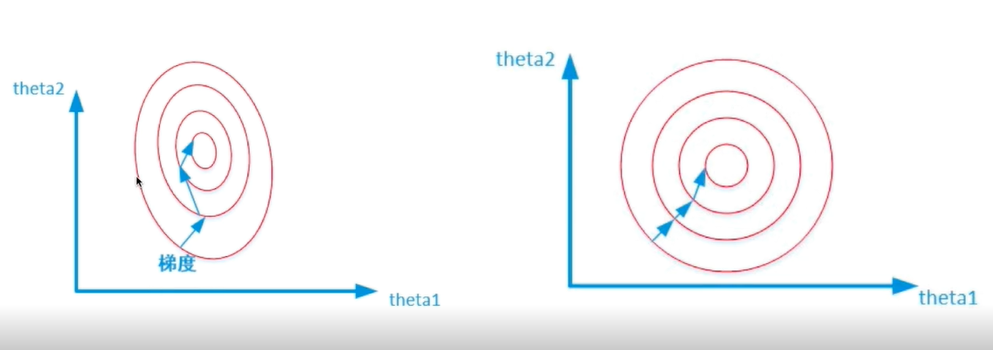
图一没有做归一化处理导致theta1与theta2值是不一样的。这样由于theta1与theta2值是不一样,等高线看起来像是一个椭圆,(等高线解释:等高线表示在这条等高线的值都是一样的),但是目标函数值是一样的。因为它是椭圆,在计算法向量时候没有指向圆心,导致训练轨迹非常曲折。
经过归一化如图二,当然训练速度也会更快
Dropout是一种在深度学习环境中应用的正规化手段。它是这样运作的:在一次循环中我们先随机选择神经层中的一些单元并将其临时隐藏,然后再进行该次循环中神经网络的训练和优化过程。在下一次循环中,我们又将隐藏另外一些神经元,如此直至训练结束。Dropout
Droupout作用
作用可以防止过拟合:
(什么是过拟合:训练集上表现很好,测试集上不好)---造成这样原因可能模型参数比较多,容量太大,使得模型记住样本(测试集的样本和训练集样本是不一样),不能泛华
还是以上面为例只不过我们添加学习网络时,增加20层
# 使用tf.keras.models.Sequential 进行分类
# Sequential对象
model = keras.models.Sequential()
# 往对象添加层次:
# 添加输入层,并将其展开 : 我输入的是28*28矩阵,用Flatten进行展平,成为一个一维向量
model.add(keras.layers.Flatten(input_shape=[28,28]))
# 添加20层学习网络
for _ in range(20):
model.add(keras.layers.Dense(100, activation="relu"))
model.add(keras.layers.Dense(10,activation="softmax"))
此时打印训练结果图
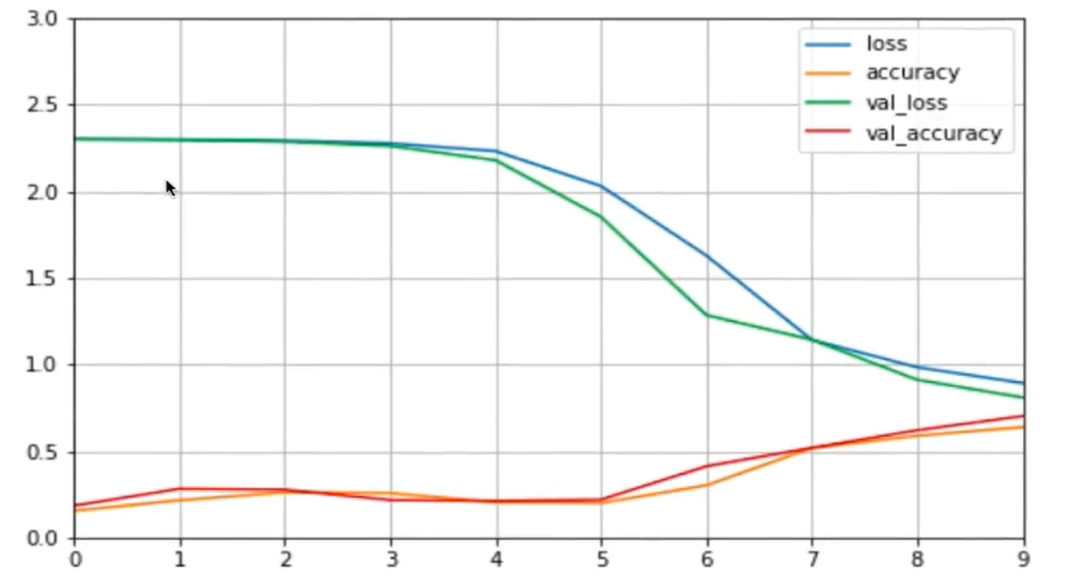
由上图我们发现,相对于之前学习曲线图在初期时候(x轴0到3之间),目标函数趋势是不怎么发生变化的。而把目标函数迭代到x轴为4时,目标函数才变化的陡峭,导致原因是:
1. 由于是深度学习,参数比较多,训练不充分。
2. 梯度消失:一般发生在深度学习网络里,导致发生原因为链式法则,(链式法则用于复合函数求导f(g(x)), 函数g(x)输出是f函数输入)。对于低层次神经网络,它的复合函数嵌套较多,梯度一层一层传导下去,到低层次因符合函数嵌套较多,就有可能导致梯度消失,导致训练结果比较平滑,梯度消失
批归一化实现
model.add(keras.layers.BatchNormalization())
model.add(keras.layers.Dense(100))# 添加学习层次
model.add(keras.layers.BatchNormalization())# 批归一化
model.add(keras.layers.Activation(‘relu‘))# 添加激活后面
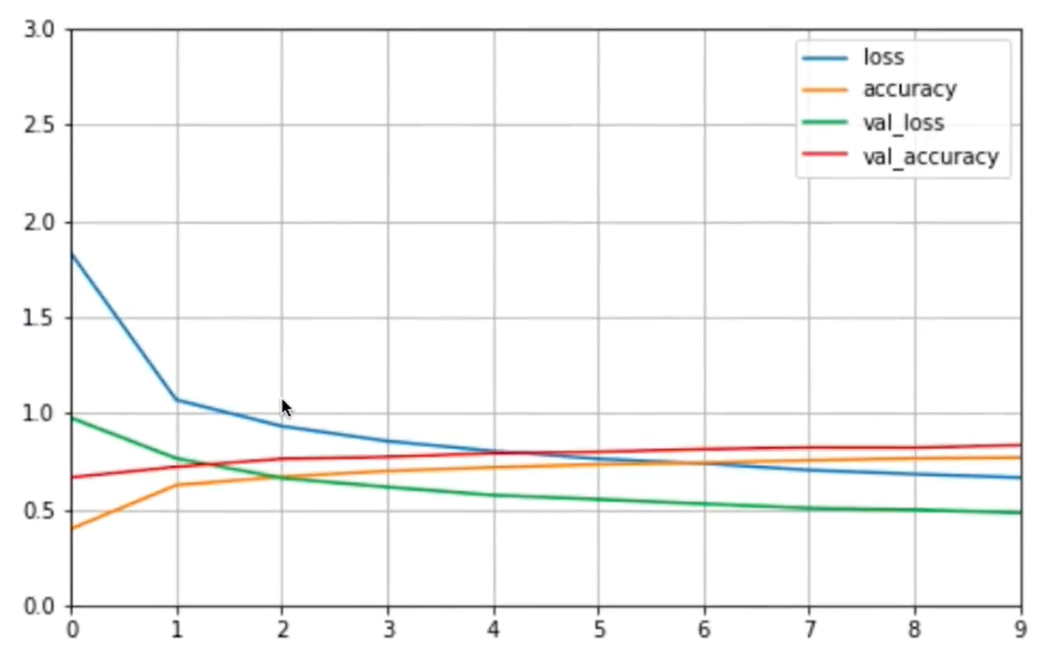
我们可以看到进行批归一化训练的模型,没有了上述问题。我们通过批归一化缓解梯度消失,通过归一化是数据更加规整,这样计算更加准确
激活函数更改带来效果
model.add(keras.layers.Dense(100, activation="selu"))
dropout添加
# rate为添加单元比例
# 添加AlphaDropout
model.add(keras.layers.AlphaDropout(rate=0.5))
# 添加普通Dropout方式
model.add(keras.layers.Dropout(rate=0.5))
AlphaDropout 比 Dropout更加强大,AlphaDropout优势:均值和方差不变,归一化的性质也不变。
Dropout使用,根据自己训练场景定,如果没有出现过拟合现象可以不用使用Dropout
用于分类和回归的模型,并应用到了 Google Play 的应用推荐中。wide and deep 模型的核心思想是结合线性模型的记忆能力(memorization)和 DNN 模型的泛化能力(generalization),在训练过程中同时优化 2 个模型的参数,从而达到整体模型的预测能力最优。
稀疏特征:
什么是稀疏特征:
比如我们100维度的向量(x1,x2,....x100),我们通过x1,x2,x3来表示即可,其他参数约束为0,那么他就是一种稀疏表示思想。
它是一个离散值特征,使用One-hot表示。而稀疏特征可以进行叉乘,叉乘可以有效刻画样本,通过稀疏特征做叉乘取出共现信息,实现模型记忆效果。
有一个词表: [你,他, 计算机] 经过one-hot ===> 他=[0,0,1,...] 计算机=[1,0,1,...]
进行叉乘 : (他,计算机)
优缺点:
优点:
降低表示复杂度,更直白的原因其实就是减少系数参数,通过稀疏表示,可以充分发挥数据所含有的信息,去掉冗余的数据信息,达到最大化利用数据,广泛用于工业界
缺点:
需要人工设计
可能过拟合,所有特征都叉乘,相当于记住每一个样本
密集特征
用向量表达特征
有一个词表: [你,他, 计算机] 经过one-hot ===> 他=[0,0,1,...] 计算机=[1,0,1,...]
他 用一个向量来表示 [0.2,0.5,0.3,...(n维向量)]
Word2vec工具就是词语转化成向量。
优缺点
优点:
带有语义信息,不同向量之间有相关性
兼容没有出现过的特征组合
更少的人工去设计
缺点:
过度泛化,导致推荐不怎么相关的产品
wide 和deep模型结构
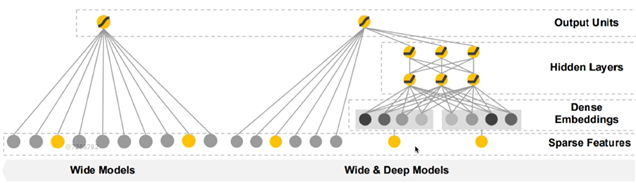
图像左侧为wide模型
右侧为wide&deep模型
wide模型
它所有输入都连接输出上,输入就是系数特征(one-hot表达)
wide&deep
左半部分是一个wide模型
右半部分是deep模型,他是多层的模型。首先输入是稀疏特征,deep把说有输入数据作为一个密集的向量表达,然后进行多层的全连接网络,最后连接到输出。
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import sklearn
import pandas as pd
import os
import sys
import time
import tensorflow as tf
from tensorflow import keras
# 打印版本
print(tf.__version__)
print(sys.version_info)
for module in mpl,np,pd,sklearn,tf,keras:
print(module.__name__, module.__version__)
# 导入fetch_california_housing类
from sklearn.datasets import fetch_california_housing
# 实例化对象
housing = fetch_california_housing()
# 打印相关信息
print(housing.DESCR)
print(housing.data.shape)
# 输出:(20640, 8)
print(housing.target.shape)
# 输出:(20640,)
from sklearn.model_selection import train_test_split
#拆分训练集,测试集
x_train_all,x_test,y_train_all,y_test = train_test_split(
housing.data , housing.target , random_state=7,test_size = 0.2)
# 拆分训练集,验证集
x_train,x_valid,y_train,y_valid = train_test_split(
x_train_all , y_train_all , random_state=11)
"""
train_test_split类里面传入housing.data-(20640, 8),
housing.targget-(20640,)
随机种子-random.state
(train_test_split 默认划分比例是3:1
也可以通过test_size,改变比例,
默认test_size = 0.25)
"""
print(x_train.shape,y_train.shape)
print(x_valid.shape,y_valid.shape)
print(x_test.shape,y_test.shape)
#导入StandardScaler类
from sklearn.preprocessing import StandardScaler
# 实例化
scaler = StandardScaler()
# 调用scaler。fit 或者scaler.transform方法
x_train_scaled = scaler.fit_transform(x_train)
x_valid_scaled = scaler.transform(x_valid)
x_test_scaled = scaler.transform(x_test)
# 使用函数式API功能实现
# 定义输入层 将数据读取
input = keras.layers.Input(shape=x_train.shape[1:])
# 使用2层神经网络实现deep model 有点类似复合函数 fx(x) = h(g(x))
hidden1 = keras.layers.Dense(30, activation=‘relu‘)(input)# 第一层
hidden2 = keras.layers.Dense(30, activation=‘relu‘)(hidden1)# 第二层
# wide输入和神经网络层输出合并
concat = keras.layers.concatenate([input, hidden2])
# 最后输出
output = keras.layers.Dense(1)(concat)
# 定义model 函数式需要定义model
model = keras.models.Model(inputs=[input],outputs=[output])
model.compile(loss="mean_squared_error",optimizer="adam", metrics=["accuracy"])
callbacks = [
keras.callbacks.EarlyStopping( patience=5,min_delta=1e-3)
]
history = model.fit(x_train_scaled,y_train, epochs=100,validation_data=(x_valid_scaled,y_valid), callbacks=callbacks)
def plot_learning_curves(history):
"""
查看训练结果图
"""
# 设置图像大小
pd.DataFrame(history.history).plot(figsize=(8,5))
# 显示网格
plt.grid(True)
# 坐标轴范围
plt.gca().set_ylim(0,1)
plt.show()
plot_learning_curves(history)
# 子类API
class WideDeepModel(keras.models.Model):
def __init__(self):
super(WideDeepModel, self).__init__()
# 定义模型层次
self.hidden1_layer = keras.layers.Dense(30, activation="relu")# 全连接层1
self.hidden2_layer = keras.layers.Dense(30, activation="relu")# 全连接层2
self.output_layer = keras.layers.Dense(1)# 输出层 ,长度为1
def call(self, input):
"""完成模型正向计算"""
hideen1 = self.hidden1_layer(input)
hideen2 = self.hidden2_layer(hideen1)
concat = keras.layers.concatenate([input, hideen2])
output = self.output_layer(concat)
return output
# 构建model
# 方式1:
# model = WideDeepModel()
# 方式2:
model = keras.models.Sequential([
WideDeepModel(),
])
model.build(input_shape=(None, 8))
model.compile(loss="mean_squared_error",optimizer="adam")
# 多输入
# 函数式实现方法
input_wide = keras.layers.Input(shape=[5])# wide输入:选前5个当wide模型输入
input_deep = keras.layers.Input(shape=[6])# deep输入:选后6个 当deep模型输入
hidden1 = keras.layers.Dense(30, activation=‘relu‘)(input_deep)
hidden2 = keras.layers.Dense(30, activation=‘relu‘)(input_wide)
concat = keras.layers.concatenate([input_wide, hidden2])
# 输出
output = keras.layers.Dense(1)(concat)
# 实例模型
model = keras.models.Model(inputs=[input_wide,input_deep],outputs=[output])
model.compile(loss="mean_squared_error",optimizer="adam")
callbacks = [
keras.callbacks.EarlyStopping( patience=5,min_delta=1e-3)
]
# 训练数据拆分
# wide训练数据取前5个
x_train_scaled_wide = x_train_scaled[:,:5]
# deep训练数据取后5个
x_train_scaled_deep = x_train_scaled[:,2:]
# 测试数据拆分
x_test_scaled_deep = x_test_scaled[:,2:]
x_test_scaled_wide = x_test_scaled[:,:5]
# 验证数据拆分
x_valid_scaled_deep = x_valid_scaled[:,2:]
x_valid_scaled_wide = x_valid_scaled[:,:5]
history = model.fit([x_train_scaled_wide, x_train_scaled_deep],y_train, epochs=100,validation_data=([x_valid_scaled_wide, x_valid_scaled_deep],y_valid), callbacks=callbacks)
# 上例中再定义个输出
# 输出hidden2
output2 = keras.layers.Dense(1)(hidden2)
# 实例模型加入输出
model = keras.models.Model(inputs=[input_wide,input_deep],outputs=[output, output2])
# 训练模型: y_train,y_valid 添加输出训练数据和验证数据
history = model.fit([x_train_scaled_wide, x_train_scaled_deep],[y_train, y_train], epochs=100,validation_data=([x_valid_scaled_wide, x_valid_scaled_deep],[y_valid,y_valid]), callbacks=callbacks)
# 验证增加 y_test验证数据集
model.evaluate([x_test_scaled_wide,x_test_scaled_deep], [y_test,y_test])
网络结构参数:有几层,每层宽度,每层激活函数
训练参数:batch_size,学习率,学习率衰减算法等
而这些参数是不变的,如果手工去实验耗费人力。
搜索策略:
网格搜索
把各种传参数离散化成几个值,吧这几个值一一组合起来,然后一个个去试。
随机搜索
相比网格搜索,网格搜索是将传参数离散化几个固定值,比如值为[0.2,0.4,0.6,0.8] 而最优解是一个0.2-0.4之间的值,这样无法得到最优解。随机搜索是随机的生成参数组合,就能确保最优解是有可能被搜索到的,但随机的组合会比网格搜索更多
遗传算法搜索
遗传算法是对自然界的模拟
1.首先初始化候选参数集合 -> 训练-> 得到模型指标作为生存概率
2.然后根据生存的概率做随机选择 -> 交叉(类似于DNA组合) -> 变异(参数进行微小调整) -> 产生下一代集合
3.重新回到1.
启发式搜索
使用循环神经网络来生成参数,使用强化学习来进行反馈,使用模型来训练生成参数。
# 定义 learning_rate
# W = W + grad + learning_rate
learning_rates = [1e-4,3e-4,1e-3,3e-3,1e-2,3e-2]
histories = []
for lr in learning_rates:
# 实例化训练模型
model = keras.models.Sequential([
keras.layers.Dense(30, activation="relu",input_shape=x_train.shape[1:]),
keras.layers.Dense(1),
])
# 定义优化器
optimizer = keras.optimizers.SGD(lr)
model.compile(loss="mean_squared_error",optimizer=optimizer)# sgd adam
callbacks = [
keras.callbacks.EarlyStopping( patience=5,min_delta=1e-3)
]
# 训练模型
history = model.fit(
x_train_scaled, y_train,
validation_data=(x_valid_scaled, y_valid),
epochs = 10,
callbacks = callbacks
)
histories.append(history)
打印训练图
def plot_learning_curves(history):
"""
查看训练结果图
"""
# 设置图像大小
pd.DataFrame(history.history).plot(figsize=(8,5))
# 显示网格
plt.grid(True)
# 坐标轴范围
plt.gca().set_ylim(0,1)
plt.show()
for lr, history in zip(learning_rates, histories):
print("Learning rate:", lr)
plot_learning_curves(history)
上述手动实现超参数搜索存在着以下问题
1.当前我们只有一个参数,只用一层for循环,如果我们参数有20层,那就会有20层for循环
2.使用for循环导致只能等上一个模型训练完毕才能开始下一个模型训练,没有一个并行化处理
使用RandomizedSearchCV实现超参数搜索,整体步骤是首先将tf.model转化为sklearn的model,定义参数集合,实现超参数搜索
常规导报
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import sklearn
import pandas as pd
import os
import sys
import time
import tensorflow as tf
from tensorflow import keras
# 打印版本
print(tf.__version__)
print(sys.version_info)
for module in mpl,np,pd,sklearn,tf,keras:
print(module.__name__, module.__version__)
导入数据集
# 导入fetch_california_housing类
from sklearn.datasets import fetch_california_housing
# 实例化对象
housing = fetch_california_housing()
# 打印相关信息
print(housing.DESCR)
print(housing.data.shape)
# 输出:(20640, 8)
print(housing.target.shape)
拆分训练集,测试集
from sklearn.model_selection import train_test_split
#拆分训练集,测试集
x_train_all,x_test,y_train_all,y_test = train_test_split(
housing.data , housing.target , random_state=7,test_size = 0.2)
# 拆分训练集,验证集
x_train,x_valid,y_train,y_valid = train_test_split(
x_train_all , y_train_all , random_state=11)
print(x_train.shape, y_train.shape)
print(x_valid.shape, y_valid.shape)
print(x_test.shape, y_test.shape)
数据标准化
#导入StandardScaler类
from sklearn.preprocessing import StandardScaler
# 实例化
scaler = StandardScaler()
# 调用scaler。fit 或者scaler.transform方法
x_train_scaled = scaler.fit_transform(x_train)
x_valid_scaled = scaler.transform(x_valid)
x_test_scaled = scaler.transform(x_test)
将tf.model转化为sklearn的model
callbacks = [
keras.callbacks.EarlyStopping( patience=5,min_delta=1e-3)
]
# 将tf.model转化为sklearn的model
def build_model(hidden_layers=1,layer_size=30,learning_rate=3e-3):
"""
hidden_layers中间层的层数
layer_size 默认30
learning_rate 学习率
"""
# 实例化一个训练model
model = keras.models.Sequential()
# 添加全连接层
model.add(keras.layers.Dense(layer_size, activation=‘relu‘, input_shape=x_train.shape[1:]))
# 添加hidden_layers 个全连接层
for _ in range(hidden_layers):
model.add(keras.layers.Dense(layer_size, activation=‘relu‘))
# 添加输出层
model.add(keras.layers.Dense(1))
# 定义优化器
optimizer = keras.optimizers.SGD(learning_rate)
# mse为mean_squared_error简称
model.compile(loss="mse",optimizer=optimizer)# sgd adam
return model
# sklearn_model = keras.wrappers.scikit_learn.KerasRegressor(build_model)
history = sklearn_model.fit(x_train_scaled, y_train, epochs=10, validation_data=(x_valid_scaled,y_valid),callbacks=callbacks)
定义搜索空间
param_distribution = {
"hidden_layers": [1,2,3,4,5],
"layer_size":np.arange(1,100),# 为1-100连续取值
"learning_rate": reciprocal(1e-4,1e-2)# 为一个分布取值
}
scipy 的reciprocal
from scipy.stats import reciprocal
reciprocal.rvs(1e-4,1e-2,size=10)# 生成10的-4次方到10的-2次方 的 10个数
"""
array([0.00407106, 0.00033841, 0.00018518, 0.00246045, 0.00991374,
0.00079176, 0.00011086, 0.00023637, 0.00359715, 0.00372375])
"""
RandomizedSearchCV超参数搜搜
from sklearn.model_selection import RandomizedSearchCV
# 初始化对象
# n_iter 从param_distribution 生成多少个集合
# n_jobs 并行处理数量
# cv 默认为3 使用了cross_validation: 训练集分成n份,n-1训练,最后一份验证
random_search_cv = RandomizedSearchCV(sklearn_model,param_distribution,cv=3, n_iter=10,n_jobs=1)
# 进行训练
random_search_cv.fit(x_train_scaled,y_train,epochs=100,validation_data=(x_valid_scaled,y_valid), callbacks=callbacks)
查看结果
# 查看最好参数
print(random_search_cv.best_params_)
# 查看最好峰值
print(random_search_cv.best_score_)
# 最好model
print(random_search_cv.best_estimator_)
拿取最好model进行验证
# 拿取最好model进行验证
model = random_search_cv.best_estimator_.model
model.evaluate(x_test_scaled, y_test)
原文:https://www.cnblogs.com/xujunkai/p/14322225.html