采用的测试数据:参考上一篇博客4.1部分
https://i.cnblogs.com/posts/edit;postId=14340924
1、实现使用梯度下降求解的逻辑回归算法
import numpy as np #d定义梯度下降法求解的迭代公式 def logistic_regression(X,y,learning_rate,max_iter=1000): #初始化w w=np.zeros(X.shape[1]) for t in range(max_iter): #计算yx yx=y.values.reshape((len(y),1))*X #计算1+e^(yXW) logywx=(1+np.power(np.e,X.dot(w)*y)).values.reshape(len(y),1) w_grad=np.divide(yx,logywx).sum() #迭代 w=w+learning_rate*w_grad return w
2、将数据及标签带入上面定义的函数,学习率为0.5,迭代次数为1000次,输出训练好的参数,并将参数分类结果进行可视化
#输出训练好的参数 w=logistic_regression(data[["x1","x2","ones"]],data["label"],0.5,max_iter=1000) print(w) #可视化分类结果 x1=np.linspace(-6,6,50) x2=-(w[0]/w[1])*x1-w[2]/w[1] plt.figure(figsize=(8,8))#设置图片尺寸 plt.scatter(data_pos["x1"],data_pos["x2"],c="#E4007F",marker="^")#类别为1的数据绘制成洋红色 plt.scatter(data_neg["x1"],data_neg["x2"],c="#007979",marker="o")#类别为-1的数据绘制成深绿色 plt.plot(x1,x2,c="gray")#画出分类直线 plt.xlabel("$x_1$")#设置横轴标签 plt.ylabel("$x_2$")#设置纵轴标签 plt.title(‘手动实现的感知机模型‘) plt.xlim(-6,6)#设置横轴显示范围 plt.ylim(1,5)#设置纵轴显示范围 plt.show()
3、运行截图:
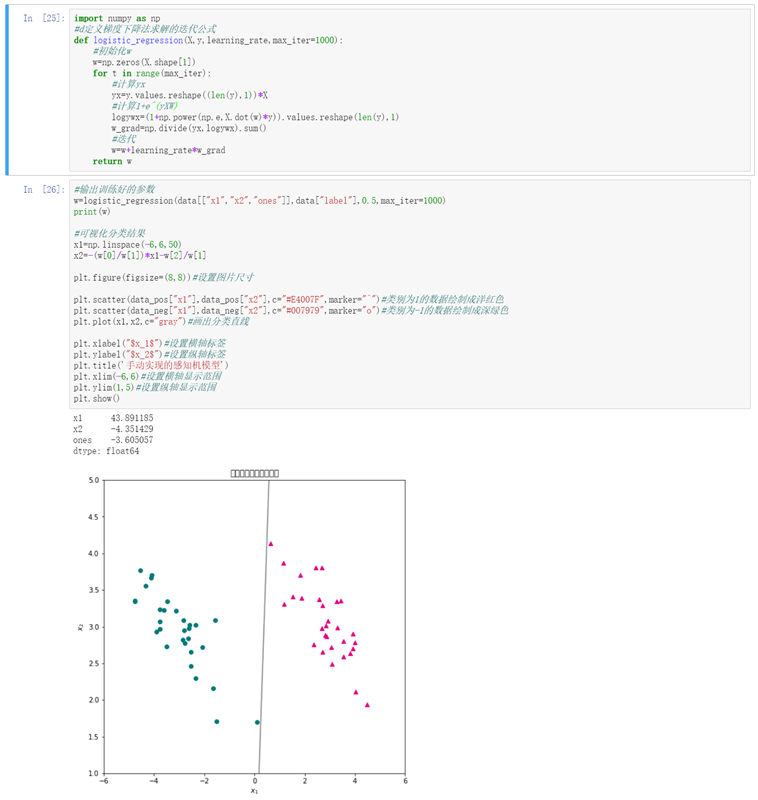
原文:https://www.cnblogs.com/hhjing/p/14341709.html