并查集(Union Find),从字面意思不太好理解这东西是个啥,但从名字大概可以得知与查询和集合有关,而实际也确实如此。并查集实际上是一种很不一样的树形结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。
之所以说并查集是一种“不一样”的树形结构,是因为一般的树形结构都是父节点指向子节点的,而并查集则是反过来,子节点指向父节点,并且这棵树会是一棵多叉树。
并查集可以高效的用来解决连接问题(Connectivity Problem),我们来看下面这样的一张图:
可以看到,该图中有很多的点,有些点之间有连接,而有些点之间则没有连接。那么此时就有一个问题是:这图中任意的两个点是否可能通过一条路径连接起来。对于这个问题,我们使用并查集就可以高效的求解,因为并查集可以非常快地判断网络中节点间的连接状态。这里的网络指的是广义的网络,例如用户之间形成的社交网络,有时候也叫做图。
并查集对于一组数据来说,主要支持两种操作:
union(p, q),把两个不相交的集合合并为一个集合。isConnected(p, q),查询两个元素是否在同一个集合中,也就是是否可以连接的。根据这两个操作,我们就可以定义出并查集的接口了,这是因为并查集可以有多种实现方式,这里定义接口来做统一抽象:
package tree.unionfind;
/**
* 并查集接口
*
* @author 01
* @date 2021-01-28
**/
public interface UnionFind {
/**
* 查询两个元素是否在同一个集合中
*
* @param p p
* @param q q
* @return true or false
*/
boolean isConnected(int p, int q);
/**
* 合并两个元素到同一个集合中
*
* @param p p
* @param q q
*/
void unionElements(int p, int q);
/**
* 并查集中的元素数量
*
* @return int
*/
int getSize();
}如果我们希望并查集的查询效率高一些,那么我们就可以侧重于查询操作,实现一个“Quick Find”性质的并查集。我们可以使用数组来表示并查集中的数据,数组中存放每个元素所在的集合编号,例如 0 和 1。而数组的索引则作为每个元素的 id,这样我们在查询的时候,只需要根据数组索引取出相应的两个元素的集合编号,判断是否相等就能得知这两个集合是否存储在同一集合中,也就知道这两个元素是否可以“连接”。具体如下图:
例如,传入的 p 和 q,分别是 1 和 3。那么根据数组索引找到的元素编号都为 1,此时就可以判断出这两个元素属于同一集合,也就代表这两个元素之间可以“连接”,反之同理。由于数组的特性,这个查询的时间复杂度就是 $O(1)$,我们就认为称这个并查集具有“Quick Find”性质。
合并操作也很简单,通过传入的 p 和 q,得到它们的集合编号。然后遍历数组,找其中一个集合编号,假定找的是 p 的集合编号,找到后将其更新为 q 的集合编号即可。当然,反过来也是可以的,这个没有特殊的规定。由于要遍历数组,因此合并操作的时间复杂度就是 $O(n)$。可见,“Quick Find”是牺牲了合并操作的效率。
具体的实现代码如下:
package tree.unionfind;
/**
* “Quick Find”性质的Union-Find
*
* @author 01
*/
public class UnionFind1 implements UnionFind {
/**
* “Quick Find”性质的Union-Find本质就是一个数组
*/
private final int[] ids;
public UnionFind1(int size) {
ids = new int[size];
// 初始化,每一个ids[i]指向自己所在的数组索引,因为此时没有合并的元素
for (int i = 0; i < size; i++) {
ids[i] = i;
}
}
@Override
public int getSize() {
return ids.length;
}
/**
* 查找元素p所对应的集合编号
* O(1)复杂度
*/
private int find(int p) {
if (p < 0 || p >= ids.length) {
throw new IllegalArgumentException("p is out of bound.");
}
return ids[p];
}
/**
* 查看元素p和元素q是否所属一个集合,这里的p和q就是表示的数组索引
* O(1)复杂度
*/
@Override
public boolean isConnected(int p, int q) {
// 只需要判断两个元素所属的集合编号是否相等即可
return find(p) == find(q);
}
/**
* 合并元素p和元素q所属的集合
* O(n) 复杂度
*/
@Override
public void unionElements(int p, int q) {
int pId = find(p);
int qId = find(q);
// 已经是属于同一集合
if (pId == qId) {
return;
}
// 合并过程需要遍历一遍所有元素,将两个元素的所属集合编号合并
for (int i = 0; i < ids.length; i++) {
if (ids[i] == pId) {
ids[i] = qId;
}
}
}
}有“Quick Find”自然就有“Quick Union”,“Quick Find”的查询和合并操作不是那么的平衡,时间复杂度相差得比较大,是完全牺牲了合并操作的性能。因此,这种并查集的实现思路并不常用,而“Quick Union”是相对来说更常用,以及更标准的实现思路。因为“Quick Union”是基于树的,虽然这棵树也可以使用数组来表示。
使用“Quick Union”思路实现并查集时,我们将每一个元素,看做是一个节点。但与普通的树形结构不同的是,并查集的树是子节点指向父节点的,在之前也提到过。如下: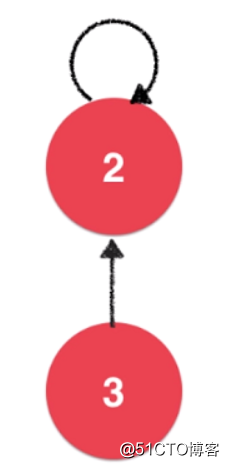
可以看到,3 这个子节点是指向它的父节点 2 的,而这个父节点是一个根节点则是会自己指向自己。接下来,我们先看看合并操作。如果我们要让元素 3 和元素 1 进行合并,只需要让元素 1 指向元素 3 的父节点元素 2 即可。如下所示: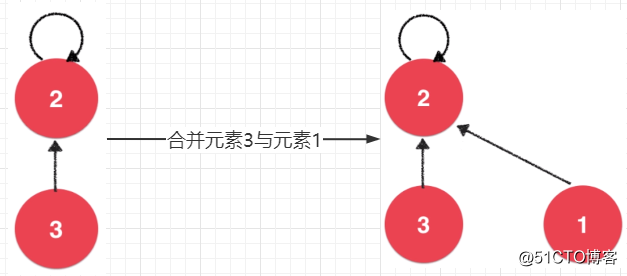
还有一种情况就是,合并另一棵树的子节点。例如,节点 5 有两个子节点 6 和 7,此时希望将节点 7 与之前的节点 2 进行合并。对于这种情况其实只需要将其父节点 5 与节点 2 进行合并即可。如下所示: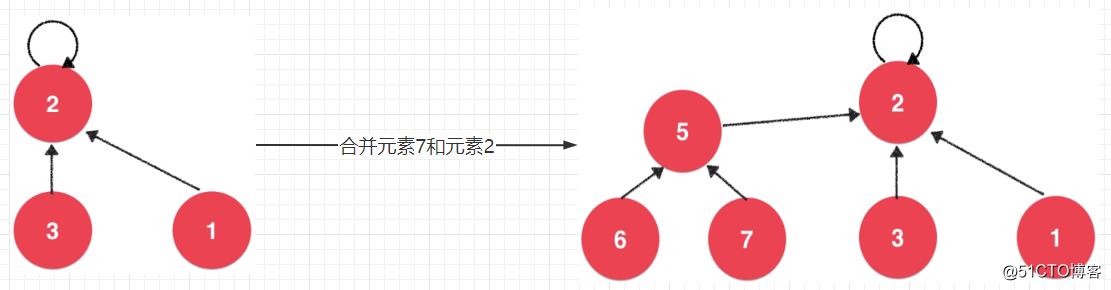
从上图可以看出,“Quick Union”的并查集在合并集合时,其实就是在合并两棵树,而一棵树就是在表示一个集合。理解这种表示集合的方式非常重要。属于同一个根节点的元素,我们就可以认为它们属于同一个集合。集合的合并就是树的合并,合并的方式是一棵树的根节点挂到另一棵树的根节点下,成为对方的子树。就像是一个集合与另一个集合合并后,成为对方的子集。
我们使用数组来表示树形结构的并查集时,子节点指向父节点的指针实际就是存储父节点的数组索引。而且在初始化后,未进行合并操作时,每个元素都是自己成为一棵树的根节点,代表不同的集合。也就是说此时会有多棵树,这种情况称之为森林结构,这也是为什么会存在合并两棵树的情况。如下所示:
对应的数组表示如下:
基于上图,如果我们此时合并 4 和 3 这两个元素,也就是将 4 的指针指向 3,3 成为 4 的父节点。如下:
那么只需要更新数组中索引为 4 的元素的值为 3 即可,因为子节点只需要存储父节点的数组索引,此时就完成了合并操作。如下所示:
我们再看看其余情况的合并操作: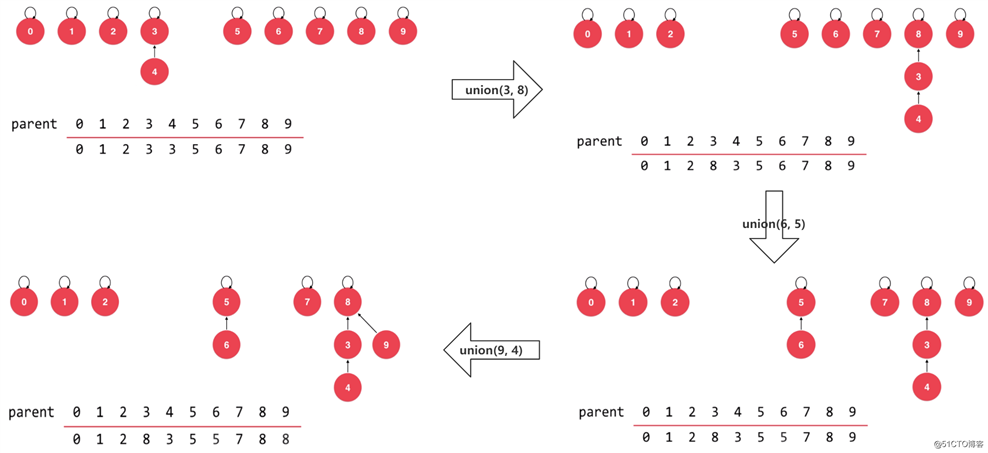
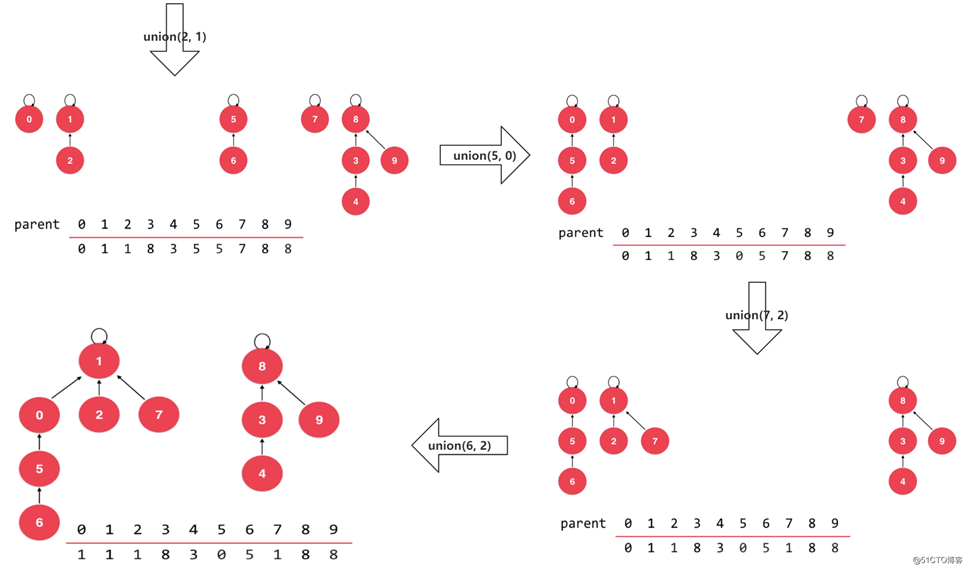
由于树的特性,此时并查集的查询操作时间复杂度就是 $O(h)$,$h$ 为树的高度。因为查询两个节点是否属于同一集合,就等同于查询这两个节点是否属于同一棵树。那么,就得找到这两个节点的根节点,判断是否是同一个节点,所以时间复杂度取决于树的高度。同理,合并操作也是一样的,因为 B 节点需要与 A 节点合并的话,那么就得找到 A 节点的根节点,并将自己挂载到该根节点下。
接下来,我们就实现“Quick Union”性质的并查集。代码如下:
package tree.unionfind;
/**
* “Quick Union”性质的Union-Find
*
* @author 01
*/
public class UnionFind2 implements UnionFind {
/**
* “Quick Union”性质的Union-Find,使用一个数组构建一棵指向父节点的树
* parent[i]表示第一个元素所指向的父节点
*/
private final int[] parent;
public UnionFind2(int size) {
parent = new int[size];
// 初始化,此时每一个parent[i]指向自己,表示每一个元素自己自成一颗树
for (int i = 0; i < size; i++) {
parent[i] = i;
}
}
@Override
public int getSize() {
return parent.length;
}
/**
* 查找过程, 查找元素p所对应的集合编号
* O(h)复杂度, h为树的高度
*/
private int find(int p) {
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of bound.");
}
// 不断去查询自己的父亲节点, 直到到达根节点
// 根节点的特点: parent[p] == p
while (p != parent[p]) {
p = parent[p];
}
return p;
}
/**
* 查看元素p和元素q是否所属一个集合
* O(h)复杂度, h为树的高度
*/
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
/**
* 合并元素p和元素q所属的集合
* O(h)复杂度, h为树的高度
*/
@Override
public void unionElements(int p, int q) {
// 找到p和q的根节点
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
// 将q的根节点挂载到p的根节点下,成为它的子节点
parent[pRoot] = qRoot;
}
}在上一小节中,我们实现了“Quick Union”性质的并查集,这也是并查集标准的实现方式。但这只是一个基础的实现,仍有许多优化空间。本小节就演示一下其中一种优化方法:基于size的优化。
在基础的“Quick Union”实现中,对 q 和 p 进行合并时,我们只是简单地把 q 的根节点挂载到 p 的根节点下,没有去判断另一棵树是什么形状的。此时在极端的情况下,并查集中的这棵树可能会退化成线性的时间复杂度: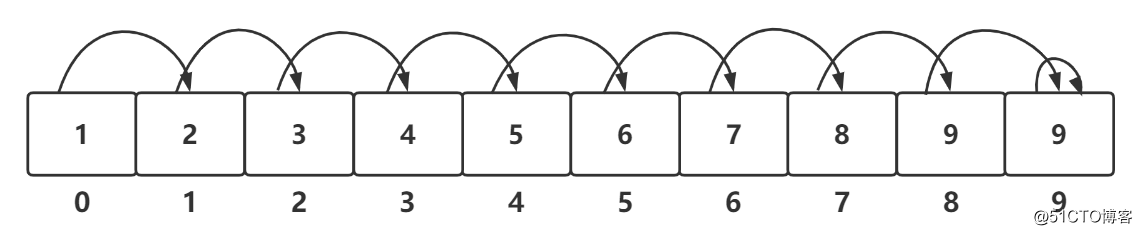
为了解决这个问题,我们需要在合并时,考虑当前这棵树的size,也就是需要判断一下树中的节点数量。通过这个节点数量来决定合并方向,将节点数量少的那棵树合并到节点数量多的那棵树上。如下所示: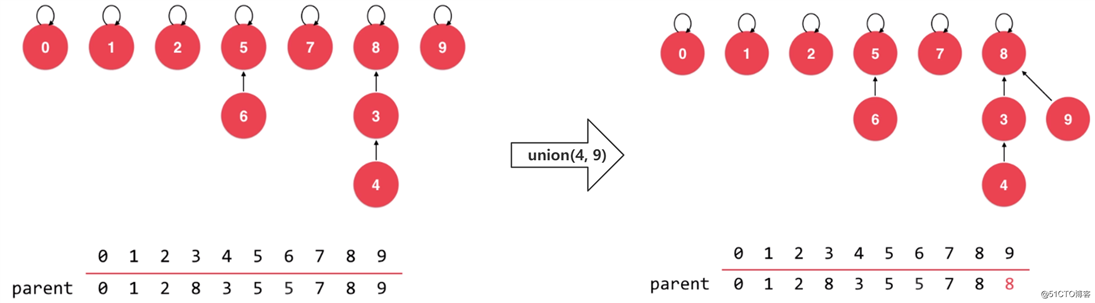
具体的实现代码如下:
package tree.unionfind;
/**
* 基于size优化的Union-Find
*
* @author 01
*/
public class UnionFind3 implements UnionFind {
/**
* parent[i]表示第一个元素所指向的父节点
*/
private final int[] parent;
/**
* sz[i]表示以i为根的集合中元素个数
*/
private final int[] sz;
public UnionFind3(int size) {
parent = new int[size];
sz = new int[size];
// 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
for (int i = 0; i < size; i++) {
parent[i] = i;
sz[i] = 1;
}
}
@Override
public int getSize() {
return parent.length;
}
/**
* 查找过程, 查找元素p所对应的集合编号
* O(h)复杂度, h为树的高度
*/
private int find(int p) {
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of bound.");
}
// 不断去查询自己的父亲节点, 直到到达根节点
// 根节点的特点: parent[p] == p
while (p != parent[p]) {
p = parent[p];
}
return p;
}
/**
* 查看元素p和元素q是否所属一个集合
* O(h)复杂度, h为树的高度
*/
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
/**
* 合并元素p和元素q所属的集合
* O(h)复杂度, h为树的高度
*/
@Override
public void unionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
// 根据两个元素所在树的元素个数不同判断合并方向
// 将元素个数少的集合合并到元素个数多的集合上
if (sz[pRoot] < sz[qRoot]) {
parent[pRoot] = qRoot;
sz[qRoot] += sz[pRoot];
} else {
parent[qRoot] = pRoot;
sz[pRoot] += sz[qRoot];
}
}
}在上一小节中,我们介绍了基于 size 的优化,这是一种最基础的并查集优化方式,从基于 size 的优化我们可以过渡到基于 rank 的优化。因为基于 size 的优化在某些极端情况下,仍然存在一些问题,另外基于 rank 的优化也是并查集的标准优化方式。
基于 size 的优化的问题就在于,我们希望树的高度尽量低,但是 size 小不意味着高度就低。而相较而言,rank 可以更好地衡量高度。因为这里的 rank 表示的是树的层级数量,而不是像 size 那样的节点数量。
我们来看一个例子: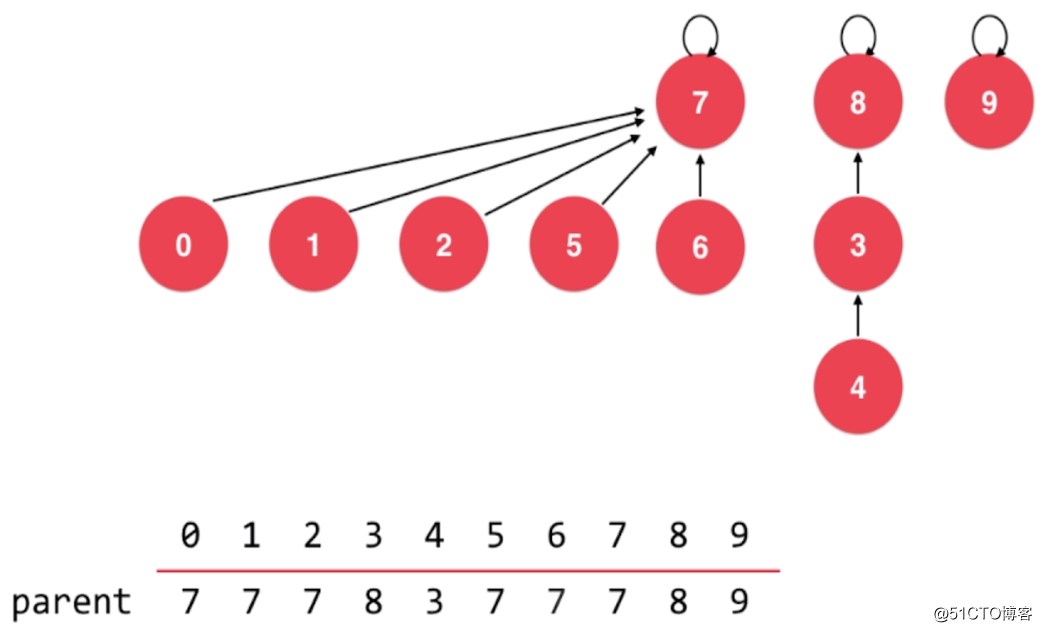
在这个例子中,我们要合并 4 和 2 这两个节点。从图中可以看到,2 所在的树共有 6 个节点,而 4 所在的树共有 3 个节点。如果使用的是基于 size 的优化,那么 size 小的要向 size 大的合并,4 所在的根节点 8 就需要挂到 2 所在的根节点 7 下。合并后,如下图所示: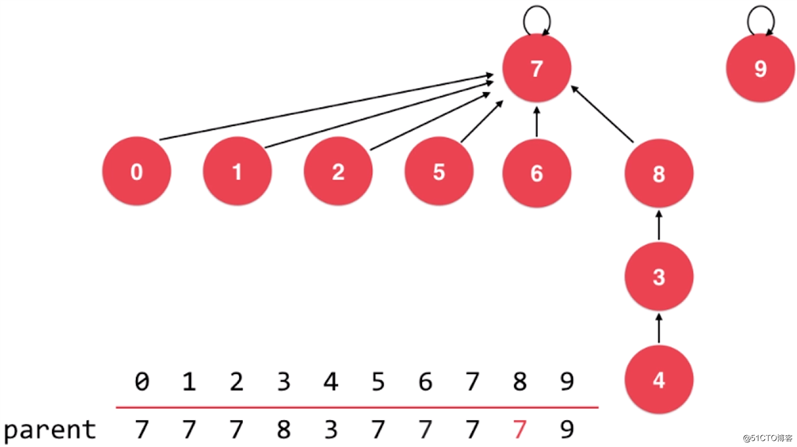
可以看到,在这种情况下,基于 size 的优化就不是最优的,合并后的树的高度反而变高了。所以更合理的做法应该是层数低的向层数高的合并,也就是 rank 小的向 rank 大的合并。在此例中,就应该是 2 所在的根节点 7 挂到 4 所在的根节点 8 下。如下图所示: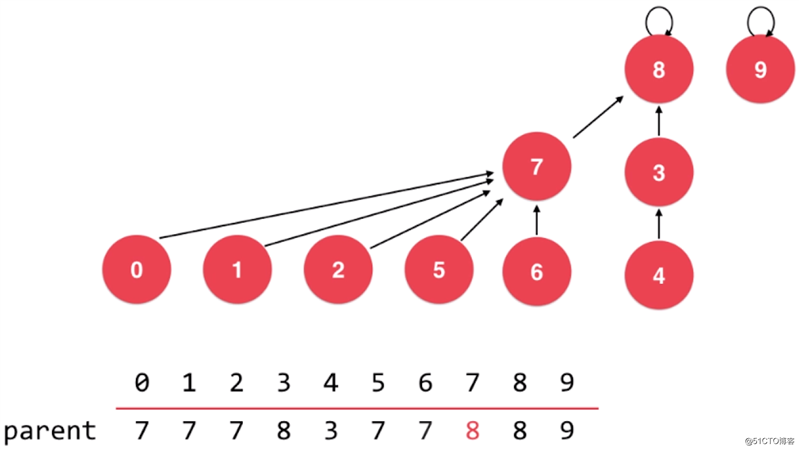
改进后,基于 rank 优化的并查集代码如下:
package tree.unionfind;
/**
* 基于rank优化的Union-Find
*
* @author 01
*/
public class UnionFind4 implements UnionFind {
/**
* rank[i]表示以i为根的集合所表示的树的层数(高度)
*/
private final int[] rank;
/**
* parent[i]表示第i个元素所指向的父节点
*/
private final int[] parent;
public UnionFind4(int size) {
rank = new int[size];
parent = new int[size];
// 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
for (int i = 0; i < size; i++) {
parent[i] = i;
rank[i] = 1;
}
}
@Override
public int getSize() {
return parent.length;
}
/**
* 查找过程, 查找元素p所对应的集合编号
* O(h)复杂度, h为树的高度
*/
private int find(int p) {
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of bound.");
}
// 不断去查询自己的父亲节点, 直到到达根节点
// 根节点的特点: parent[p] == p
while (p != parent[p]) {
p = parent[p];
}
return p;
}
/**
* 查看元素p和元素q是否所属一个集合
* O(h)复杂度, h为树的高度
*/
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
/**
* 合并元素p和元素q所属的集合
* O(h)复杂度, h为树的高度
*/
@Override
public void unionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
// 根据两个元素所在树的rank不同判断合并方向
// 将rank低的集合合并到rank高的集合上
if (rank[pRoot] < rank[qRoot]) {
// 被合并的树高度不会增加,不需要维护rank
parent[pRoot] = qRoot;
} else if (rank[qRoot] < rank[pRoot]) {
parent[qRoot] = pRoot;
} else {
// 层数相同,向任意一方合并即可
parent[pRoot] = qRoot;
// 然后需要维护一下rank的值,因为层数相同,被合并的树必然层数会+1
rank[qRoot] += 1;
}
}
}基于 rank 的优化其实在一般的情况下已经没什么问题了,而且也能得到一个比较好的性能,但在 rank 的基础上,我们仍然还可以再进一步的优化。这种优化方式叫:路径压缩。在下图中,虽然树的高度不同,但这几个并查集都是等价的: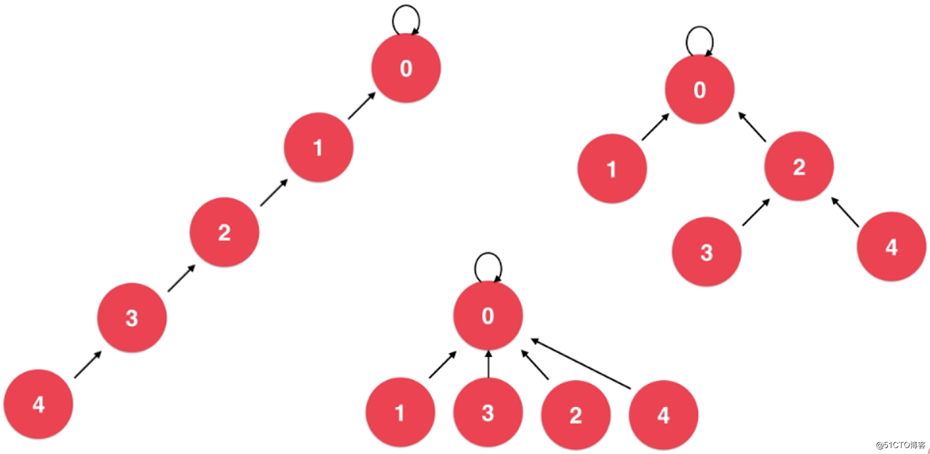
从上图中,明显可以看出左边的这棵树性能最低,因为其树的高度最高。因此,我们就知道树的高度是影响性能的一个主要原因。然而即便是基于 rank 的优化也无法避免数据量较大的情况下导致树的高度过高的问题,所以我们就得使用路径压缩这种优化方式来解决这个问题。
那么我们要如何进行路径压缩呢?其实只需要在 find 方法中增加一句代码即可:parent[p] = parent[parent[p]]。我们知道find 方法的主要逻辑是从指定的节点开始,一直循环往上找到它的根节点为止。
而这句代码的作用就是每次都将当前节点挂到其父节点的父节点上,这样就实现了查找过程就是一个压缩路径的过程。例如,我们要查找下图中,4 这个节点的根节点: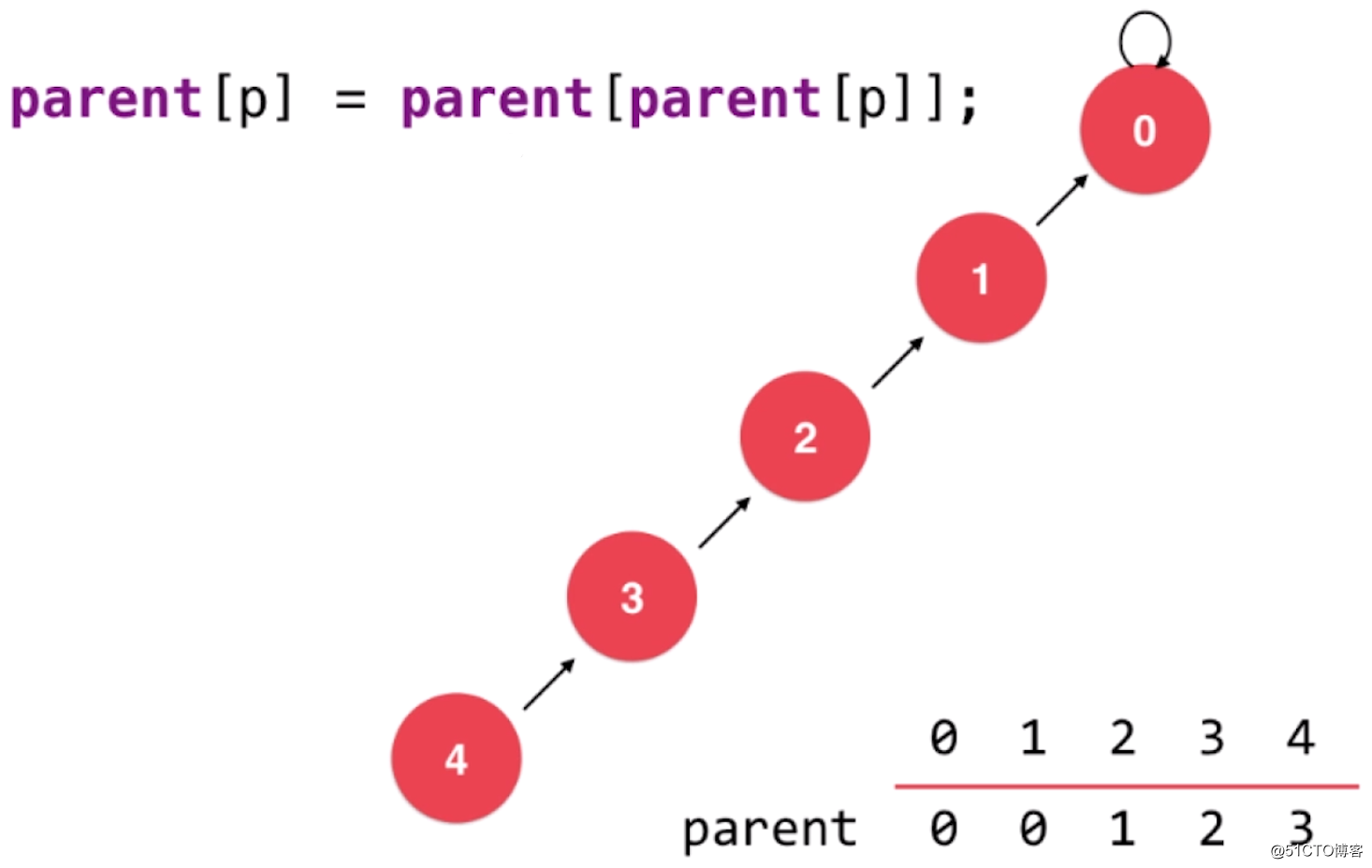
此时将这个节点挂载到其父节点的父节点上,就形成了这个样子: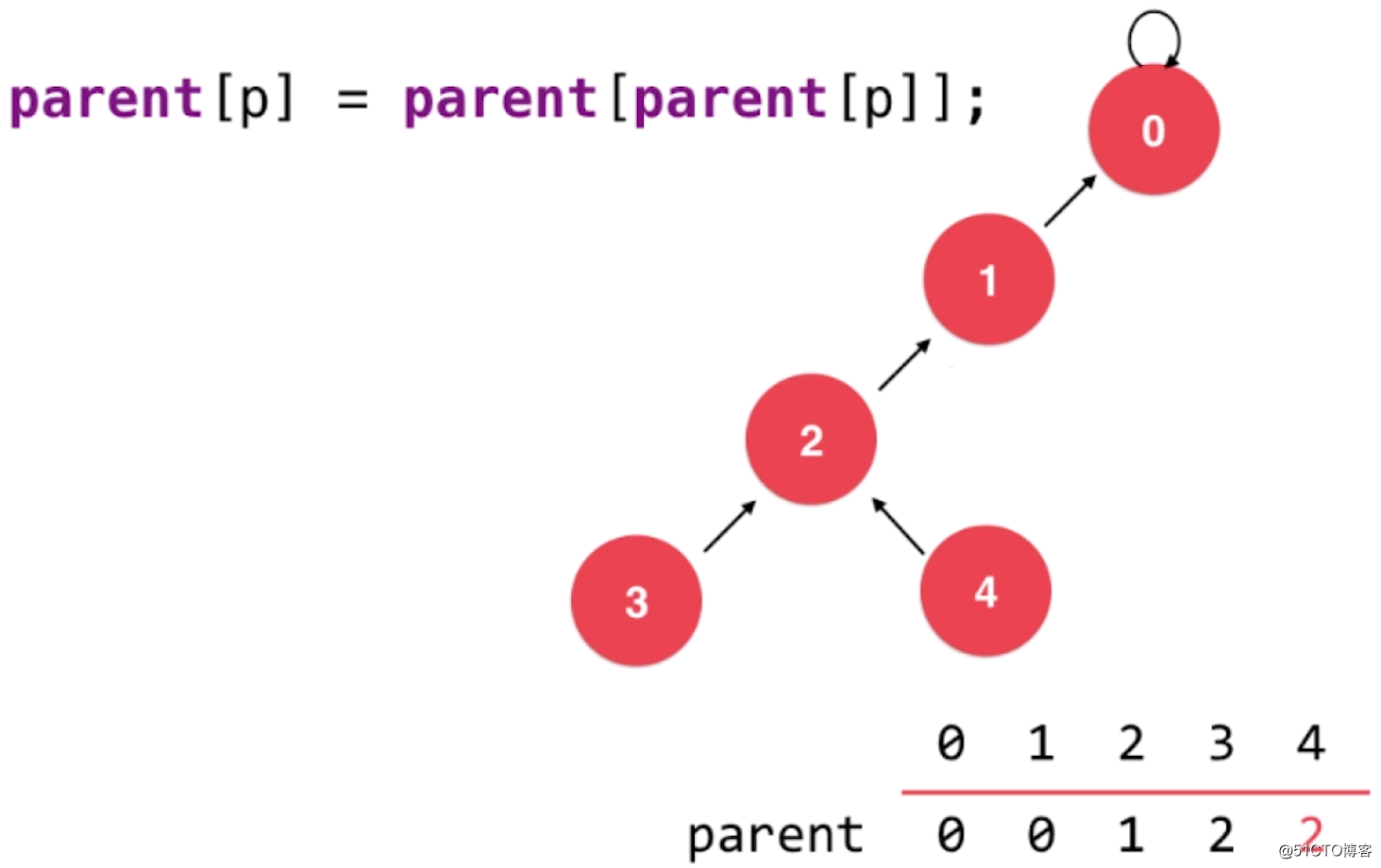
然后再继续这个循环,直到达到根节点,就完成了一次路径压缩: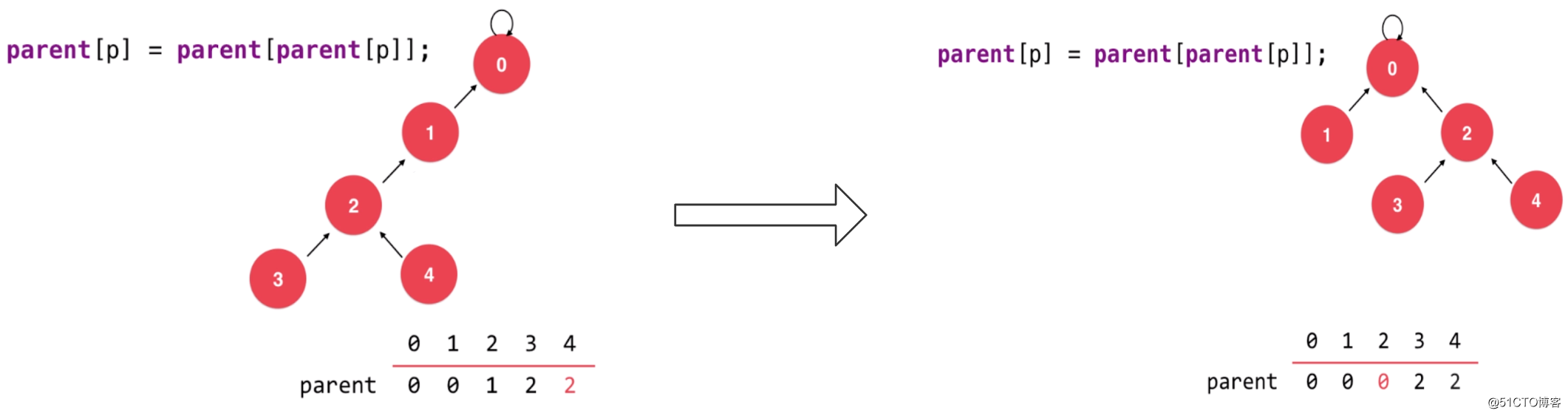
具体的实现代码如下:
package tree.unionfind;
/**
* 基于路径压缩优化的Union-Find
*
* @author 01
*/
public class UnionFind5 implements UnionFind {
/**
* rank[i]表示以i为根的集合所表示的树的层数
* 在后续的代码中, 我们并不会维护rank的语意, 也就是rank的值在路径压缩的过程中, 有可能不再表示树的层数值
* 这也是我们的rank不叫height或者depth的原因, 它只是作为比较的一个标准
*/
private final int[] rank;
/**
* parent[i]表示第i个元素所指向的父节点
*/
private final int[] parent;
public UnionFind5(int size) {
rank = new int[size];
parent = new int[size];
// 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
for (int i = 0; i < size; i++) {
parent[i] = i;
rank[i] = 1;
}
}
@Override
public int getSize() {
return parent.length;
}
/**
* 查找过程, 查找元素p所对应的集合编号
* O(h)复杂度, h为树的高度
*/
private int find(int p) {
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of bound.");
}
// 在查找根节点的过程中对路径进行压缩
while (p != parent[p]) {
// 每次都将当前节点挂到其父节点的父节点上
parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
}
/**
* 查看元素p和元素q是否所属一个集合
* O(h)复杂度, h为树的高度
*/
@Override
public boolean isConnected(int p, int q) {
return find(p) == find(q);
}
/**
* 合并元素p和元素q所属的集合
* O(h)复杂度, h为树的高度
*/
@Override
public void unionElements(int p, int q) {
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot) {
return;
}
// 根据两个元素所在树的rank不同判断合并方向
// 将rank低的集合合并到rank高的集合上
if (rank[pRoot] < rank[qRoot]) {
parent[pRoot] = qRoot;
} else if (rank[qRoot] < rank[pRoot]) {
parent[qRoot] = pRoot;
} else {
parent[pRoot] = qRoot;
// 维护一下rank的值
rank[qRoot] += 1;
}
}
}看到以上代码后,可能你会有一个疑问,为什么在压缩路径的过程中不用更新 rank 呢?事实上,这正是我们将这个变量叫做 rank 而不是叫诸如 depth 或者 height 的原因。因为这个 rank 只是我们做的一个标志当前节点排名的一个数字。当我们引入了路径压缩以后,维护这个深度的真实值会相对困难一些。
而实际上,这个 rank 的作用,只是在 union 的过程中,比较两个节点的深度。换句话说,我们完全可以不知道每个节点具体的深度,只要保证每两个节点深度的大小关系可以被 rank 正确表达即可。而这个 rank 确实可以正确表达两个节点之间深度的大小关系。
因为根据我们的路径压缩的过程,rank 高的节点虽然被抬了上来(深度降低),但是不可能降低到比原先深度更小的节点还要小。所以,rank 足以胜任比较两个节点的深度,进而选择合适的节点进行 union 这个任务。也就是说,此时 rank 更像是一个权重值,而不是表示树实际的深度。
在本小节所介绍的路径压缩算法,只能将一棵树压缩到高度为 3。那么有没有办法将一棵树压缩到高度只有 2 呢?如同下图这样: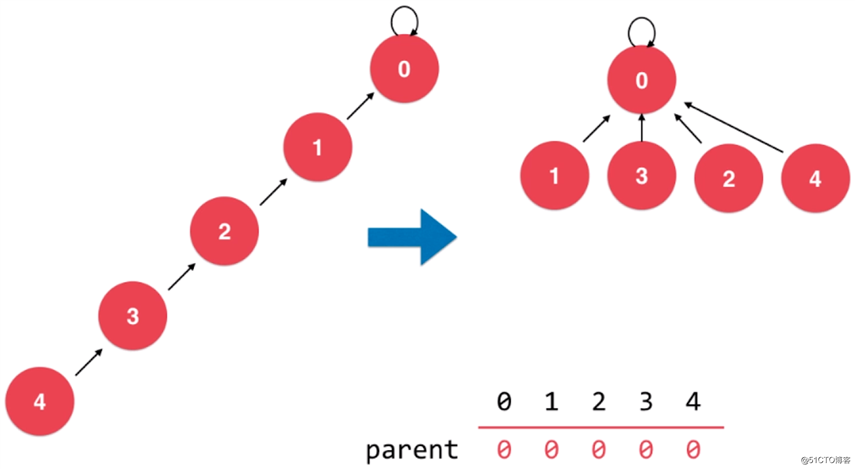
答案是有的,我们可以使用递归的方式,将树的高度压缩为 2 。但由于是使用递归实现的,递归开销比较大,所以其性能也不会比之前介绍的压缩方式性能高,甚至还不如。具体实现代码如下:
private int find(int p) {
if (p < 0 || p >= parent.length) {
throw new IllegalArgumentException("p is out of bound.");
}
// 递归实现路径压缩,将所有的节点直接压缩到根节点上,也就是每次压缩树的高度都会变成2
if (p != parent[p]) {
parent[p] = find(parent[p]);
}
return parent[p];
}最后,我们来编写一个简单的测试用例,对这几种方式实现的并查集进行性能测试,对比一下不同实现方式的性能差距。代码如下:
package tree.unionfind;
import java.util.Random;
public class UnionFindTests {
private static double testUnionFind(UnionFind uf, int m) {
int size = uf.getSize();
Random random = new Random();
long startTime = System.nanoTime();
for (int i = 0; i < m; i++) {
int a = random.nextInt(size);
int b = random.nextInt(size);
uf.unionElements(a, b);
}
for (int i = 0; i < m; i++) {
int a = random.nextInt(size);
int b = random.nextInt(size);
uf.isConnected(a, b);
}
long endTime = System.nanoTime();
return (endTime - startTime) / 1000000000.0;
}
public static void main(String[] args) {
int size = 1000000;
int m = 1000000;
UnionFind1 uf1 = new UnionFind1(size);
System.out.println("UnionFind1 : " + testUnionFind(uf1, m) + " s");
UnionFind2 uf2 = new UnionFind2(size);
System.out.println("UnionFind2 : " + testUnionFind(uf2, m) + " s");
UnionFind3 uf3 = new UnionFind3(size);
System.out.println("UnionFind3 : " + testUnionFind(uf3, m) + " s");
UnionFind4 uf4 = new UnionFind4(size);
System.out.println("UnionFind4 : " + testUnionFind(uf4, m) + " s");
UnionFind5 uf5 = new UnionFind5(size);
System.out.println("UnionFind5 : " + testUnionFind(uf5, m) + " s");
}
}输出结果如下:
UnionFind1 : 436.5402681 s
UnionFind2 : 1337.1119902 s
UnionFind3 : 0.0927705 s
UnionFind4 : 0.0725342 s
UnionFind5 : 0.0553162 s原文:https://blog.51cto.com/zero01/2609695