一、学习资料:
北京博雅数据酷客平台大讲堂:http://cookdata.cn/auditorium/course_room/10015/
案例连接:http://cookdata.cn/note/view_static_note/61f373ccecf93d7ecb7fd03e11e7ff3e/
二、分布梳理
分类决策树Python实现
1、定义决策树节点
2、基尼系数计算
3、分类决策树生成
4、使用Networkx将决策树可视化
5、决策树的决策边界
6、实现决策树的预测函数
三、代码实现
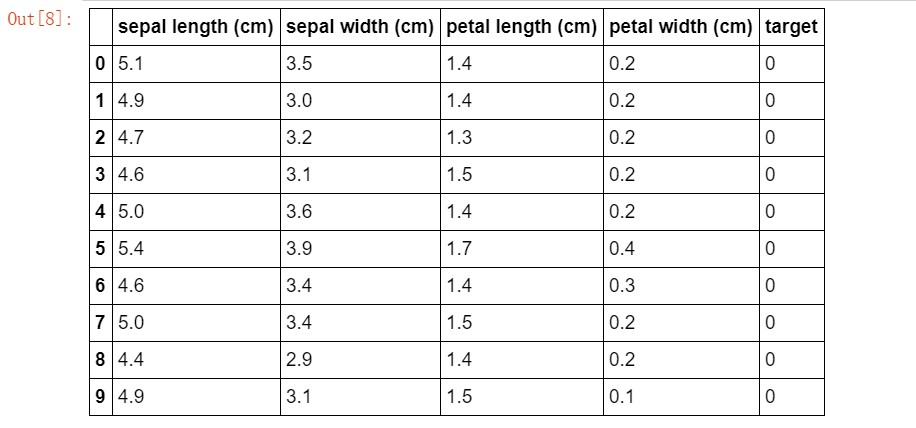
首先加载一份鸢尾花数据用于测试,在Sklearn中可以使用datasets.load_iris方法直接加载数据集。鸢尾花数据集包含150个鸢尾花样本,每个样本包含四个特征和一个类别标签。
from sklearn.datasets import load_iris import pandas as pd iris=load_iris() iris_df=pd.DataFrame(data=iris.data,columns=iris.feature_names) iris_df["target"]=iris.target iris_df.head() iris_df.columxs=["sepal_len","sepal_width","petal_len","petal_width","target"] X_iris=iris_df.iloc[:,:-1] y_iris=iris_df["target"] iris_df.head(10) #显示默认行数
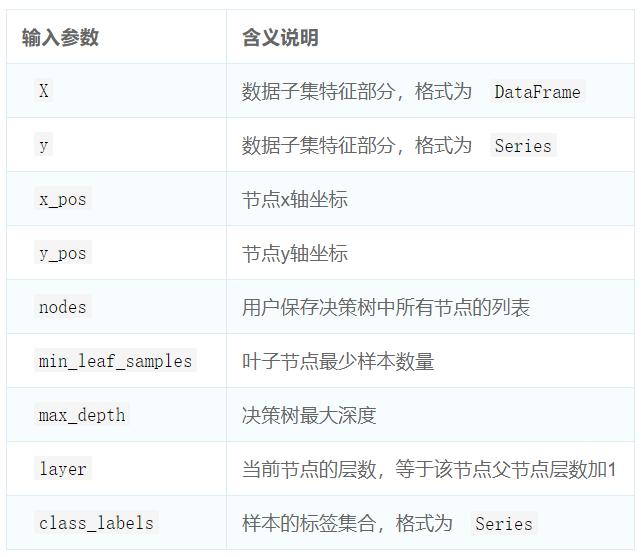
1、定义决策树节点。创建一个表示决策树节点的类TreeNode。决策树节点需要存储的最重要的信息为当前节点代表的特征。如果节点是非叶子节点,还需要存储做儿子节点left和右儿子节点right。
class TreeNode: def _init_(self,x_pos,y_pos,layer,class_labels=[0,1,2]): self.f=None #当前节点的切分特征 self.v=None #当前节点的切分点 self.left=None #左儿子节点 self.right=None #右儿子节点 self.pos=(x_pos,y_pos)#节点坐标,进行可视化 self.label_dist=None #当前节点样本的类分布 self.layer=layer self.class_labels=class_labels def _str_(self):#打印节点信息,可视化时的节点标签 if self.f!=None: return self.f+"\n<="+str(round(self.v,2)) else: return str(self.label_dist)+"\n("+str(np.sum(self.label_dist))+")"
2、基尼系数计算

import numpy as np def gini(y): #输入标签序列,返回基尼系数 return 1-np.square(y.value_counts()/len(y)).sum()
3、分类决策树生成
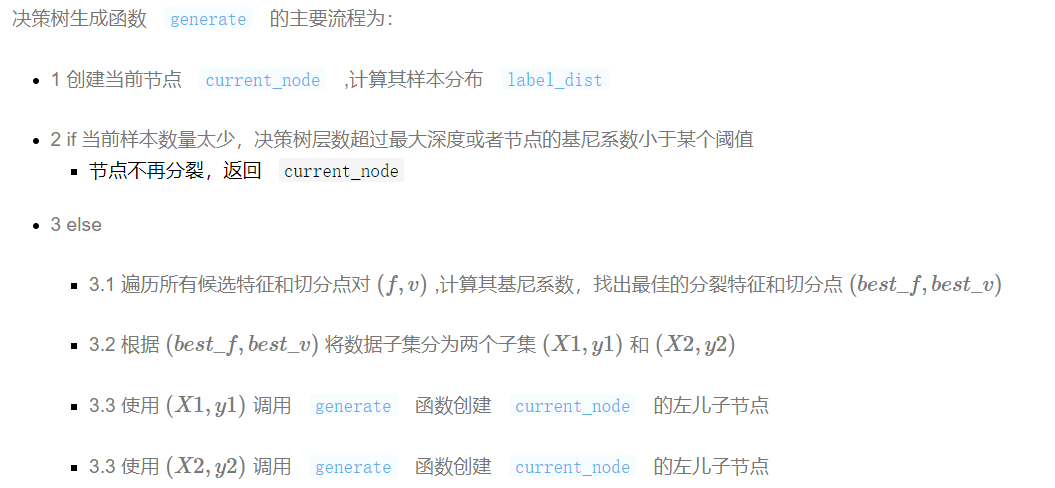
def generate(X,y,x_pos,y_pos,nodes,min_leaf_samples,max_depth,layer,class_labels): current_node = TreeNode(x_pos,y_pos,layer,class_labels)#创建节点对象 current_node.label_dist = [len(y[y==v]) for v in class_labels] #当前节点类样本分布 nodes.append(current_node) if(len(X) < min_leaf_samples or gini(y) < 0.1 or layer > max_depth): #判断是否需要生成子节点 return current_node max_gini,best_f,best_v = 0,None,None for f in X.columns: #特征遍历 for v in X[f].unique(): #取值遍历 y1,y2 = y[X[f] <= v],y[X[f] > v] if (len(y1) >= min_leaf_samples and len(y2) >= min_leaf_samples): imp_descent = gini(y)-gini(y1)*len(y1)/len(y)-gini(y2)*len(y2)/len(y) #****计算不纯度变化****# if imp_descent > max_gini: max_gini,best_f,best_v = imp_descent,f,v current_node.f,current_node.v = best_f,best_v if(current_node.f != None): current_node.left = generate(X[X[best_f] <= best_v],y[X[best_f] <= best_v],x_pos-(2**(max_depth-layer)),y_pos -1,nodes,min_leaf_samples,max_depth,layer + 1,class_labels) current_node.right = generate(X[X[best_f] > best_v],y[X[best_f] > best_v],x_pos+ (2**(max_depth-layer)),y_pos -1,nodes,min_leaf_samples,max_depth,layer + 1,class_labels) return current_node def decision_tree_classifier(X,y,min_leaf_samples,max_depth): nodes = [] root = generate(X,y,0,0,nodes,min_leaf_samples=min_leaf_samples,max_depth=max_depth,layer=1,class_labels=y.unique()) return root,nodes
4、使用Networkx将决策树可视化
#编写一个函数,将训练得到的决策树转换成 Networkx 中的网络对象 G def get_networkx_graph(G, root): if root.left != None: G.add_edge(root, root.left) #在当前节点和左儿子节点之间建立一条边,加入G get_networkx_graph(G, root.left) #对左儿子执行同样操作 if root.right != None: G.add_edge(root, root.right) #在当前节点和左儿子节点之间建立一条边,加入G get_networkx_graph(G,root.right)#对右儿子执行同样操作 #在决策树生成函数中,已经计算了节点的坐标。现在我们实现一个函数,输入节点集合,返回其位置布局字典对象。 def get_tree_pos(G): pos = {} for node in G.nodes: pos[node] = node.pos return pos #在决策树中,如果是叶子节点,则根据其预测类别显示不同颜色。如果是非叶子节点,则显示灰色。 def get_node_color(G): color_dict = [] for node in G.nodes: if node.f == None: #叶子节点 label = np.argmax(node.label_dist) if label%3 == 0: color_dict.append("#007979") #深绿色 elif label%3 == 1: color_dict.append("#E4007F") #洋红色 else: color_dict.append("blue") else: color_dict.append("gray") return color_dict #在鸢尾花数据集上训练决策树,然后将学习到的决策树绘制出来。 import matplotlib.pyplot as plt import networkx as nx %matplotlib inline #1训练决策树 root,nodes = decision_tree_classifier(X_iris,y_iris,min_leaf_samples=10,max_depth=4) #2将决策树进行可视化 fig, ax = plt.subplots(figsize=(9, 9)) #2.1将图的大小设置为 9×9 graph = nx.DiGraph() #2.2 创建 Networkx 中的网络对象 get_networkx_graph(graph, root) #**** 2.3将决策树转换成 Networkx 的网络对象****# pos = get_tree_pos(graph) #****2.4 获取节点的坐标****# # 2.5 绘制决策树 nx.draw_networkx(graph,pos = pos,ax = ax,node_shape="o",font_color="w",node_size=5000,node_color=get_node_color(graph)) plt.box(False) #去掉边框 plt.axis("off")#不显示坐标轴
5、决策树的决策边界
import seaborn as sns #筛选两列特征 feature_names = ["petal_len","petal_width"] X = iris_df[feature_names] y = iris_df["target"] #训练决策树模型 tree_two_dimension, nodes = decision_tree_classifier(X,y,min_leaf_samples=10,max_depth=4) fig, ax = plt.subplots(figsize=(9, 9)) #设置图片大小 sns.scatterplot(x = X.iloc[:,0], y = X.iloc[:,1],ax = ax,hue = y) #绘制样本点 scatterplot #遍历决策树节点,绘制划分直线 for node in nodes: if node.f == X.columns[0]: ax.vlines(node.v,X.iloc[:,1].min(),X.iloc[:,1].max(),color="gray") #****如果节点分裂特征是 petal_len ,则绘制竖线****# elif node.f == X.columns[1]: ax.hlines(node.v,X.iloc[:,0].min(),X.iloc[:,0].max(),color="gray") #如果节点分裂特征是 petal_width ,则绘制水平线
6、实现决策树的预测函数
from sklearn.metrics import confusion_matrix import seaborn as sns import matplotlib.pyplot as plt fig, ax = plt.subplots(figsize=(9,9)) # 设置正常显示中文 sns.set(font=‘SimHei‘) # 绘制热力图 confusion_matrix = confusion_matrix(y_pred,iris_df["target"])#****计算混淆矩阵****# ax = sns.heatmap(confusion_matrix,linewidths=.5,cmap="Greens", annot=True, fmt=‘d‘,xticklabels=iris.target_names, yticklabels=iris.target_names) ax.set_ylabel(‘真实‘) ax.set_xlabel(‘预测‘) ax.xaxis.set_label_position(‘top‘) ax.xaxis.tick_top() ax.set_title(‘混淆矩阵热力图‘)
原文:https://www.cnblogs.com/hhjing/p/14350450.html