最小生成树普通理解

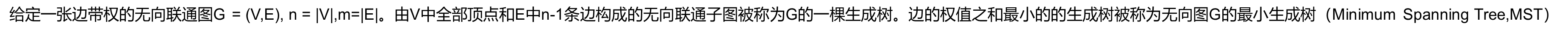
 特点：

 以上都是来自今天学长的内容，我觉得讲的超级好而且ppt内容也挺详细！！

实现最小生成树具有两种方法：

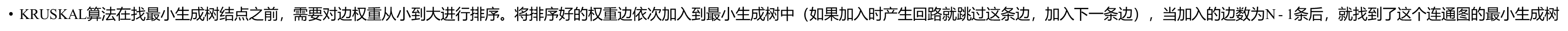
int getf(int x)
{
return x==f[x]?x:f[x]=getf(f[x]); //并查集的路径压缩的实现部分
}
const int inf=-0x3f3f3f3f;
void kruskal(int n,int m)
{
ans=0,num=0;
for(int i=1;i<=n;i++)
{
f[i]=i;  //初始化f数组 便于并查集后续使用
}
sort(a+1,1+m+a,cmp);  // 对边的长度进行一次排序，便于选择边
for(int i=1;i<=m;i++)
{
if(getf(a[i].u)!=getf(a[i].v))  //判断两个点的根节点是否相同 如果相同则代表已经有最短的路 如果不相同则代表此时是最短的，需要加入
{
ans+=a[i].w;
f[getf(a[i].v)]=getf(a[i].u);//个人的wa点 需要根节点是对方的根节点 并查集合并出了问题
num++;
}
if(num==n-1)
{
break;
}
}
}

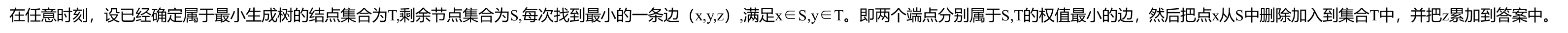
int n, m, G[maxn][maxn], vis[maxn], d[maxn];
void Prim(int n, int m) {
memset(vis, 0, sizeof(vis));
int index = 1; // 当前加入到小树的顶点
int res = 0; // 存放结果
vis[index] = 1;
for(int i = 1; i <= n; i++) // 更新这个点到其他点的距离
d[i] = G[index][i];
for(int i = 1; i < n; i++) { // 执行 n - 1 次， 找剩下的n - 1 个点
int minn = inf;
for(int j = 1; j <= n; j++) { // 找出未加入小树且 d 最小的点
if(!vis[j] && d[j] < minn) {
minn = d[j];
index = j;
}
}
if(minn == inf) { // 如果没有找到， 说明不存在最小生成树
puts("?");
return ;
}
res += minn; // 累加答案
vis[index] = 1; // 将这个点加入最小生成树中
for(int j = 1; j <= n; j++) { // 更新这个点加入后，当前这棵小树到未加入的点的最近距离
if(!vis[j] && d[j] > G[index][j]) d[j] = G[index][j];
}
}
printf("%d\n", res);
}

需要多刷刷题 才能补上自己和大佬的差距

最小生成树普通理解

原文：https://www.cnblogs.com/xyisreallycuteeee/p/14353658.html