[CS231n]SVM and Softmax

回顾

上一讲是\(KNN\)算法，是惰性算法，他不需要显示的构建模型，抽取特征，他只是在构建的时候需要找到那个就去找到跟他最近邻的数据，基本不需要训练，但是预测的时候是很慢的。\(Train~O(1),Predict~O(n)\)随着样本增加，其复杂度是线性增加的，但是随着维度的增加，其样本数是呈指数爆炸增长的，\(KNN\)算法的性能是比较差的。在训练集较少的情况下可以使用交叉验证方法来选取\(K\),来尽可能减少偶然误差，评估模型的性能。

SVM

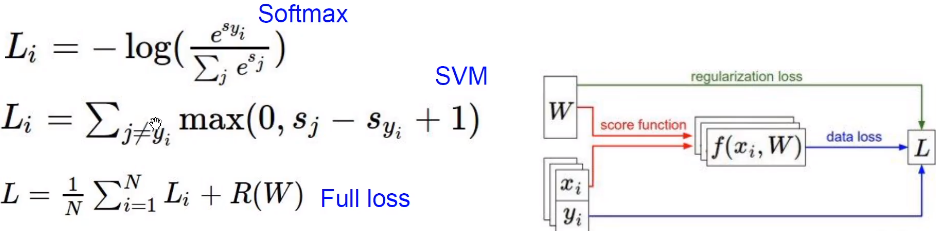
损失函数：说明了目前这个分类器的工作情况

我们设有\(x_i~s~image~and~y_i~s(integer)~label\)则有

这里\(f(x_i,W),y_i\)就是把分数和每一个具体的标签进行比较，然后对所有的损失函数值取平均值。

Hinge loss

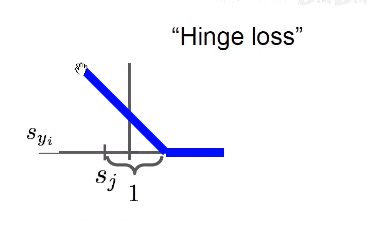
Eg:

这里对于猫的计算是\(max(0,5.1-3.2+1)+max(0,-1.7-3.2+1)=2.9\)

这里并没有对自生做这个计算，( 实际上，就算对自生做这个处理，也只是，对每一项的 loss加上了 1，并不会影响最终的结果，因为我们在这里看的是二者相对的值。)铰链损失函数会惩罚分数差1以上的项目，对于其他不进行惩罚。

Q1：如果汽车的分值发生了一点的变化？

并不会改变，因为1这个值的存在。

实际上1这个值是有讲究的，我们并不关心这个值的绝对的大小，而是相对的大小，1其实是单位1的意思。

Q2:最小、最大值是多少？

0-正无穷

Q3:在一开始\(W\)很小所以\(s->0\)那么\(loss\)值是多少？

应该是分类错误的类别的个数

Q4:在计算的时候加上了计算正确的类别？ 同上正文所讲

Q5:如果平均而不是求和？ 只是改了一个常数无影响

Q6:使用了平方损失函数？ 惩罚项被放大了

def L_i_vectorized(x, y, w):
    scores = W.dot(x)
    margins = sp.maximum(0, scores - scores[y] + 1)
    margins[y] = 0  # 这里是因为在上一步其把自身也减去了
    loss_i = np.sum(margins)
    return loss_i

如果\(loss=0\):

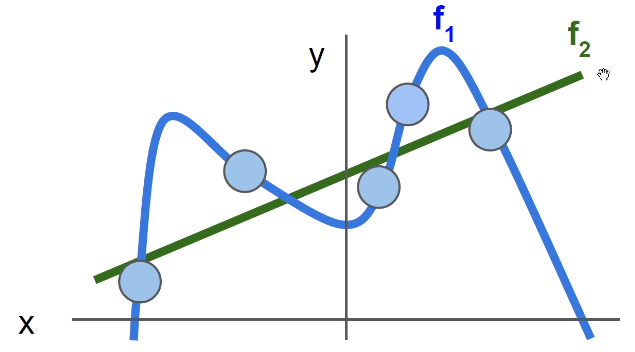
同一个损失函数可以对应于很多个不同的\(W\)，这里引入正则化，防止过拟合。

正则化让模型更加简单(drop out,batch normalization……)，让其在测试集上可以更好的泛化。显然下图\(f_2\)更加好

Softmax Classifier

先用指数函数的形式变成正数，接下来归一化处理

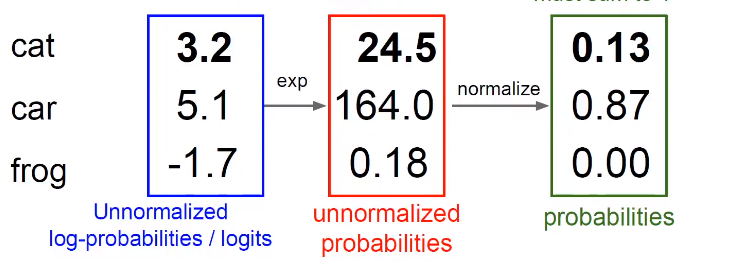
softmax把分数变成了概率，softmax不需要权重，本质进行了数学的运算。

然后再构造交叉熵损失函数，表示混乱程度，或者叫对数似然损失函数(details in CS229)

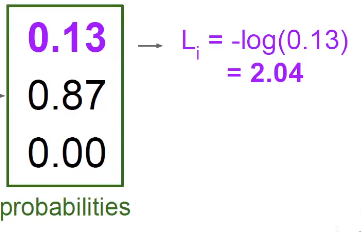
想要得到全部分类正确的概率就是把三个分类正确的概率乘起来，那么实际上就是在把各自的log加起来，这样做把一个非常小的概率转换成了一个比较好的值，我们希望对数的值最大化。

那么这个\(Loss\)表示为：

优化

[CS231n]SVM and Softmax

原文：https://www.cnblogs.com/ubiosturing/p/14354525.html