
这个分基本上和爆零没什么区别
只会打无脑暴力,高分暴力也不会
\(T1\) 写了一个随机化贪心拿了 \(20\),\(T2\) 水了一个 \(prufer\) 的分
写 \(T2\) 的时候居然认为边双是有向图的概念,暴搜也没有打出来
明天有一天整理的时间,要好好调整状态
毕竟放假之前最多也只有三次考试了
首先要了解什么是霍尔定理
设 \(M(U)\) 为与 \(U\) 中的点相连的点集,一个二分图 \(U,V(|U|<=|V|)\)存在完美匹配,满足对于任意点集 \(x \in U\)都有 |\(M(X)|>=|X|\)
因为要去枚举每一个子集,所以复杂度是 \(3^n\) 的
但是可以证明在题目条件下,只需要对每个左边的连续区间验证霍尔定理
考虑反证法,假如我们左边选了很多段连续区间,只考虑两段的情况,其余情况是类似的
先把所有没有和左边点相连的右边点去掉,那么对于每个左边的连续区间,与其相邻的右边点也是一个连续区间
那么我们分两种情况讨论:
\(1\):左边两段在右边的对应点是两段区间
如果左边两段分别验证霍尔定理都合法,那么左边这两段的并也一定合法
\(2\):左边两段在右边的对应点是一段区间
那么我们考虑把左边两段中间的点也选上,根据条件右边的点不会变多,这样的限制显然更紧
所以没有必要选择左边不连续的多段验证霍尔定理
只需要枚举 \(n^2\) 个区间就可以了
先把所有询问按照左端点从小到大排序
因为区间没有包含关系,那么排完序之后左右端点一定都是单调递增的,那么就可以用前缀和处理
设 \(a[i]\) 为石子个数的前缀和 ,\(b[i]\) 为每一次操作中实际选择的石子的前缀和
注意这里是实际选择的,而不是题目中要求选择的
因为实际选择的一定要满足霍尔定理,因为你已经选了这些了
但是题目中要求的你不一定全选
对于没有被询问包含的石子,要把它们的个数置成 \(0\),否则会影响结果
那么根据霍尔定理对于任意的 \(i \leq j\) ,必定存在 \(b_j-b_{i-1} \leq a_{r[j]}-a_{l[i]-1}\)
即\(b_j-a_{r[j]} \leq b_{i-1}-a_{l[i]-1}\)
此时左边和右边分别只有 \(j\) 和 \(i\) ,可以分开考虑
设 \(s_i=b_i-a_{r[i]},t_i=b_{i-1}-a_{l[i]-1}\)
即对于任意的 \(i \leq j\),都有 \(s_j \leq t_i\)
将询问按照时间排序处理
设当前询问在按照左端点排序时的排名为 \(p\)
当前的答案就是区间 \([1,p]\) 中 \(t\) 的最小值减去区间 \([p,m]\)中 \(s\) 的最大值
还要和想要的石子个数取一个 \(min\)
考虑当前答案会对 \(s\) 和 \(t\) 数组造成什么影响
对于 \(s\),要在区间 \([p,m]\) 加上 \(ans\)
对于 \(t\),要在区间 \([p+1,m]\) 加上 \(ans\)
对于左右端点都在 \([p+1,m]\)的区间,因为都加上了 \(ans\),所以减完之后关系不会改变
对于左右端点都在 \([1,p-1]\)的区间,当前的答案不会影响到它们,所以也不用考虑
我们要考虑的只是左端点在 \([1,p]\) ,右端点在 \([p,m]\) 的区间
我们加上答案后不能违背霍尔定理,所以答案不能超过区间 \([1,p]\) 中 \(t\) 的最小值减去区间 \([p,m]\)中 \(s\) 的最大值
不要忘了更新 \(s\) 和 \(t\) 数组
这个东西拿线段树维护一下就行了
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<‘0‘ || ch>‘9‘){
if(ch==‘-‘) fh=-1;
ch=getchar();
}
while(ch>=‘0‘ && ch<=‘9‘){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=1e6+5;
int n,m,sum[maxn],a[maxn];
struct jie{
int l,r,k,id,rk;
}b[maxn];
bool cmp(rg jie aa,rg jie bb){
return aa.l<bb.l;
}
bool cmp2(rg jie aa,rg jie bb){
return aa.id<bb.id;
}
struct trr{
int l,r,lazt,lazs,maxs,mint,siz;
}tr[maxn];
void push_up(rg int da){
tr[da].maxs=std::max(tr[da<<1].maxs,tr[da<<1|1].maxs);
tr[da].mint=std::min(tr[da<<1].mint,tr[da<<1|1].mint);
}
void updats(rg int da,rg int val){
tr[da].lazs+=val;
tr[da].maxs+=val;
}
void updatt(rg int da,rg int val){
tr[da].lazt+=val;
tr[da].mint+=val;
}
void push_down(rg int da){
if(tr[da].lazs){
updats(da<<1,tr[da].lazs);
updats(da<<1|1,tr[da].lazs);
tr[da].lazs=0;
}
if(tr[da].lazt){
updatt(da<<1,tr[da].lazt);
updatt(da<<1|1,tr[da].lazt);
tr[da].lazt=0;
}
}
void build(rg int da,rg int l,rg int r){
tr[da].l=l,tr[da].r=r,tr[da].siz=r-l+1;
if(tr[da].l==tr[da].r){
tr[da].maxs=-sum[b[l].r];
tr[da].mint=-sum[b[l].l-1];
return;
}
rg int mids=(l+r)>>1;
build(da<<1,l,mids);
build(da<<1|1,mids+1,r);
push_up(da);
}
void xgt(rg int da,rg int l,rg int r,rg int val){
if(tr[da].l>=l && tr[da].r<=r){
updatt(da,val);
return;
}
push_down(da);
rg int mids=(tr[da].l+tr[da].r)>>1;
if(l<=mids) xgt(da<<1,l,r,val);
if(r>mids) xgt(da<<1|1,l,r,val);
push_up(da);
}
void xgs(rg int da,rg int l,rg int r,rg int val){
if(tr[da].l>=l && tr[da].r<=r){
updats(da,val);
return;
}
push_down(da);
rg int mids=(tr[da].l+tr[da].r)>>1;
if(l<=mids) xgs(da<<1,l,r,val);
if(r>mids) xgs(da<<1|1,l,r,val);
push_up(da);
}
int cxt(rg int da,rg int l,rg int r){
if(tr[da].l>=l && tr[da].r<=r) return tr[da].mint;
push_down(da);
rg int mids=(tr[da].l+tr[da].r)>>1,nans=0x3f3f3f3f;
if(l<=mids) nans=std::min(nans,cxt(da<<1,l,r));
if(r>mids) nans=std::min(nans,cxt(da<<1|1,l,r));
return nans;
}
int cxs(rg int da,rg int l,rg int r){
if(tr[da].l>=l && tr[da].r<=r) return tr[da].maxs;
push_down(da);
rg int mids=(tr[da].l+tr[da].r)>>1,nans=-0x3f3f3f3f;
if(l<=mids) nans=std::max(nans,cxs(da<<1,l,r));
if(r>mids) nans=std::max(nans,cxs(da<<1|1,l,r));
return nans;
}
int cf[maxn];
int main(){
n=read();
for(rg int i=1;i<=n;i++) a[i]=read();
m=read();
for(rg int i=1;i<=m;i++){
b[i].l=read(),b[i].r=read(),b[i].k=read(),b[i].id=i;
cf[b[i].l]++,cf[b[i].r+1]--;
}
std::sort(b+1,b+1+m,cmp);
for(rg int i=1;i<=m;i++) b[i].rk=i;
for(rg int i=1;i<=n+1;i++) cf[i]+=cf[i-1];
for(rg int i=1;i<=n;i++) if(cf[i]==0) a[i]=0;
for(rg int i=1;i<=n;i++) sum[i]=sum[i-1]+a[i];
build(1,1,m);
std::sort(b+1,b+1+m,cmp2);
rg int tmp=0,wz;
for(rg int i=1;i<=m;i++){
wz=b[i].rk;
tmp=std::min(b[i].k,cxt(1,1,wz)-cxs(1,wz,m));
xgs(1,wz,m,tmp);
printf("%d\n",tmp);
if(wz+1<=m) xgt(1,wz+1,m,tmp);
}
return 0;
}
咕咕咕
首先,我们可以证明,答案的环会包含所有左上角到关键点左上角的最短路
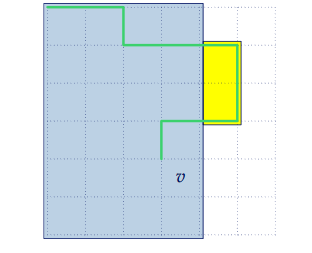
如图,绿色线是最短路,如果我们按照蓝色的区域去划分的话
不如把黄色部分也划进来,这样答案不会更劣
接着,我们把每个点按顺序拆成 \(4\) 个点 \(0,1,2,3\) ,每个点向顺时针的下一个点连边权为 \(0\) 的边
两个跨过一条边的点要连边权为权值的边
那么任何一个可以自交的环可以看做从左上角的 \(1\) 到左上角的 \(3\) 的一条路径
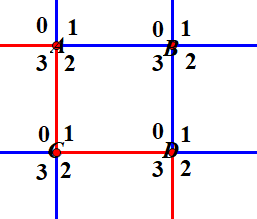
图中红色部分代表最短路,由于我们答案路径要包含最短路所以\((A 0 , A 3 ), (A 2 , A 3 ), (C 0 , C 1 ), (C 1 , C 2 ), (D 0 , D 3 ), (D 2 , D 3 )\)之间不能连边
当然这还不够,我们还需要保证我们的路径能够把所有的关键点包起来
这就相当于是我们的路径不能经过关键点里面的 \(4\) 个点,在连边时去掉这些点即可
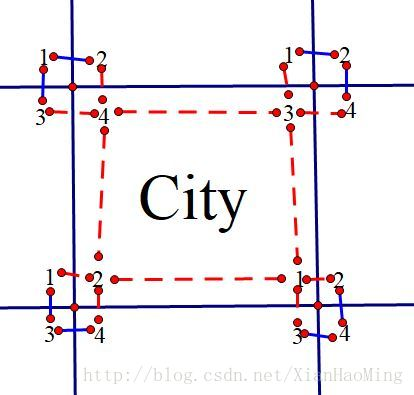
就是图中红色虚线的部分
注意左上角的 \((0,1),(0,3)\)不能连边
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<queue>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<‘0‘ || ch>‘9‘){
if(ch==‘-‘) fh=-1;
ch=getchar();
}
while(ch>=‘0‘ && ch<=‘9‘){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=3e6+5,maxm=405;
int val1[maxm][maxm],val2[maxm][maxm],a[maxm][maxm],rk[maxm][maxm],n,m,cnt,rkx[maxn],rky[maxn],jud[maxn];
int getid(rg int i,rg int j,rg int id){
return id*(n+1)*(m+1)+(i-1)*(m+1)+j;
}
int h[maxn],tot=1;
struct asd{
int from,to,nxt,val;
}b[maxn];
void ad(rg int aa,rg int bb,rg int cc){
b[tot].from=aa;
b[tot].to=bb;
b[tot].nxt=h[aa];
b[tot].val=cc;
h[aa]=tot++;
}
struct jie{
int num;
long long jl;
jie(){}
jie(rg int aa,rg long long bb){
num=aa,jl=bb;
}
bool operator < (const jie& A)const{
return jl>A.jl;
}
};
std::priority_queue<jie> q;
int vis[maxn],pre[maxn];
long long dis[maxn];
void dij(rg int qd){
memset(dis,0x3f,sizeof(dis));
memset(pre,0,sizeof(pre));
memset(vis,0,sizeof(vis));
dis[qd]=0;
q.push(jie(qd,dis[qd]));
while(!q.empty()){
rg int now=q.top().num;
q.pop();
if(vis[now]) continue;
vis[now]=1;
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(dis[u]>dis[now]+b[i].val){
dis[u]=dis[now]+b[i].val;
pre[u]=i;
q.push(jie(u,dis[u]));
}
}
}
}
bool ban[maxn][4];
void updat(rg int now){
while(now){
jud[pre[now]]=1;
now=b[pre[now]].from;
}
}
void gettag(rg int aa,rg int bb){
if(rkx[aa]==rkx[bb]){
if(rky[aa]>rky[bb]) std::swap(aa,bb);
ban[aa][1]=ban[bb][3]=1;
} else {
if(rkx[aa]>rkx[bb]) std::swap(aa,bb);
ban[aa][2]=ban[bb][0]=1;
}
}
int main(){
memset(h,-1,sizeof(h));
n=read(),m=read();
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
a[i][j]=read();
}
}
for(rg int i=1;i<=n+1;i++){
for(rg int j=1;j<=m+1;j++){
rk[i][j]=++cnt;
rkx[cnt]=i,rky[cnt]=j;
}
}
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m+1;j++){
val1[i][j]=read();
ad(rk[i][j],rk[i+1][j],val1[i][j]),ad(rk[i+1][j],rk[i][j],val1[i][j]);
}
}
for(rg int i=1;i<=n+1;i++){
for(rg int j=1;j<=m;j++){
val2[i][j]=read();
ad(rk[i][j],rk[i][j+1],val2[i][j]),ad(rk[i][j+1],rk[i][j],val2[i][j]);
}
}
dij(rk[1][1]);
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m;j++){
if(a[i][j]){
updat(rk[i][j]);
ban[rk[i][j]][1]=ban[rk[i][j]][2]=1;
ban[rk[i][j+1]][2]=ban[rk[i][j+1]][3]=1;
ban[rk[i+1][j]][0]=ban[rk[i+1][j]][1]=1;
ban[rk[i+1][j+1]][0]=ban[rk[i+1][j+1]][3]=1;
}
}
}
for(rg int i=1;i<tot;i++){
if(jud[i]) gettag(b[i].from,b[i].to);
}
tot=1;
memset(h,-1,sizeof(h));
ban[rk[1][1]][0]=ban[rk[1][1]][3]=1;
for(rg int i=1;i<=n+1;i++){
for(rg int j=1;j<=m+1;j++){
if(!ban[rk[i][j]][0]) ad(getid(i,j,0),getid(i,j,1),0),ad(getid(i,j,1),getid(i,j,0),0);
if(!ban[rk[i][j]][1]) ad(getid(i,j,1),getid(i,j,2),0),ad(getid(i,j,2),getid(i,j,1),0);
if(!ban[rk[i][j]][2]) ad(getid(i,j,2),getid(i,j,3),0),ad(getid(i,j,3),getid(i,j,2),0);
if(!ban[rk[i][j]][3]) ad(getid(i,j,3),getid(i,j,0),0),ad(getid(i,j,0),getid(i,j,3),0);
}
}
for(rg int i=1;i<=n;i++){
for(rg int j=1;j<=m+1;j++){
ad(getid(i,j,3),getid(i+1,j,0),val1[i][j]),ad(getid(i+1,j,0),getid(i,j,3),val1[i][j]);
ad(getid(i,j,2),getid(i+1,j,1),val1[i][j]),ad(getid(i+1,j,1),getid(i,j,2),val1[i][j]);
}
}
for(rg int i=1;i<=n+1;i++){
for(rg int j=1;j<=m;j++){
ad(getid(i,j,1),getid(i,j+1,0),val2[i][j]),ad(getid(i,j+1,0),getid(i,j,1),val2[i][j]);
ad(getid(i,j,2),getid(i,j+1,3),val2[i][j]),ad(getid(i,j+1,3),getid(i,j,2),val2[i][j]);
}
}
dij(getid(1,1,1));
printf("%lld\n",dis[getid(1,1,3)]);
return 0;
}
原文:https://www.cnblogs.com/liuchanglc/p/14358828.html