欧拉函数

欧拉函数公式

试除法求欧拉函数

#include <iostream>

using namespace std;

int main()
{
    int n;
    cin >> n;
    while (n --)
    {
        int x;
        cin >> x;
        
        int res = x;
        for (int i = 2; i <= x / i; ++ i)
            if (x % i == 0)
            {
                res -= res / i;
                while (x % i == 0) x /= i;
            }
        if (x > 1) res -= res / x;
        
        cout << res << endl;
    }
}

筛法求欧拉函数

在一些情况，需要求出1到n所有数的欧拉函数，如果对每个数都使用试除法求一遍太慢了。而筛法求欧拉函数就可以用于这类问题

算法原理

下面的代码是欧拉筛的代码，在欧拉筛质数的过程中，可以顺带着求出所有数的欧拉函数值

void get_divisors(int n)
{
    for (int i = 2; i <= n; ++ i)
    {
        if (!st[i]) primes[cnt ++] = i;
        for (int j = 0; primes[j] <= n / i; ++ j)
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

1. 如果判定某个数p为质数，则可直接得出其欧拉函数值为p-1

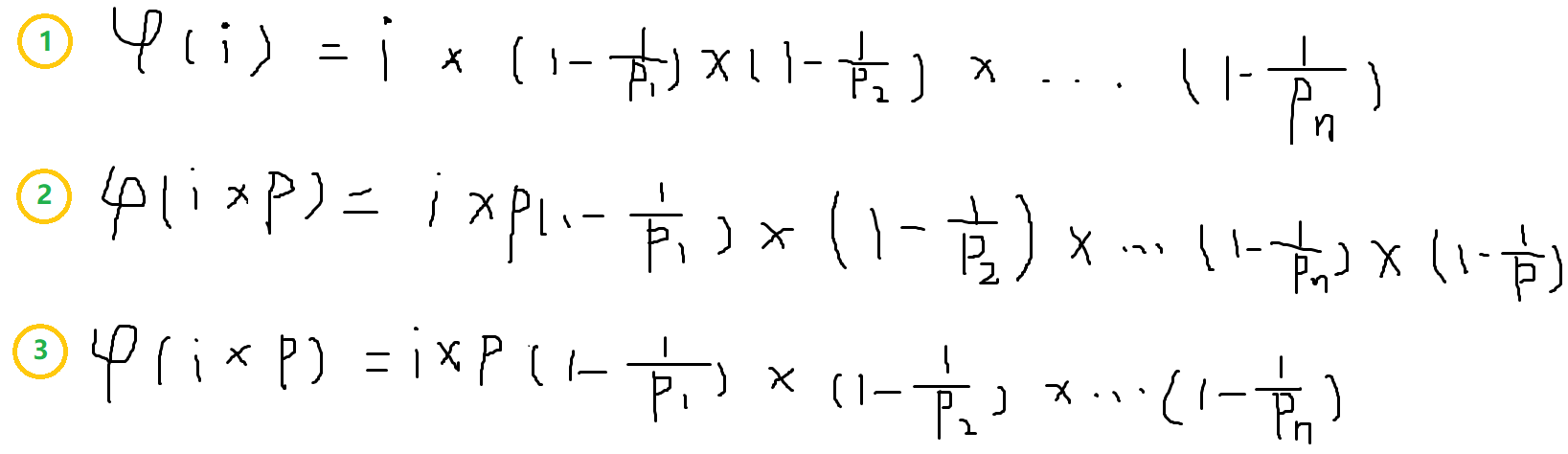
图中的p表示一个质数，和代码中的primes[j]是一样的
2. 如果 i % primes[j] == 0，说明primes[j]是i的最小质因子，即i的质因数中包含primes[j]，所以primes[j]对于i的质因数分解的影响只是增加了其中某个质数的指数，并没有增加质因数的种类，所以对于计算欧拉函数的影响只不过是在i的欧拉函数值基础上乘以一个primes[j]即可(对应着3式)
3.如果i % primes[j] != 0，说明 primes[j]不是i的质因子，primes[j]对于i的质因数分解的影响是增加了一个质数，这是种类增多了，所以在计算欧拉函数时就需要多乘以一个(1-1/p)和primes[j]，(对应着2式)

正确性说明

之前我们说明过枚举到i时，一定可以确定i是合数还是素数了，同理，也一定已经获得了i的欧拉函数值，所以才可以通过i和primes[j]的欧拉函数确定i * primes[j]的欧拉函数

代码实现

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int primes[N], cnt;
int phi[N];
bool st[N];

void get_divisors(int n)
{
    phi[1] = 1;
    for (int i = 2; i <= n; ++ i)
    {
        if (!st[i])
        {
            phi[i] = i - 1;
            primes[cnt ++] = i;
        }
        for (int j = 0; primes[j] <= n / i; ++ j)
        {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0)
            {
                phi[i * primes[j]] = phi[i] * primes[j]; // 对应3式
                break;
            }
            phi[i * primes[j]] = phi[i] * (primes[j] - 1); // 对应2式，只不过把primes[j]*(1 - 1 / primes[j])乘进去了
        }
    }
}
int main()
{
    int n;
    cin >> n;
    get_divisors(n);
    
    long long res = 0;
    for (int i = 1; i <= n; ++ i) res += phi[i];
    cout << res << endl;
    
    return 0;
    
}

欧拉函数

原文：https://www.cnblogs.com/G-H-Y/p/14361287.html