题1:如下图,以EF为直径的半圆与长方形ABCD的每条边恰有一个交点。EF=20,FC=2。求阴影部分的面积。
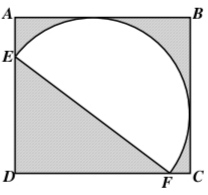
分析:只要求出长方形的长和宽就好。
解:按下图添加辅助线
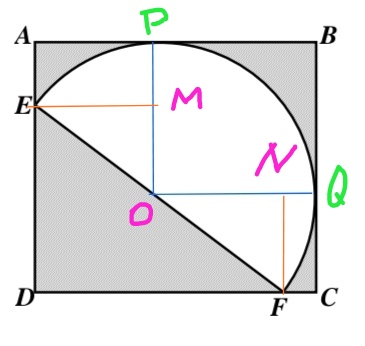
易知EM=ON=OQ-NQ=20/2-2=8,于是得到长方形的长为EM+OQ=8+10=18。
FN*FN=OF*OF-ON*ON=100-64=36,故FN=6,于是得到长方形的宽为6+10=16。
所求阴影部分的面积为
16*18-50pi。
题2:如下图,点O为正三角形ABC的中心,点M在AB上,点N在AC上,连接MN,交OB和OC分别于点P和点Q。已知MP=PQ=QN,AM=2BM,三角形OPQ的面积为1。求三角形ABC的面积。
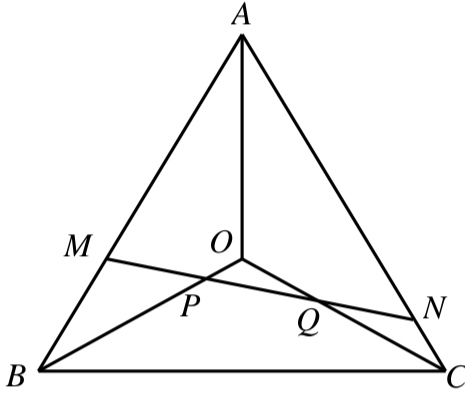
分析:本题的信息比较多,既有正三角形本身的特性,又有另外给出的线段比例关系。如何充分利用这些信息是解题的关键。
解:连接MO并延长交AC于点E,过点N作ME的平行线分别交AB和OB于点F和点H,如下图所示:
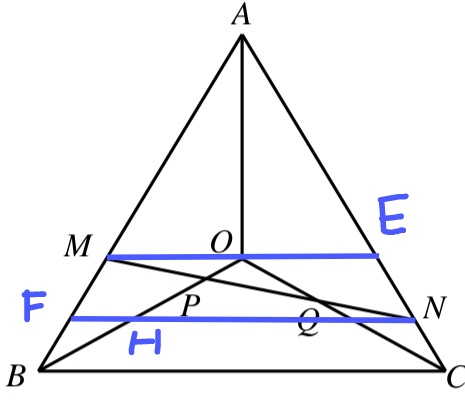
由AM=2BM以及正三角形的特性,可知ME//BC。
考察三角形MOP和NHP,由题设知PN=2PM,从而可知HN=2MO=ME,即MENH为平行四边形,进而易知MFH为正三角形,另外由正三角形特性易知FB=FH,于是MF=FB,即FN到上下两条平行线是等距的。
设MO为b,点P到MO的距离为h,由题设知三角形MOP的面积为bh/2=1,即bh=2。
由前述的三角形MOP和NHP的关系易知,ME到FN的距离为h+2h=3h,于是正三角形ABC的高为3h*6=18h。而AB=3BM=3MO=3b,于是三角形ABC的面积为3b*18h/2=3*18*2/2=54。
原文:https://www.cnblogs.com/readalps/p/14361380.html