作者:elfin
from sklearn.datasets import load_boston
dataset = load_boston()
dir(dataset)
---------------------------------------------------------------
out[1]:
[‘DESCR‘, ‘data‘, ‘feature_names‘, ‘filename‘, ‘target‘]
print(dataset["DESCR"])
.. _boston_dataset:
Boston house prices dataset
“---------------------------”
**Data Set Characteristics:**
:Number of Instances: 506
:Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.
:Attribute Information (in order):
- CRIM per capita crime rate by town
- ZN proportion of residential land zoned for lots over 25,000 sq.ft.
- INDUS proportion of non-retail business acres per town
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX nitric oxides concentration (parts per 10 million)
- RM average number of rooms per dwelling
- AGE proportion of owner-occupied units built prior to 1940
- DIS weighted distances to five Boston employment centres
- RAD index of accessibility to radial highways
- TAX full-value property-tax rate per $10,000
- PTRATIO pupil-teacher ratio by town
- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
- LSTAT % lower status of the population
- MEDV Median value of owner-occupied homes in $1000‘s
:Missing Attribute Values: None
:Creator: Harrison, D. and Rubinfeld, D.L.
This is a copy of UCI ML housing dataset.
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/
This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
The Boston house-price data of Harrison, D. and Rubinfeld, D.L. ‘Hedonic
prices and the demand for clean air‘, J. Environ. Economics & Management,
vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, ‘Regression diagnostics
...‘, Wiley, 1980. N.B. Various transformations are used in the table on
pages 244-261 of the latter.
The Boston house-price data has been used in many machine learning papers that address regression
problems.
.. topic:: References
- Belsley, Kuh & Welsch, ‘Regression diagnostics: Identifying Influential Data and Sources of Collinearity‘, Wiley, 1980. 244-261.
- Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.print(dataset["feature_names"])
---------------------------------------------------------------
out[2]:
array([‘CRIM‘, ‘ZN‘, ‘INDUS‘, ‘CHAS‘, ‘NOX‘, ‘RM‘, ‘AGE‘, ‘DIS‘, ‘RAD‘,
‘TAX‘, ‘PTRATIO‘, ‘B‘, ‘LSTAT‘], dtype=‘<U7‘)
在描述中,我们可以知道,其特征说明是按照顺序的,“RM”对应的index为5。
print(dataset["data"][:, 5])
array([6.575, 6.421, 7.185, 6.998, 7.147, 6.43 , 6.012, 6.172, 5.631,
6.004, 6.377, 6.009, 5.889, 5.949, 6.096, 5.834, 5.935, 5.99 ,
5.456, 5.727, 5.57 , 5.965, 6.142, 5.813, 5.924, 5.599, 5.813,
6.047, 6.495, 6.674, 5.713, 6.072, 5.95 , 5.701, 6.096, 5.933,
5.841, 5.85 , 5.966, 6.595, 7.024, 6.77 , 6.169, 6.211, 6.069,
5.682, 5.786, 6.03 , 5.399, 5.602, 5.963, 6.115, 6.511, 5.998,
5.888, 7.249, 6.383, 6.816, 6.145, 5.927, 5.741, 5.966, 6.456,
6.762, 7.104, 6.29 , 5.787, 5.878, 5.594, 5.885, 6.417, 5.961,
6.065, 6.245, 6.273, 6.286, 6.279, 6.14 , 6.232, 5.874, 6.727,
6.619, 6.302, 6.167, 6.389, 6.63 , 6.015, 6.121, 7.007, 7.079,
6.417, 6.405, 6.442, 6.211, 6.249, 6.625, 6.163, 8.069, 7.82 ,
7.416, 6.727, 6.781, 6.405, 6.137, 6.167, 5.851, 5.836, 6.127,
6.474, 6.229, 6.195, 6.715, 5.913, 6.092, 6.254, 5.928, 6.176,
6.021, 5.872, 5.731, 5.87 , 6.004, 5.961, 5.856, 5.879, 5.986,
5.613, 5.693, 6.431, 5.637, 6.458, 6.326, 6.372, 5.822, 5.757,
6.335, 5.942, 6.454, 5.857, 6.151, 6.174, 5.019, 5.403, 5.468,
4.903, 6.13 , 5.628, 4.926, 5.186, 5.597, 6.122, 5.404, 5.012,
5.709, 6.129, 6.152, 5.272, 6.943, 6.066, 6.51 , 6.25 , 7.489,
7.802, 8.375, 5.854, 6.101, 7.929, 5.877, 6.319, 6.402, 5.875,
5.88 , 5.572, 6.416, 5.859, 6.546, 6.02 , 6.315, 6.86 , 6.98 ,
7.765, 6.144, 7.155, 6.563, 5.604, 6.153, 7.831, 6.782, 6.556,
7.185, 6.951, 6.739, 7.178, 6.8 , 6.604, 7.875, 7.287, 7.107,
7.274, 6.975, 7.135, 6.162, 7.61 , 7.853, 8.034, 5.891, 6.326,
5.783, 6.064, 5.344, 5.96 , 5.404, 5.807, 6.375, 5.412, 6.182,
5.888, 6.642, 5.951, 6.373, 6.951, 6.164, 6.879, 6.618, 8.266,
8.725, 8.04 , 7.163, 7.686, 6.552, 5.981, 7.412, 8.337, 8.247,
6.726, 6.086, 6.631, 7.358, 6.481, 6.606, 6.897, 6.095, 6.358,
6.393, 5.593, 5.605, 6.108, 6.226, 6.433, 6.718, 6.487, 6.438,
6.957, 8.259, 6.108, 5.876, 7.454, 8.704, 7.333, 6.842, 7.203,
7.52 , 8.398, 7.327, 7.206, 5.56 , 7.014, 8.297, 7.47 , 5.92 ,
5.856, 6.24 , 6.538, 7.691, 6.758, 6.854, 7.267, 6.826, 6.482,
6.812, 7.82 , 6.968, 7.645, 7.923, 7.088, 6.453, 6.23 , 6.209,
6.315, 6.565, 6.861, 7.148, 6.63 , 6.127, 6.009, 6.678, 6.549,
5.79 , 6.345, 7.041, 6.871, 6.59 , 6.495, 6.982, 7.236, 6.616,
7.42 , 6.849, 6.635, 5.972, 4.973, 6.122, 6.023, 6.266, 6.567,
5.705, 5.914, 5.782, 6.382, 6.113, 6.426, 6.376, 6.041, 5.708,
6.415, 6.431, 6.312, 6.083, 5.868, 6.333, 6.144, 5.706, 6.031,
6.316, 6.31 , 6.037, 5.869, 5.895, 6.059, 5.985, 5.968, 7.241,
6.54 , 6.696, 6.874, 6.014, 5.898, 6.516, 6.635, 6.939, 6.49 ,
6.579, 5.884, 6.728, 5.663, 5.936, 6.212, 6.395, 6.127, 6.112,
6.398, 6.251, 5.362, 5.803, 8.78 , 3.561, 4.963, 3.863, 4.97 ,
6.683, 7.016, 6.216, 5.875, 4.906, 4.138, 7.313, 6.649, 6.794,
6.38 , 6.223, 6.968, 6.545, 5.536, 5.52 , 4.368, 5.277, 4.652,
5. , 4.88 , 5.39 , 5.713, 6.051, 5.036, 6.193, 5.887, 6.471,
6.405, 5.747, 5.453, 5.852, 5.987, 6.343, 6.404, 5.349, 5.531,
5.683, 4.138, 5.608, 5.617, 6.852, 5.757, 6.657, 4.628, 5.155,
4.519, 6.434, 6.782, 5.304, 5.957, 6.824, 6.411, 6.006, 5.648,
6.103, 5.565, 5.896, 5.837, 6.202, 6.193, 6.38 , 6.348, 6.833,
6.425, 6.436, 6.208, 6.629, 6.461, 6.152, 5.935, 5.627, 5.818,
6.406, 6.219, 6.485, 5.854, 6.459, 6.341, 6.251, 6.185, 6.417,
6.749, 6.655, 6.297, 7.393, 6.728, 6.525, 5.976, 5.936, 6.301,
6.081, 6.701, 6.376, 6.317, 6.513, 6.209, 5.759, 5.952, 6.003,
5.926, 5.713, 6.167, 6.229, 6.437, 6.98 , 5.427, 6.162, 6.484,
5.304, 6.185, 6.229, 6.242, 6.75 , 7.061, 5.762, 5.871, 6.312,
6.114, 5.905, 5.454, 5.414, 5.093, 5.983, 5.983, 5.707, 5.926,
5.67 , 5.39 , 5.794, 6.019, 5.569, 6.027, 6.593, 6.12 , 6.976,
6.794, 6.03 ])这一章,我们主要使用各种方法预测房价!
首先将数据转换为我们常使用的格式,这里先使用DataFrame进行多维数组的计算。
import pandas as pd
import numpy as np
dataframe = pd.DataFrame(dataset["data"])
dataframe.columns = dataset["feature_names"]
dataframe["price"] = dataset["target"]
数据展示:
print(dataframe)
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT price
0 0.00632 18.0 2.31 0.0 0.538 6.575 65.2 4.0900 1.0 296.0 15.3 396.90 4.98 24.0
1 0.02731 0.0 7.07 0.0 0.469 6.421 78.9 4.9671 2.0 242.0 17.8 396.90 9.14 21.6
2 0.02729 0.0 7.07 0.0 0.469 7.185 61.1 4.9671 2.0 242.0 17.8 392.83 4.03 34.7
3 0.03237 0.0 2.18 0.0 0.458 6.998 45.8 6.0622 3.0 222.0 18.7 394.63 2.94 33.4
4 0.06905 0.0 2.18 0.0 0.458 7.147 54.2 6.0622 3.0 222.0 18.7 396.90 5.33 36.2
... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
501 0.06263 0.0 11.93 0.0 0.573 6.593 69.1 2.4786 1.0 273.0 21.0 391.99 9.67 22.4
502 0.04527 0.0 11.93 0.0 0.573 6.120 76.7 2.2875 1.0 273.0 21.0 396.90 9.08 20.6
503 0.06076 0.0 11.93 0.0 0.573 6.976 91.0 2.1675 1.0 273.0 21.0 396.90 5.64 23.9
504 0.10959 0.0 11.93 0.0 0.573 6.794 89.3 2.3889 1.0 273.0 21.0 393.45 6.48 22.0
505 0.04741 0.0 11.93 0.0 0.573 6.030 80.8 2.5050 1.0 273.0 21.0 396.90 7.88 11.9
506 rows × 14 columns计算特征间的相关系数:
print(dataframe.corr())
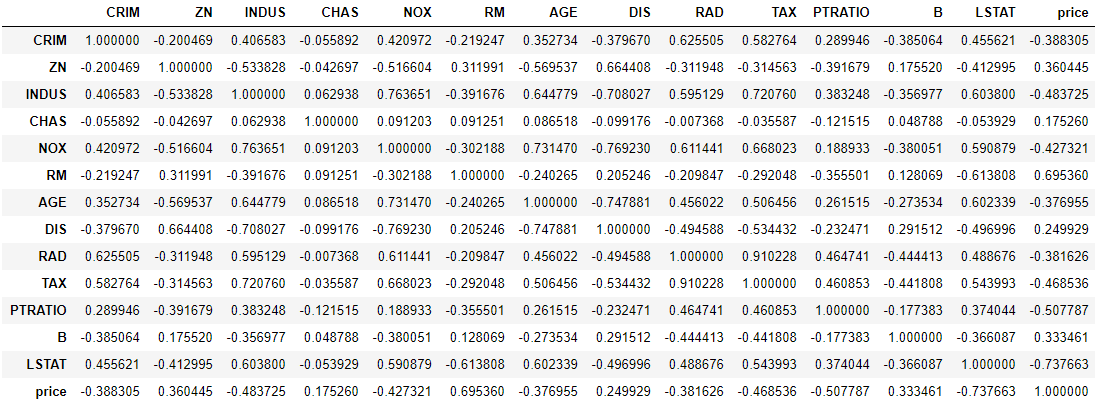
输出相关系数的热力图:
import seaborn as sns
print(sns.heatmap(dataframe.corr(), annot=True, fmt=".1f"))
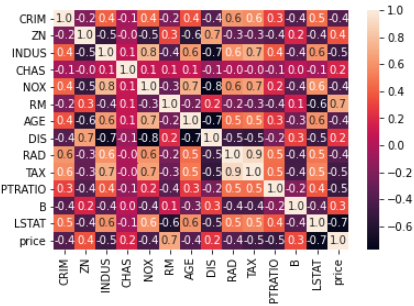
最初,人类可以根据已有的数据对新的数据进行预测,预测是基于原始数据的一一映射。
创建数据字典:
x_rm = dataframe["RM"].values
y_rm = dataframe["price"].values
rm_to_price = {r:y for r, y in zip(x_rm, y_rm)}
查看数据字典:
print(rm_to_price)
{6.575: 24.0,
6.421: 21.6,
7.185: 34.9,
6.998: 33.4,
7.147: 36.2,
6.43 : 28.7,
6.012: 22.9,
6.172: 27.1,
5.631: 16.5,
6.004: 20.3,
6.377: 15.0,
6.009: 21.7,
5.889: 21.7,
5.949: 20.4,
6.096: 13.5,
5.834: 19.9,
5.935: 8.4,
5.99 : 17.5,
5.456: 20.2,
5.727: 18.2,
5.57 : 13.6,
5.965: 19.6,
6.142: 15.2,
5.813: 16.6,
5.924: 15.6,
5.599: 13.9,
6.047: 14.8,
6.495: 26.4,
6.674: 21.0,
5.713: 20.1,
6.072: 14.5,
5.95 : 13.2,
5.701: 13.1,
5.933: 18.9,
5.841: 20.0,
5.85 : 21.0,
5.966: 16.0,
6.595: 30.8,
7.024: 34.9,
6.77 : 26.6,
6.169: 25.3,
6.211: 25.0,
6.069: 21.2,
5.682: 19.3,
5.786: 20.0,
6.03 : 11.9,
5.399: 14.4,
5.602: 19.4,
5.963: 19.7,
6.115: 20.5,
6.511: 25.0,
5.998: 23.4,
5.888: 23.3,
7.249: 35.4,
6.383: 24.7,
6.816: 31.6,
6.145: 23.3,
5.927: 19.6,
5.741: 18.7,
6.456: 22.2,
6.762: 25.0,
7.104: 33.0,
6.29 : 23.5,
5.787: 19.4,
5.878: 22.0,
5.594: 17.4,
5.885: 20.9,
6.417: 13.0,
5.961: 20.5,
6.065: 22.8,
6.245: 23.4,
6.273: 24.1,
6.286: 21.4,
6.279: 20.0,
6.14 : 20.8,
6.232: 21.2,
5.874: 20.3,
6.727: 27.5,
6.619: 23.9,
6.302: 24.8,
6.167: 19.9,
6.389: 23.9,
6.63 : 27.9,
6.015: 22.5,
6.121: 22.2,
7.007: 23.6,
7.079: 28.7,
6.405: 12.5,
6.442: 22.9,
6.249: 20.6,
6.625: 28.4,
6.163: 21.4,
8.069: 38.7,
7.82 : 45.4,
7.416: 33.2,
6.781: 26.5,
6.137: 19.3,
5.851: 19.5,
5.836: 19.5,
6.127: 22.7,
6.474: 19.8,
6.229: 21.4,
6.195: 21.7,
6.715: 22.8,
5.913: 18.8,
6.092: 18.7,
6.254: 18.5,
5.928: 18.3,
6.176: 21.2,
6.021: 19.2,
5.872: 20.4,
5.731: 19.3,
5.87 : 22.0,
5.856: 21.1,
5.879: 18.8,
5.986: 21.4,
5.613: 15.7,
5.693: 16.2,
6.431: 24.6,
5.637: 14.3,
6.458: 19.2,
6.326: 24.4,
6.372: 23.0,
5.822: 18.4,
5.757: 15.0,
6.335: 18.1,
5.942: 17.4,
6.454: 17.1,
5.857: 13.3,
6.151: 17.8,
6.174: 14.0,
5.019: 14.4,
5.403: 13.4,
5.468: 15.6,
4.903: 11.8,
6.13 : 13.8,
5.628: 15.6,
4.926: 14.6,
5.186: 17.8,
5.597: 15.4,
6.122: 22.1,
5.404: 19.3,
5.012: 15.3,
5.709: 19.4,
6.129: 17.0,
6.152: 8.7,
5.272: 13.1,
6.943: 41.3,
6.066: 24.3,
6.51 : 23.3,
6.25 : 27.0,
7.489: 50.0,
7.802: 50.0,
8.375: 50.0,
5.854: 10.8,
6.101: 25.0,
7.929: 50.0,
5.877: 23.8,
6.319: 23.8,
6.402: 22.3,
5.875: 50.0,
5.88 : 19.1,
5.572: 23.1,
6.416: 23.6,
5.859: 22.6,
6.546: 29.4,
6.02 : 23.2,
6.315: 22.3,
6.86 : 29.9,
6.98 : 29.8,
7.765: 39.8,
6.144: 19.8,
7.155: 37.9,
6.563: 32.5,
5.604: 26.4,
6.153: 29.6,
7.831: 50.0,
6.782: 7.5,
6.556: 29.8,
6.951: 26.7,
6.739: 30.5,
7.178: 36.4,
6.8 : 31.1,
6.604: 29.1,
7.875: 50.0,
7.287: 33.3,
7.107: 30.3,
7.274: 34.6,
6.975: 34.9,
7.135: 32.9,
6.162: 13.3,
7.61 : 42.3,
7.853: 48.5,
8.034: 50.0,
5.891: 22.6,
5.783: 22.5,
6.064: 24.4,
5.344: 20.0,
5.96 : 21.7,
5.807: 22.4,
6.375: 28.1,
5.412: 23.7,
6.182: 25.0,
6.642: 28.7,
5.951: 21.5,
6.373: 23.0,
6.164: 21.7,
6.879: 27.5,
6.618: 30.1,
8.266: 44.8,
8.725: 50.0,
8.04 : 37.6,
7.163: 31.6,
7.686: 46.7,
6.552: 31.5,
5.981: 24.3,
7.412: 31.7,
8.337: 41.7,
8.247: 48.3,
6.726: 29.0,
6.086: 24.0,
6.631: 25.1,
7.358: 31.5,
6.481: 23.7,
6.606: 23.3,
6.897: 22.0,
6.095: 20.1,
6.358: 22.2,
6.393: 23.7,
5.593: 17.6,
5.605: 18.5,
6.108: 21.9,
6.226: 20.5,
6.433: 24.5,
6.718: 26.2,
6.487: 24.4,
6.438: 24.8,
6.957: 29.6,
8.259: 42.8,
5.876: 20.9,
7.454: 44.0,
8.704: 50.0,
7.333: 36.0,
6.842: 30.1,
7.203: 33.8,
7.52 : 43.1,
8.398: 48.8,
7.327: 31.0,
7.206: 36.5,
5.56 : 22.8,
7.014: 30.7,
8.297: 50.0,
7.47 : 43.5,
5.92 : 20.7,
6.24 : 25.2,
6.538: 24.4,
7.691: 35.2,
6.758: 32.4,
6.854: 32.0,
7.267: 33.2,
6.826: 33.1,
6.482: 29.1,
6.812: 35.1,
6.968: 10.4,
7.645: 46.0,
7.923: 50.0,
7.088: 32.2,
6.453: 22.0,
6.23 : 20.1,
6.209: 21.4,
6.565: 24.8,
6.861: 28.5,
7.148: 37.3,
6.678: 28.6,
6.549: 27.1,
5.79 : 20.3,
6.345: 22.5,
7.041: 29.0,
6.871: 24.8,
6.59 : 22.0,
6.982: 33.1,
7.236: 36.1,
6.616: 28.4,
7.42 : 33.4,
6.849: 28.2,
6.635: 24.5,
5.972: 20.3,
4.973: 16.1,
6.023: 19.4,
6.266: 21.6,
6.567: 23.8,
5.705: 16.2,
5.914: 17.8,
5.782: 19.8,
6.382: 23.1,
6.113: 21.0,
6.426: 23.8,
6.376: 17.7,
6.041: 20.4,
5.708: 18.5,
6.415: 25.0,
6.312: 21.2,
6.083: 22.2,
5.868: 19.3,
6.333: 22.6,
5.706: 17.1,
6.031: 19.4,
6.316: 22.2,
6.31 : 20.7,
6.037: 21.1,
5.869: 19.5,
5.895: 18.5,
6.059: 20.6,
5.985: 19.0,
5.968: 18.7,
7.241: 32.7,
6.54 : 16.5,
6.696: 23.9,
6.874: 31.2,
6.014: 17.5,
5.898: 17.2,
6.516: 23.1,
6.939: 26.6,
6.49 : 22.9,
6.579: 24.1,
5.884: 18.6,
6.728: 14.9,
5.663: 18.2,
5.936: 13.5,
6.212: 17.8,
6.395: 21.7,
6.112: 22.6,
6.398: 25.0,
6.251: 12.6,
5.362: 20.8,
5.803: 16.8,
8.78 : 21.9,
3.561: 27.5,
4.963: 21.9,
3.863: 23.1,
4.97 : 50.0,
6.683: 50.0,
7.016: 50.0,
6.216: 50.0,
4.906: 13.8,
4.138: 11.9,
7.313: 15.0,
6.649: 13.9,
6.794: 22.0,
6.38 : 9.5,
6.223: 10.2,
6.545: 10.9,
5.536: 11.3,
5.52 : 12.3,
4.368: 8.8,
5.277: 7.2,
4.652: 10.5,
5.0 : 7.4,
4.88: 10.2,
5.39: 19.7,
6.051: 23.2,
5.036: 9.7,
6.193: 11.0,
5.887: 12.7,
6.471: 13.1,
5.747: 8.5,
5.453: 5.0,
5.852: 6.3,
5.987: 5.6,
6.343: 7.2,
6.404: 12.1,
5.349: 8.3,
5.531: 8.5,
5.683: 5.0,
5.608: 27.9,
5.617: 17.2,
6.852: 27.5,
6.657: 17.2,
4.628: 17.9,
5.155: 16.3,
4.519: 7.0,
6.434: 7.2,
5.304: 12.0,
5.957: 8.8,
6.824: 8.4,
6.411: 16.7,
6.006: 14.2,
5.648: 20.8,
6.103: 13.4,
5.565: 11.7,
5.896: 8.3,
5.837: 10.2,
6.202: 10.9,
6.348: 14.5,
6.833: 14.1,
6.425: 16.1,
6.436: 14.3,
6.208: 11.7,
6.629: 13.4,
6.461: 9.6,
5.627: 12.8,
5.818: 10.5,
6.406: 17.1,
6.219: 18.4,
6.485: 15.4,
6.459: 11.8,
6.341: 14.9,
6.185: 14.6,
6.749: 13.4,
6.655: 15.2,
6.297: 16.1,
7.393: 17.8,
6.525: 14.1,
5.976: 12.7,
6.301: 14.9,
6.081: 20.0,
6.701: 16.4,
6.317: 19.5,
6.513: 20.2,
5.759: 19.9,
5.952: 19.0,
6.003: 19.1,
5.926: 24.5,
6.437: 23.2,
5.427: 13.8,
6.484: 16.7,
6.242: 23.0,
6.75 : 23.7,
7.061: 25.0,
5.762: 21.8,
5.871: 20.6,
6.114: 19.1,
5.905: 20.6,
5.454: 15.2,
5.414: 7.0,
5.093: 8.1,
5.983: 20.1,
5.707: 21.8,
5.67 : 23.1,
5.794: 18.3,
6.019: 21.2,
5.569: 17.5,
6.027: 16.8,
6.593: 22.4,
6.12 : 20.6,
6.976: 23.9}当前的方法对于没有历史数据的key就会失效,那么我们该怎么对未知数据进行估计呢?
KNN是非常经典的算法,你可以用作分类也可以用作回归,但是这里有一个问题:KNN的计算量非常大,预测时计算开销大,性能呢?
定义回归类型的KNN算法:
def KNN(history_price, query_x, topn=3):
most_similar_items = sorted(history_price.items(), key=lambda x_y: (x_y[0] - query_x)**2)[:topn]
most_similar_prices = [price for rm, price in most_similar_items]
return np.mean(most_similar_prices)
这里设置取最近的三个值取平均,即得到未知数据的预测,如:
print(KNN(rm_to_price, 4, topn=3))
--------------------------------------------------------------
out[3]:
14.6
这里我们使用KNN解决了从无到有的过程,关于性能嘛:只能说预测计算量大,但是换来的精度并不高,这里指预测结果的可靠度、损失等。
? 为什么要使用线性回归?不管数据的分布是什么样的,你总是可以假设其分布服从某个形如 \(y = k \times x + b\) 的形式。关于是否正确,实际上是非常重要的,不同的数据分布我们需要设定不同的分布函数,而常见的分布有很多,而那些我们无法直接写出其分布函数的怪异曲线更多。即使是一个著名分布函数的图像呈现在你面前,你很有可能只能识别其分布簇,而不知道其究竟是什么分布。
import matplotlib.pyplot as plt
plt.scatter(x_rm, y_rm)
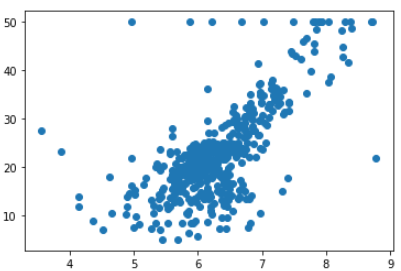
? 这里我们使用线性函数拟合?很明显其效果不会太好,因为离群点很多,数据分布没有明显的一次函数特性。但是我们现在只有小学3年级的水平,不知道更复杂的函数及其分布,就勉为其难使用 \(y_{\_rm} = k \times x_{\_rm} + b\) 进行拟合吧。
? 在拟合之前我们又要时刻了,我们该怎么拟合这些函数呢(参数 \(k\)、\(b\) 未知)?下面我们将使用不同的方法进行拟合。
? 要拟合这些函数,我们必须得知道哪个结构与真实分布更接近,即要有一个指标标识其模型的好坏!这里我们要介绍一个《近现代分析》中基础的评估指标MSE,即均方误差。它标识了在某个模型下,真实值与预测值之间平均的误差平方。
上面的公式展示了如何计算MSE。其中 \(\hat{y_{i}}\) 可以是线性函数也可以是非线性函数,这里我们是假设:\(\hat{y_{i}} = k \times x_{i} + b\) 。
定义MSE类型的损失函数:
def loss(y, yhat):
return np.mean((np.array(y) - np.array(yhat))**2)
若我们有数据如下:
y_real = [3,5, 9]
yhat1 = [3, 4,7]
yhat2 = [3,6,9]
则有:
print(loss(y_real, yhat1))
print(loss(y_real, yhat2))
------------------------------------------------------------------
out[4]:
1.6666666666666667
0.3333333333333333
上面的简单案例可以看出预测 yhat2 要好一些!
? 《近现代回归分析》中的第一章就指出我们求线性回归,可以使用最小二乘法。这里实际上是求:
这种方法实际上是我们常用的微积分方法,因为后面我们会进行求导,而对于多个参数,要求导函数为0对应的参数值,好像有点裂开,关于EM算法等等,有兴趣可以看一看。而在另一门课《高等数理统计》中,书中列举了各种各样的“随机模拟方法”,如大名鼎鼎的MCMC,这部分内容不难,但是也不好记,反正我以及还给老师(实际和分割求和取极限的思想一样;关于概率分布采样相当于从分布函数到自变量的求逆或者伪逆的过程;MCMC是蒙特卡洛+马尔科夫,细节自行百度)。
让计算机做参数拟合,这实际上是可能的,但是遇到的问题也挺复杂,考虑的点很多,上学的时候我们一般都在学习原理然后各种调包求值。我们常使用的软件有MATLAB、R、SAS。
下面我们来看最基础的随机模拟(和网格搜索有点类似,这种方法相当于在遍历所有可能性)。
import random
var_max, var_min = 20, -20
min_loss = float("INF")
total_times = 2000
def model(x, k, b):
return k * x + b
def magnitude(x):
"""获取迭代次数的数量级"""
if x < 10:
return 1
return magnitude(x / 10) + 1
%%time
def stochastic_simulation(total_times, var_max=20, var_min=-20):
min_loss = float("INF")
mt = magnitude(total_times)
for t in range(total_times):
k, b = random.randint(var_min, var_max), random.randint(var_min, var_max)
loss_ = loss(y_rm, model(x_rm, k, b))
if loss_ < min_loss:
min_loss = loss_
best_k, best_b = k, b
print(f"epoch:{t:0{mt}d}/{total_times}\t得到局部最优解 k={k}\tb={b} \tloss:{min_loss:.8g}")
return best_k, best_b
print(stochastic_simulation(total_times))
----------------------------------------------------------------------
out[5]:
epoch:0000/2000 得到局部最优解 k=-19 b=-18 loss:26013.775
epoch:0001/2000 得到局部最优解 k=12 b=16 loss:4792.5791
epoch:0003/2000 得到局部最优解 k=0 b=-13 loss:1346.9999
epoch:0005/2000 得到局部最优解 k=3 b=-17 loss:489.56346
epoch:0013/2000 得到局部最优解 k=0 b=20 loss:90.834664
epoch:0039/2000 得到局部最优解 k=3 b=6 loss:67.33391
epoch:0040/2000 得到局部最优解 k=4 b=0 loss:63.21599
epoch:0150/2000 得到局部最优解 k=5 b=-8 loss:52.684032
epoch:0446/2000 得到局部最优解 k=7 b=-20 loss:47.908237
Wall time: 46 ms
(7, -20)
? 这里我们迭代了2000个epoch,最终在第446次取到最优值 k=7 b=-20 loss:47.908237。经过分析可以发现这个方法的随机性非常大,损失下降也越来越慢,就如同学习越学越难,到最后一般都是学成了哲学。
注:代码是在jupyter notebook中运行的,所有使用%%time打印代码块运行时间。
? 在数值分析中,我们常常听说牛顿法等等,这些方法要解决的问题就是直接求解很难或者直接求不出的情况下,使用数值逼近的方法来近似,获得对真实分布的估计。梯度下降见名知义:梯度可以理解为一个向量,向量的每一个元素是函数对某个变量(我们这里是参数)的导数,对于某一个点,这些导数指向了函数“最陡峭”的方向,或者说函数值爬升最快的方向,其数值可以标识这种陡峭程度,绝对值越大,函数值变化越快。
? 我们这里要干什么?我们想让损失尽可能地小,即最小化 \(loss\)。对于给定一个点(一组参数),我们希望更新这组参数使得 \(loss\) 更小!直到取到最小损失对应的一组参数。对于这个给定的点即神经网络中的参数初始化。点可以初始化,该点的梯度也可以求出来,那我们怎么优化参数组呢?根据上一段的叙述,我们可以发现我们沿着梯度的反向走,损失就会变小。让参数沿着梯度的反方向更新即神经网络中的反向传播过程。
以线性回归为例,假设损失函数为:
关于参数的偏导数为:
参数k的偏导数
参数b的偏导数
参数的更新策略
定义偏导函数:
def partial_k(x, y, k_n, b_n):
return 2 * np.mean((k_n * x + b_n - y) * x)
def partial_b(x, y, k_n, b_n):
return 2 * np.mean(k_n * x + b_n - y)
初始化参数及超参数:
init_k_b = random.randint(var_min, var_max), random.randint(var_min, var_max)
# 使用梯度下降求解参数
min_loss = float("INF")
# 先随机初始化参数
k, b = init_k_b
# 初始化学习率
alpha = 1e-2
total_times = 2000
执行梯度下降算法:
%%time
mt = magnitude(total_times)
for t in range(total_times):
# 相对于神经网络里面的反向传播过程
k = k - partial_k(x_rm, y_rm, k, b) * alpha
b = b - partial_b(x_rm, y_rm, k, b) * alpha
# 参数更新后,计算新一轮的预测、误差
loss_ = loss(y_rm, model(x_rm, k, b))
if loss_ < min_loss:
min_loss = loss_
print(f"epoch:{t:0{mt}d}/{total_times}\t得到局部最优解 k={k}\tb={b} \tloss:{min_loss:.8g}")
--------------------------------------------------------------------------------
out[6]:
……
epoch:1995/2000 得到局部最优解 k=6.550545998853444 b=-18.43992351971027 loss:46.846278
epoch:1996/2000 得到局部最优解 k=6.551171643338578 b=-18.44390329457724 loss:46.844687
epoch:1997/2000 得到局部最优解 k=6.55179713441538 b=-18.447882093601475 loss:46.843096
epoch:1998/2000 得到局部最优解 k=6.5524224721214654 b=-18.451859917022254 loss:46.841506
epoch:1999/2000 得到局部最优解 k=6.553047656494441 b=-18.455836765078796 loss:46.839917
Wall time: 807 ms
? 这里的运行时间和损失都没有随机模拟好,这真是气死人!!!为什么会这样?
首先,我们把打印关了,因为打印是一个费时操作,随机模拟明显打印要少很多
关闭后两者的结果为:
随机模拟:
loss:47.908237
Wall time: 46 ms
梯度下降:
k=7.541206641502778 b=-24.74159550914088 loss:44.815201
Wall time: 95 ms
这里随机模拟还是要比梯度的计算速度快!不难发现梯度下降算法梯度一直在将,但是每次降低的损失很小,实际上这和学习率关系很大,假如梯度值是一个人的步幅,而某个是真实的步长是梯度乘以学习率,这里学习率都很小,所以给人的感觉是下降太慢。
梯度下降多次运行后稳定在k=9.101758320301588 b=-34.66839020811879 loss:43.600552。
多次运行随机模拟后,损失一般没有低于47!当然这不能说明谁比谁好,只能说梯度详解迭代足够多,有更高的可能性获得一个较好的一组参数。
经过对比发现梯度详解的结果不太稳定,实际上这和我们的初始化有关,这里才两个参数就有这么大的影响,如果是更高维的函数,我们的结果就更飘忽不定了,如何避免参数落入局部最优?这里会涉及优化方法的问题,后面再叙述。
%%time
update = True
for t in range(20000):
# 相对于神经网络里面的反向传播过程
gradient = [partial_k(x_rm, y_rm, k, b), partial_b(x_rm, y_rm, k, b)]
k = k - gradient[0] * alpha
b = b - gradient[1] * alpha
# 参数更新后,计算新一轮的预测、误差
loss_ = loss(y_rm, model(x_rm, k, b))
if loss_ < min_loss:
min_loss = loss_
best_k, best_b = k, b
# print(f"epoch:{t:0{mt}d}/{total_times}\t得到局部最优解 k={k}\tb={b} \tloss:{min_loss:.8g}")
# 更新学习率
if np.abs(loss_ - min_loss) < 0.001 and update:
alpha *= 0.5
update = False
print(f"k={k}\tb={b} \tloss:{min_loss:.8g}")
------------------------------------------------------------------------
out[7]:
k=9.04129745988521 b=-34.28379151313224 loss:43.602395
Wall time: 978 ms
? 最后计算得到loss:43.602395,这个好像还不如不更换学习率!!这里只能说模型的不确定性大于我们的优化策略,也即优化策略很垃圾!
from sklearn.linear_model import LinearRegression
slr = LinearRegression()
x_rm = x_rm.reshape(-1,1) # 处理成需要的数据格式
slr.fit(x_rm, y_rm)
y_hat = slr.predict(x_rm)
loss_lr = loss(y_rm, y_hat)
print(loss_lr)
-----------------------------------------------------------------------------
out[8]:
43.60055177116956
很明显别人的实现是比较稳定的,每次拟合都很好,且数值多次运行不会出现明显波动,即算法比较稳定!
误差分布:
plt.plot(y_hat - y_rm)
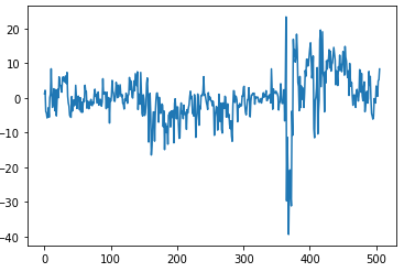
本文叙述了神经网络的主要过程:梯度更新、参数更新,下一章节将进一步说明!这里我们是从房价预测--->KNN--->线性回归--->MSE--->梯度下降!这个路径有助于我们思考神经网络的本质!
完!
原文:https://www.cnblogs.com/dan-baishucaizi/p/14362884.html