Codeforces Round 699 (Div.2) 题解

题目地址

F就咕咕了
A就不说了

B

直接模拟就好，因为\(n<=100\) 且\(h_i<=100\)巨石最多不会超过10000个，直接模拟放巨石过程就行

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 111;
int n, k, a[N];

void work()
{
	memset(a,0,sizeof(a));
	scanf("%lld%lld",&n,&k);
	for(int i = 1;i <= n; i++)
	    scanf("%lld",&a[i]);
	int sum = 0;
	a[0] = 101;
	for(;;)
	{		
     	int flag = 0; 
	//	output();
    	for(int i = 1;i <= n; i++)
    	{
	    	if(a[i] < a[i + 1])
		    {
			    flag = 1;
			    if(a[i - 1] >= a[i + 1]) 
			    {
			        int val = a[i + 1] - a[i];
			        a[i] += val;
				    sum += val; 
			    }
			    if(a[i - 1] < a[i + 1])
			    {
				    int val = a[i - 1] - a[i] + 1;
				    a[i] += val;
				    sum += val; 
			    }  
				if(sum >= k) { printf("%d\n",i); return; }
			    break;
  		    } 
        }
        if(!flag) break;
    }
	puts("-1");
} 

signed main()
{
	int t;scanf("%lld",&t);
	while(t --) work();
}

C

考虑构造
对于每一个\(i\)，如果\(a_i != b_i\)，那么我们需要找到一名画家，所图的颜色也为\(b_i\)，否则无解
先把\(a_i != b_i\)的情况解决掉，我们可以对每种颜色开个\(vector\)，对这样的i分配合适的画家
那么剩下的画家怎么办
其实我们只需要找到最后一名画家所画的位置即可
剩下未被分配的画家和第\(m\)个画家用相同的位置，这样对每个位置的颜色不会造成影响

using namespace std;
const int N = 2e5 + 101;
int a[N], b[N], c[N], ans[N];
vector<int>v[N];
int n, m;

void clear()
{
	for(int i = 1;i <= m; i++) ans[i] = 0;
	for(int i = 1;i <= n; i++)
	    v[i].clear();
}

void work()
{
	scanf("%d%d",&n,&m);
	clear();
	for(int i = 1;i <= n; i++) scanf("%d",&a[i]);
	for(int i = 1;i <= n; i++) scanf("%d",&b[i]);
	for(int i = 1;i <= m; i++) 
	    scanf("%d",&c[i]),v[c[i]].push_back(i);
	for(int i = 1;i <= n; i++)
	{
		if(a[i] != b[i]) 
		{
			if((int)v[b[i]].size() == 0) { puts("NO");return; }
			int painter = v[b[i]][(int)v[b[i]].size() - 1];
			v[b[i]].pop_back();
			ans[painter] = i;
		}
	}
	if(ans[m]) 
	{
		for(int i = m;i >= 1; i--)
		    if(!ans[i]) ans[i] = ans[m];
	}
	else
	{
		int flag = 0;
		for(int i = 1;i <= n; i++)
	    	if(c[m] == b[i]) ans[m] = i,flag = 1;
		if(!flag) { puts("NO"); return; }
		for(int i = m;i >= 1; i--)
		    if(!ans[i]) ans[i] = ans[m];
	}
	puts("YES");
	for(int i = 1;i <= m; i++)
	    printf("%d ",ans[i]);
	printf("\n");
}

signed main()
{
	int t;scanf("%d",&t);
	while(t --) work();
} 

D

同样是构造
我们知道题目所给的图是完全图
当\(m\)为奇数时，直接找两个点转圈就行
当\(m\)为偶数时，
如果\(n\)为2且\(a[1][2]!=a[2][1]\)那么问题显然无解
否则如果我们可以找到两个点满足\(a[i][j]==a[j][i]\)直接选择\(i\)和\(j\)转圈即可
剩下的情况就是\(n>=3\)且对于任意的\(i!=j\)有\(a[i][j]!=a[j][i]\)
通过画图可以发现
我们可以找到这样的三个点（其中i作为中间点）满足\(a[i][j]!=a[i][k]\)
这样就可以构造一种方案，

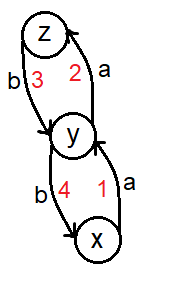
当\(m/2\)为偶数时，\(y->z->y->z ... ->y->x->y->...x->y\)
当\(m/2\)为奇数时，\(z->y->z->y ... ->y->x->y->...y->x\)
这样我们对所有的情况，找到对应的合适的方案
时间复杂度\(O(n^2)\)

#include <bits/stdc++.h>
using namespace std;

char a[1011][1011]; 
int n, m, ans[100551];

void work()
{
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= n; i++)
	    scanf("%s",a[i] + 1);
	if(m % 2 == 1)
	{
		puts("YES");
		for(int i = 1;i <= m + 1; i++)
		   printf("%d ",i % 2 == 0 ? 1 : 2);
		printf("\n");
		return;
	}
	if(m % 2 == 0)
	{
		if(n == 2 && a[1][2] != a[2][1]) puts("NO");
		else
		{
			for(int i = 1;i <= n; i++)
			for(int j = 1;j <= n; j++)
			{
				if(i == j) continue;
				if(a[i][j] == a[j][i])
				{
					puts("YES");
					for(int k = 1;k <= m + 1; k++)
					    printf("%d ",k % 2 == 0 ? i : j);
					printf("\n");
					return;
				}
			}
			for(int i = 1;i <= n; i++)
			for(int j = 1;j <= n; j++)
			for(int k = 1;k <= n; k++)
			{
				if(i == j || i == k || j == k) continue;
				if(a[i][j] != a[i][k])
				{			
				    puts("YES");
					ans[(m + 2) / 2] = i;
				    int pos = (m + 2) / 2;
				    ans[pos - 1] = j;
				    ans[pos + 1] = k;
				    for(int l = pos - 2;l >= 1; l--) ans[l] = ans[l + 2];
				    for(int l = pos + 2;l <= m + 1; l++) ans[l] = ans[l - 2];
				    for(int i = 1;i <= m + 1; i++)
				        printf("%d ",ans[i]);
				    printf("\n");
				    return;
				}
		    }
		} 
	}
}

signed main()
{
	int t;scanf("%d",&t);
	while(t --) work();
} 

/*
1
3 6
*aa
b*b
ba*
*/

E

DP就行（感觉有点抽象，可以手玩一下)
假设我们原来的序列为\(a_1a_2a_3...a_n\)
转换后序列没有操作的数就变为了\(a_{k_1},a_{k_2},a_{k_m}\)
\(k_1,k_2,...k_m\)是一个升序的\(1，2，3...n\)的子序列
操作的数就到达了序列的末尾
我们设\(dp[i]\)是到达i，符合题目条件子序列的最长的长度
设\(L[i]\)为i出现在原序列中最靠左的位置，\(R[i]\)为i出现在原序列最靠右的位置
不保留i则有\(dp[i]=max(dp[i],dp[i-1])\)
保留i则有\(dp[i]=max(dp[i],dp[L[a[i]]-1]+cnt[a[i]])\)当前仅当\(i==R[a[i]]\)
直接\(dp\)后我们发现dp[n]过不了第二个样例
通过手玩可以发现，当我们dp到i时，可以保留i后面的一些数与i前面操作的数拼成一段
最多可以保留的数\(ans=max(dp[i]+maxn)\)，其中maxn是i后面出现次数最多的数的出现次数
最后输出\(n-ans\)即可，时间复杂度\(O(n)\)

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 101;
int dp[N], a[N], n;
int L[N], R[N], cnt[N];

signed main()
{
	scanf("%d",&n);
	memset(L,127/3,sizeof(L));
	for(int i = 1;i <= n; i++) 
	{
		scanf("%d",&a[i]);
		L[a[i]] = min(L[a[i]],i);
		R[a[i]] = max(R[a[i]],i);
		cnt[a[i]] ++;
	}
	dp[0] = 0;
	for(int i = 1;i <= n; i++)
	{
		dp[i] = max(dp[i],dp[i - 1]);
		if(R[a[i]] == i)
			dp[i] = max(dp[i],dp[L[a[i]] - 1] + cnt[a[i]]);
	}
	memset(cnt,0,sizeof(cnt));
	int ans = 0, maxn = 0;
	for(int i = n;i >= 1; i--)
	{
		ans = max(ans,dp[i] + maxn);
		cnt[a[i]] ++;
		maxn = max(maxn,cnt[a[i]]); 
	}
	cout << n - ans;
}

F就咕咕了，有时间再更

Codeforces Round 699 (Div.2) 题解

原文：https://www.cnblogs.com/zjz2333/p/14381390.html