变分贝叶斯学习（variational bayesian learning）及重参数技巧（reparameterization trick）

摘要：常规的神经网络权重是一个确定的值，贝叶斯神经网络中，将权重视为一个概率分布。本文对贝叶斯神经网络的优化方法进行概述。

论文地址：http://proceedings.mlr.press/v37/blundell15.pdf

网络权重的点估计

常规神经网络可以基于MLE或MAP对权重作点估计。

基于MLE（maximum likelihood estimation）：

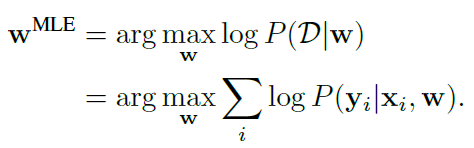
基于MAP（maximum a posteriori）：

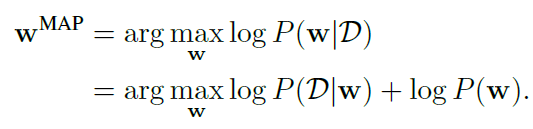
对权重施加先验，等价于进行正则化。如果施加的是高斯先验，相当于进行L2正则，如果是一个laplace先验，相当于L1正则。

 贝叶斯方法

贝叶斯推断在给定训练数据的情况下，计算网络参数的后验概率，理论上可以通过以下方式对样本标签所服从的分布进行预测：

 Hinton等人提出对网络权重的贝叶斯后验分布进行变分估计，变分学习寻找参数θ，来最小化分布q(w|θ）和权重真实后验分布之间的KL距离，这里的参数θ可理解为w所服从分布的参数，比如高斯的μ和σ：

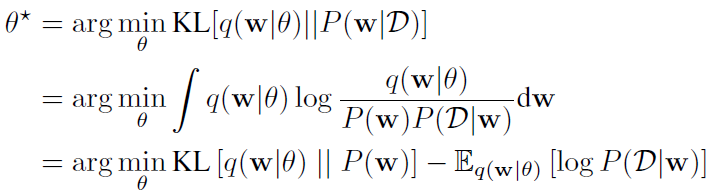
 这个loss函数就是变分自由能（variational free energy），也称为期望下界（expected lower bound， ELBO）。

可以将loss函数简记为：

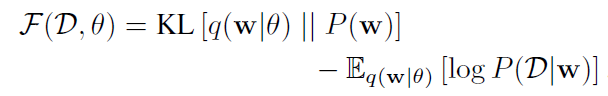损失函数的后半部分代表与数据相关，称之为似然损失，前半部分与先验有关，称为先验损失。该损失也被称为最小描述长度（minimum description length, MDL）

 无偏蒙特卡洛梯度

我们使用梯度下降的方式对上述损失进行优化。

在特定的条件下，期望的微分等于微分的期望。

命题1：假设ε服从分布q(ε)，令w = t(θ, ε)，其中t(θ, ε)是一个确定性函数，加入w的边缘密度q(w|θ)满足q(ε) dε = q(w|θ) dw，那么：

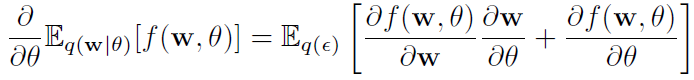
证明：

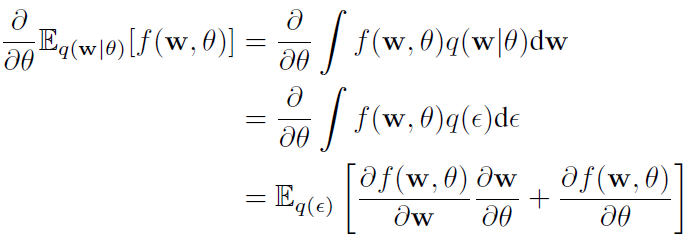
 确定性函数 t(θ, ε)将一个随机噪声和变分后验参数转换为一个变分后验。

令，我们可以将命题1用于优化。通过蒙特卡洛采样，可以通过反向传播算法对网络进行优化。

 命题1就是所谓的重参数技巧（reparameterization trick）。

变分高斯后验

基于高斯后验的变分学习训练过程如下：

这里就是常规反向传播算法得到的梯度。

变分贝叶斯学习（variational bayesian learning）及重参数技巧（reparameterization trick）

原文：https://www.cnblogs.com/zcsh/p/14386030.html