原文链接:https://blog.csdn.net/anhongning123/article/details/111033762
算法设计其实无非需要理解一下几点:
1.算法的目的是为了解决实际问题,应当为了更简便的解决实际问题设计算法(当然一些以安全为主的算法属于例外)
2.解决一个问题的方法并不唯一,但是总能通过“有效”的方法找到优秀的算法
3.优秀的算法往往代码也很简单
4.迭代式改进能够进一步改进算法
建议大家看看Algorithms原版(不要看汉化的,这是一本奇书),本文的内容就是书上的总结
假设问题的输入是一列元素对,其中每个元素都表示一个某种类型的对象,一对元素AB可以理解为“A与B具有连通性”。
相连性具有以下特点:

(1)6号与7号(6号图)
(2)4号与5号(12号图)
(3)8号与9号(11号图)
三对元素是符合连通的(或者称其为相连或者等价也可以),那么在输入处理时可以直接将以上三对元素忽略。
连通性的实用性很强,当然,学过数据结构的同学应该对这个定义很熟悉了。例如在处理网络(减少布线或者最短路径),引用(变量名称等价)等方面都具有较强实用性。
前言中的第一点——
算法的目的是为了解决实际问题,应当为了更简便的解决实际问题设计算法(当然一些以安全为主的算法属于例外)
对于连通性而言,讨论元素间是否连通,一般是为了求得所需连通元素之间的具体分量(也就是每一个分量的具体路径)
以下列出连通性与输出分量路径的关系
| 连通 | 不连通 | |
|---|---|---|
| 输出分量的具体路径(注意是否有向) | 1 | \ |
| 不输出分量的具体路径(注意是否有向) | 2 | 3 |
以上就是模型需要处理的问题(本文Union-Find算法仅解释第二种情况),当然,为了更好的对问题进行程序化表述,需要定义一组数据结构,
然后基于定义的数据结构完成分项的任务——
1. 定义数据结构(影响算法效率最直接的是数据结构)
2. 基于定义的数据结构完成分项操作
对于动态连通性的具体操作可以定义如下:
| 操作 | 解释 |
|---|---|
| 初始化 | 大多数算法在运行前都需要完成初始化操作 |
| 归并 | 完成两个独立的连通分量之间的连接 |
| 判断连接 | 判断两个元素是否属于同一连通分量 |
| 查找 | 找到需要的连通分量 |
| 计数 | 计算连通分量的数量 |
其实和数学建模的方法是一致的,设计算法都需要抽象量化。连通性的本质实际上就是带有连接方式的分组,在Union-Find算法中我们并不需要考虑连接方式的问题
因此可以有如下假设方式:
对于N个元素可以使用一个统一的id[]数组进行元素标记,如果两个元素连通,那么就可以修改其标记的数组为同一编号。在初始化时每个元素必然是不连通的,因此可以初始化id[i]=i
可以定义API如下:
| public class UnionFind | UnionFind | 初始化 |
|---|---|---|
| int find(int p) | 返回所在分量的标识 | |
| vioid union(int p,int q) | 连通两个元素 | |
| boolean connected(int p,int q) | 判断元素是否连通 | |
| int count() | 统计连通分量的数量 |
public class UnionFind
{
private int[] id; // 分量标识
private int count; // 分量数量
public UnionFind(int N)
{
// 初始化id数组
count = N;
id = new int[N];
for (int i = 0; i < N; i++)
id[i] = i;
}
public int count()
{ return count; }
public boolean connected(int p, int q)
{ return find(p) == find(q); }
public int find(int p);
public void union(int p, int q);
public static void main(string[] args)
{
//某输入输出操作
}
}
其实 Union-Find的具体设计就由
public int find(int p);
public void union(int p, int q);
两个函数确定,所以接下来主要探讨find和union的方法。
实现union其实就是改变每个分量的标识,那么最简单的思路就是判断两个元素的标号,如果不同就将其分量修改为相同的的标识
public class QuickFind
{
private int[] id; // 分量标识
private int count; // 分量数量
public QuickFind(int N)
{
// 初始化id数组
count = N;
id = new int[N];
for (int i = 0; i < N; i++)
id[i] = i;
}
public int count()
{ return count; }
public boolean connected(int p, int q)
{ return find(p) == find(q); }
public int find(int p)
{ return id[p]; }
public void union(int p, int q)
{
// 将p和q的归并为一组
int pID = find(p);
int qID = find(q);
// 元素已经连通则不做处理
if (pID == qID) return;
// 若不连通,直接改变标识
for (int i = 0; i < id.length; i++)
if (id[i] == pID) id[i] = qID;
count--;
}
public static void main(string[] args)
{
//某输入输出操作
}
}
以上代码可以使用下图阐述:
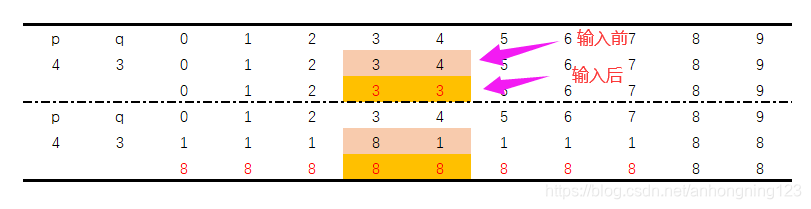
每次在输入后,都进行一次union遍历,如果元素处于不同分量,就将其修改为同一分量的标识,达到连通的效果。
Quick-Find的思路无疑是较为简便的,如果处理N个元素,意味着也要调用N-1次union,也就是说union的数量级是平方级别的。在数据规模较小的时候该算法会很简便,但如果数据规模较大,该算法显然不可行。
所以需要对以上算法进行优化,首先要明白调用union的次数是无法改变的,优化的目的就在
优化union上。
影响Quick-Find中union的因素是由于id[i]数组无法给出各个分量的具体元素类,如果想要得到 某一分量的全部元素只能遍历id[i].
因此为了提高效率,需要重新设计id[i]中元素的关系,也就是需要给出同一分量中各个元素的继承关系。
如下:

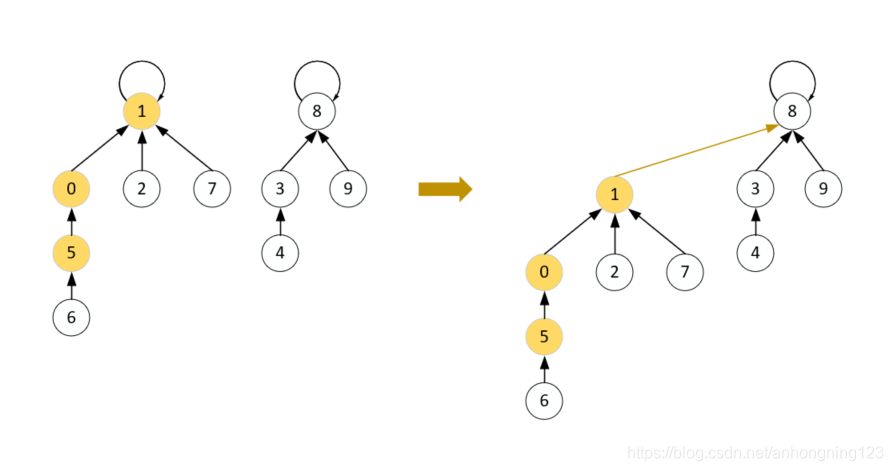
。
修改过程也会更为简单,只需将根节点指向另一根节点即可,如上图。
这里的id[]种存放的不再是元素,而是该元素的父节点,在遍历过程中总能找到一个根节点使得id[root]=root,于是可以用这个id[root]作为该分量的标识。并由此可以设计find函数。
实现代码如下:
private int find(int p)
{
//找到分量的代表元素
while (p != id[p]) p = id[p];
return p;
}
public void union(int p, int q)
{
// 使两节点的根节点统一
int pRoot = find(p);
int qRoot = find(q);
if (pRoot == qRoot)
return;
id[pRoot] = qRoot;
count--;
}
这里不建议使用链表或者图的结构,应为连id[]中需要使用一个标志性元素代表整个分量,在树中可以使用根节点作为唯一标识。而链表是线性结构,无法满足多对一的性质。
此外,对于增删改三种处理,效率最高的还是树。
Quick-Union 解决了union的遍历问题,但是在最坏的情况下,这种方式会退化成一个单链表。这种情况下也是平方级别的。
因为Quick-Union中的find是影响算法效率的主要原因,最坏情况下需要调用find的次数为3+5+7+9+......+(2N-1)
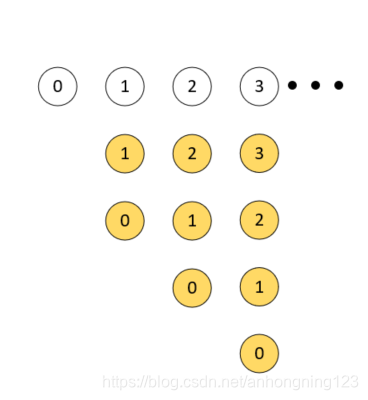
(尽管对于增删改三种处理,效率最高的还是树,但是树的结构会受到输入数据的结构影响)
这里给出路径压缩方式对Quick-Union的优化,对于Simpler one-pass variant优化的算法均摊成本为对数级别。
在Quick-Union中,实现find其实是向上遍历直到寻找到$root=id[root]$的节点,但在遍历过程中其实可以事先对遍历的路径进行优化。这里给出两种路径压缩的方法:

- 简化单通变体(路径减半)Simpler one-pass variant :使路径中的每一个其他节点指向它的爷爷节点,即$id[i] = id[id[i]]$;

// QuickUnionPathCompressionUF
//路径压缩算法主要优化的是find过程
public int find(int p) {
int root = p;
双通实现:添加第二个循环,将每个检查节点的id[]设置为根
while (root != id[root])
root = id[root];
while (p != root) {
int newp = id[p];
id[p] = root;
p = newp;
}
return root;
}
简化单通(路径减半):使路径中的每一个其他节点指向它的爷爷节点
public int find(int i){
while (i != id[i])
{
//如果p元素的父亲指针指向的不是自己,说明p并不是集合中的根元素,还需要一直向上查找和路径压缩
id[i] = id[id[i]];
i = id[i];
}
return i;
}
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
id[rootP] = rootQ;
count--;
}
显然,Quick-Union 算法 依旧存在着弊端,需要引入一种处理方法解决Quick-Union 算法的最坏情况,或者说使用一种方式让连通分量合并时find寻找根节点的路径更短,也就是让合并的后的分量高度更低。
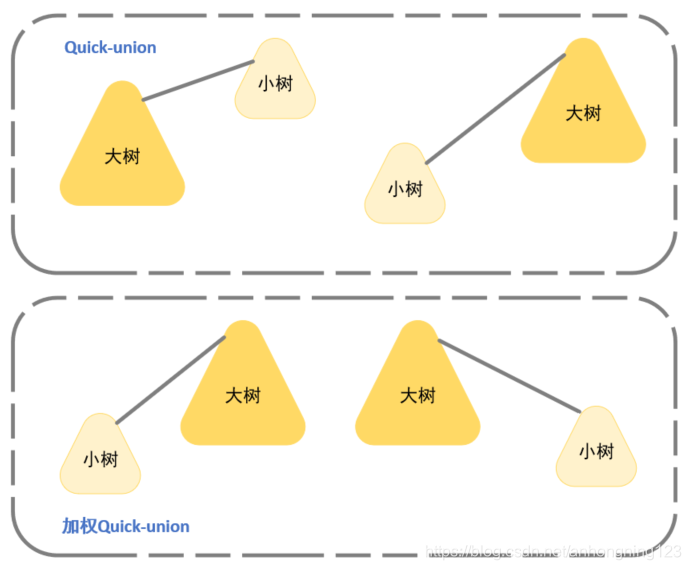
为此,需要设立一个数组存放根节点对应的分量大小。代码如下:
public class WeightedUnionFind
{
private int[] id; // 分量标识
private int[] sz; // 各个根节点所对应的根节点大小
private int count; // 分量数量
public WeightedUnionFind(int N)
{
// 初始化id数组
count = N;
id = new int[N];
for (int i = 0; i < N; i++)
id[i] = i;
// 初始化sz数组
sz = new int[N];
for (int i = 0; i < N; i++)
sz[i] = i;
}
public int count()
{ return count; }
public boolean connected(int p, int q)
{ return find(p) == find(q); }
private int find(int p)
{
//找到分量的代表元素
while (p != id[p]) p = id[p];
return p;
}
public void union(int p, int q)
{
int i = find(p);
int j = find(q);
if (i == j) return;
//分量连接
if (sz[i] < sz[j]) { id[i] = j; sz[j] += sz[i]; }
else { id[j] = i; sz[i] += sz[j]; }
count--;
}
public static void main(string[] args)
{
//某输入输出操作
}
}
同样,也需要对算法的最坏情况进行分析,最坏情况 如下图:

对于加权Quick-Union算法而言,其目的就是保证find操作的最高效率,也就是使得任意元素到达根节点的距离最短,这里直接给出结论:
在最坏的情况下,对于加权Quick-Union算法find、connected和union的成本数量级为logN。这使得该算法在处理大规模 数据时具有较好的效率。
在最坏情况下,各种Union-Find的增长数量级如下:
| 算法 | union | find |
|---|---|---|
| Quick-Find | N | N |
| Quick-Union | Height(树的高度) | Height(树的高度) |
| 加权Quick-Union | lgN | lgN |
| 使用路径压缩的加权Quick-Union | ~1(趋近1) | ~1(趋近1) |
原文:https://www.cnblogs.com/suanfawu/p/14386506.html