初见二叉树

第一次接触树,通过学习整理了一下内容:

  基本概念

定义:树形结构是一种非线性结构，它的特点是:每个结点最多只有一个前驱，但可以有多个后继。

如图我们可以做以下解释

双亲和孩子 :  若a是b的前驱，则称a是b的双亲，b是a的孩子。

兄弟:  若b和c有共同的前驱，则称b和c互为兄弟。

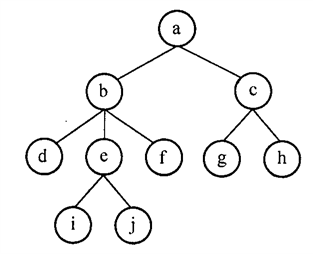
    分支结点和终端结点:  有后继的结点称为分支结点，没有后继的结点称为终端结点或树叶。

结点的度:  结点的度数等于该结点后继的个数。

    树的度:    树的度数等于树中结点度数的最大值。

结点的层:  结点的层次是从根结点开始定义的，根结点在第一层，其余结点的层次等于其双亲结点层次加1。

    树的高度:  树的高度等于树中结点层次的最大值。

1. 二叉树前序遍历:

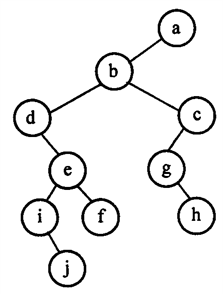
(1) 如上图得知遍历顺序为:abdeijfcgh(规律为根左右)

(2) 该遍历的算法如下:

递归 :   

void preorder(int p)

{

   if(p>0)//如果节点不为空的话我们进行if里面的代码程序

   {

     printf(“%c”, tree[p].data);//输出该节点

     preorder(tree[p].llink); //将下个节点输入该函数,递归输出剩余节点

     preorder(tree[p].rlink);

   }

}

1. 二叉树中序遍历:

(1) 如上图得知遍历顺序为:dijefbghca(规律为左根右)

(2) 该遍历的算法为:

递归:

    void inorder(int p)

{

   if(p>0)

   {

    inorder(tree[p].llink);//因为中序遍历的规律为:左根右所以先递归输出该节点的左孩子

    printf(“%c”, tree[p].data)

    inorder(tree(p).rlink);

   }

}

1. 二叉树后序遍历:

(1) 如上图得知遍历顺序为:jifedhgcba(规律为左右根)

(2) 该遍历的算法为:

递归:

void postorder(int p)

{

if(p>0)

{

      postorder(tree[p].llink); //因为该遍历的规律为左右根,所以先递归输出该点的左右孩子

  postorder(tree[p] .rlink);

    printf(“%c”, tree[p].data)

  }

}

存储二叉树的方法:我用的是以链表形式来存储这个二叉树,代码如下:

#define n0 100 //数组最大下标

#define datatype char

struct node{

   datatype data; //节点数值

   int llink,rimk;//左孩子和右孩子的指针

            };

node tree[n0+l];

int root; //根结点指针

如下图分别是一个二叉数和它在链表中静态存储结构:

初见二叉树

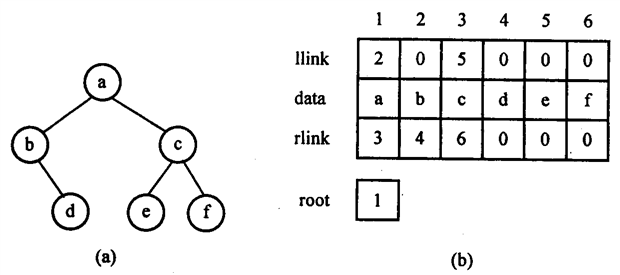
原文：https://www.cnblogs.com/zxy20020103/p/14387353.html