The new ITone 6 has been released recently and George got really keen to buy it. Unfortunately, he didn‘t have enough money, so George was going to work as a programmer. Now he faced the following problem at the work.
Given a sequence of n integers p1,?p2,?...,?pn. You are to choose k pairs of integers:
in such a way that the value of sum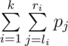 
is maximal possible. Help George to cope with the task.
The first line contains three integers n, m and k (1?≤?(m?×?k)?≤?n?≤?5000). The second line contains n integers p1,?p2,?...,?pn (0?≤?pi?≤?109).
Print an integer in a single line — the maximum possible value of sum.
5 2 1 1 2 3 4 5
9
7 1 3 2 10 7 18 5 33 0
61 题意：将一个长度为n的序列，分成k段长度为m的子序列，求这k个子序列和的最大值 思路：dp[i][j]表示是前i个数选出j段的最大值，显然有不选这个数，和考虑这个数的两种情况。而考虑这个数的话，因为连续性也只会增加以这个数为结尾的m序列#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> typedef long long ll; using namespace std; const int maxn = 5100; ll num[maxn], sum[maxn], dp[maxn][maxn]; ll n, m, k; int main() { cin >> n >> m >> k; for (int i = 1; i <= n; i++) { cin >> num[i]; sum[i] = sum[i-1] + num[i]; } for (int i = m; i <= n; i++) for (int j = k; j >= 1; j--) dp[i][j] = max(dp[i-1][j], dp[i-m][j-1]+sum[i]-sum[i-m]); cout << dp[n][k] << endl; return 0; }
Codeforces Round #267 (Div. 2) C. George and Job
原文：http://blog.csdn.net/u011345136/article/details/39405385