数据结构 - ST表

ST表简介

ST表是一种用来处理静态RMQ(Range Minimum/Maximum)问题的一种数据结构。即给一个长度为n的序列，以及m次询问，每次询问一个区间l，r中的最大值/最小值。我们虽然可以用线段树或者暴力求解，但在询问次数极多的情况下，不能很好的解决问题。今天，就让我们来学习一种 O（nlogn）时间预处理，O（1）查询的数据结构——ST表。

建立ST表

我们注意到一个重要的性质：求max的过程中，允许区间重叠。在同一区间内，max可以被重复计算。注意到这个性质，我们就可以开始建表了。我们设f[i][k]表示从i开始，往后第2^k个数组成的区间的最大值。自然，f[i][0]就是这个数本身。我们从数组的第1个数开始，依次往后递推出f[i][k]。我们可以发现出一个式子：f[i][k] = max(f[i][k - 1], f[1 + 2 ^ (k - 1)][k - 1])
这是为什么呢？我们通过一个图片来了解一下。

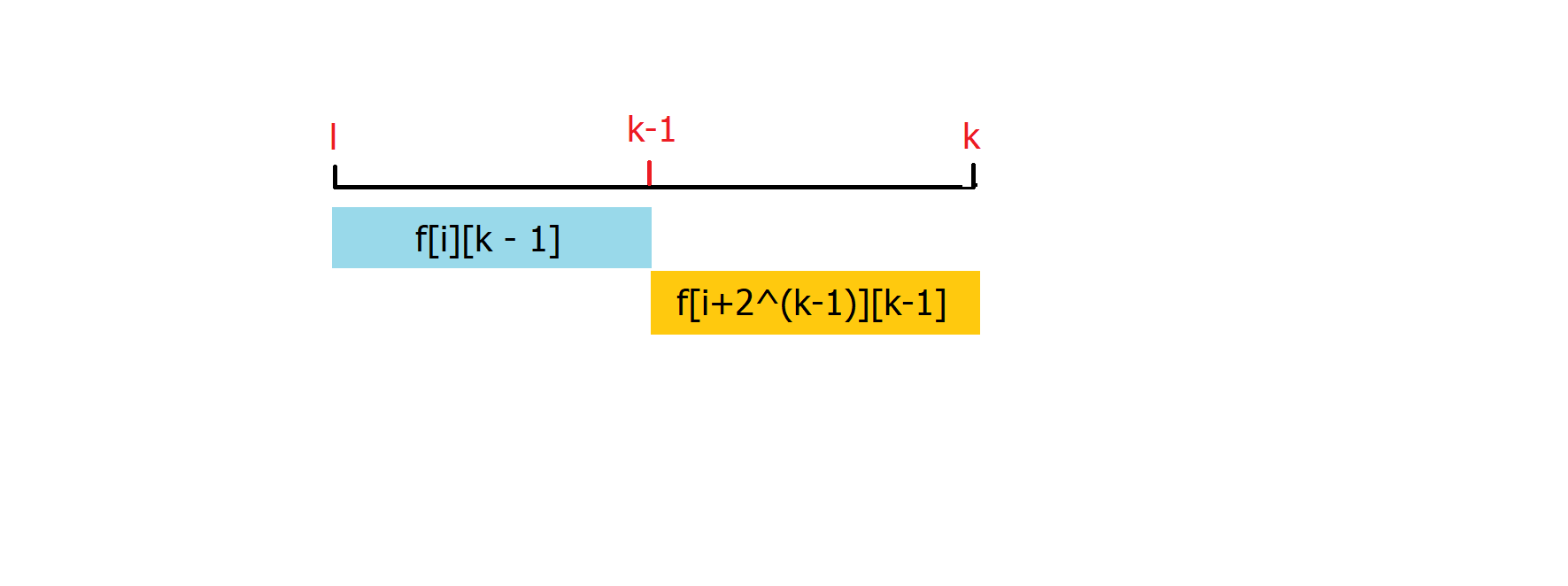
我们将一个大的f[i][k]拆分成两个小区间，每个区间长度都是2^(k - 1)，用区间Dp的思想来求解f[i][k]即可。
建立ST表的代码如下：

void build_ST()
{
  for (int j = 1; j <= 21; j ++ )
    for (int i = 1; i + (1 << j) - 1 <= n; i ++ )
      st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}

在实践中，我们通常把小的一维放在第一维，这样可以降低常数。

数据结构 - ST表

原文：https://www.cnblogs.com/ASUS-GWQSKY/p/14392165.html