【数位DP】度的数量

题面：https://www.acwing.com/problem/content/description/1083/

大意：求给定区间 \([X,Y]\) 中满足下列条件的整数个数：这个数恰好等于 \(K\) 个互不相等的 \(B\) 的整数次幂之和。

分析

dp(x)表示从 \(0-x\) 满足题意的数的个数。
那么接下来分情况讨论以分解问题：（设 \(x\) 有 \(n\) 位，在这里我们记最高位对应下标为 \(n-1\), 个位是 \(0\) ，同时记当前已经放了last个 \(1\) （那么当前还可以放置 k-last 个 \(1\)））

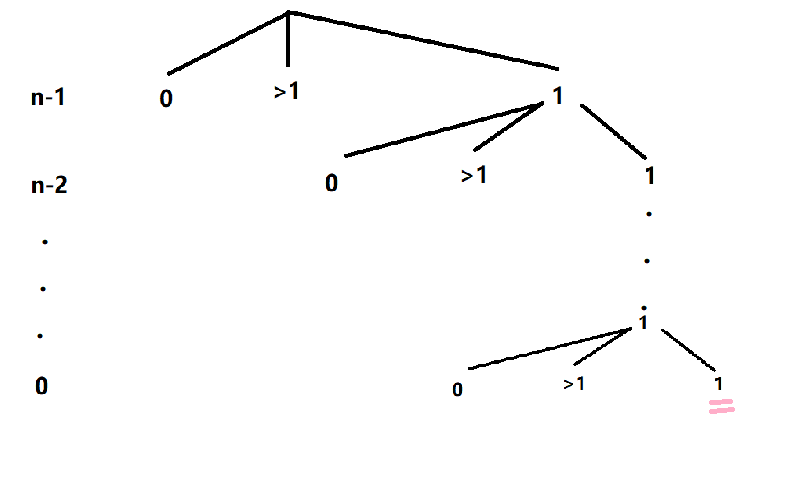
设当前位对应的下标是 \(i\)

• 如果当前位是 \(0\) ，那么它不会对 \(1\) 的个数造成任何影响，直接跳过。

• 如果当前位 \(>1\) （例如 \(i\) 和后面的数位组成了串 \(2488\) 那我们的任务则是求出 \(0-2488\) 有几个符合题意（因为前面数位的贡献已经统计好了）），那么相当于你有长度为 \(i+1\) 的串，只需从中选取 k-last 个 \(1\) 即可，对应的贡献为 \(C_{i+1}^{k-last}\)

• 如果当前位是 \(1\) 例如 \(i\) 和后面的数位组成了串 \(1488\) 那我们的任务则是求出 \(0-1488\) 有几个符合题意（因为前面数位的贡献已经统计好了），可以看出 \(0-999\) 的部分的贡献是 \(C_{3}^{k-last}\) ，而 \(1000-1488\) 的部分不易于在当前状态算出，故考虑转移到下一位继续统计，转移的时候last++，因为当前位是 \(1\)，在当前位放置了一个 \(1\) 。

这样我们便可以一层一层地向下计算下去了。

注意，在上图粉色部分是最后没有统计的，需要特殊考虑一下。

个人心得：做数位DP要时刻记得自己是对整个区间的数进行考虑，而不是单个数，并且在解题的时候要保证合理分划状态，保证统计时候的正确性。

代码：

#include<bits/stdc++.h>
using namespace std;

const int N=35;

//预处理求出组合数
int c[N][N];
void init(){
    for(int i=0;i<=N;i++)
        for(int j=0;j<=i;j++)
            if(!j) c[i][j]=1;
            else c[i][j]=c[i-1][j-1]+c[i-1][j];
}

int k,b;
int l,r;

int dp(int n){
    if(!n) return 0;
    
    vector<int> nums;
    while(n) nums.push_back(n%b),n/=b; //用nums储存b进制下的数码
    
    int res=0,last=0;
    for(int i=nums.size()-1;~i;i--){
        int x=nums[i]; //这里的x指n的最高位是 x

        //核心部分，开始分情况讨论
        if(x) //x>=1
        {
            if(x==1){
                if(k>=last) res+=c[i][k-last];
                last++;
                if(last>k) break;
            }else{
                if(k>=last) res+=c[i+1][k-last];
                break;
            }
        }
        
        if(i==0 && k==last) res++; //如果到了最后一位
    }
    return res;
}

int main(){
    init();
    cin>>l>>r>>k>>b;
    cout<<dp(r)-dp(l-1)<<endl; //类似于前缀和的思想
    return 0;
}

【数位DP】度的数量

原文：https://www.cnblogs.com/Tenshi/p/14398334.html