1、为什么要使用树结构
将数据使用树结构存储后,出奇的高效。
2、常用的数结构
二分搜索树(Binary Search Tree)
平衡二叉树: AVL; 红黑树
堆; 并查集
线段树; Trie(字典树,前缀树)
3、二叉树
和链表一样,动态数据结构
对于每一个节点,最多有两个孩子。
二叉树具有唯一根节点
叶子节点: 左右两个孩子都为空
每个节点,最多有一个父亲节点。
二叉树具有天然的递归结构,因为每个节点的左(右)子树也是二叉树。
class Node {
E e;
Node left; //左孩子
Node right; //右孩子
}
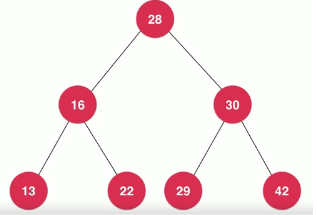
二叉树不一定是满的,如下图所示
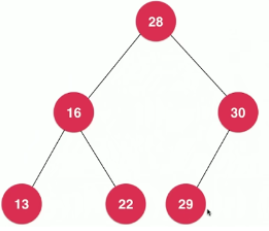
图1
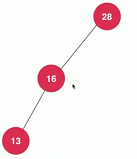
图2
一个节点也是二叉树

NULL 空也是二叉树
4、二分搜索树Binary Search Tree
二分搜索树是二叉树
二分搜索树的每个节点值,大于其左子树所有节点的值,小于其右子树的所有节点的值。
每一棵子树也是二分搜索树。
存储的元素必须有可比较性(如这里使用的是数字)
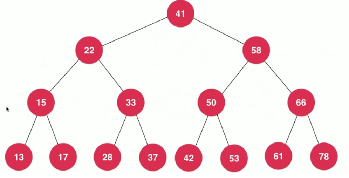
二分搜索树不一定是满的。如下图所示
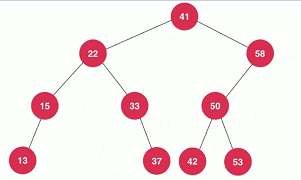
4.1 二分搜索树的
public class BinarySearchTree<E extends Comparable<E>> {
private class Node{
public E e;
//左孩子
public Node left;
//右孩子
public Node right;
public Node(E e){
this.e = e;
left = null;
right = null;
}
}
// 跟元素
private Node root;
//数节点的个数
private int size;
public BinarySearchTree(){
root = null;
size = 0;
}
public int size(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
}
4.2 向搜索二叉树添加元素
对根元素做特殊处理。
//向二分搜索树中添加新的元素e
public void add(E e){
if(root == null){
root = new Node(e);
size ++;
}else{
add(root, e);
}
}
//向以node为根的二分搜索树种插入元素e,递归算法
public void add(Node node, E e){
if(e.equals(node.e)){
return;
}else if(e.compareTo(node.e) < 0 && node.left == null){
node.left = new Node(e);
size ++;
return;
}else if(e.compareTo(node.e) > 0 && node.right == null){
node.right = new Node(e);
size ++;
return;
}
if(e.compareTo(node.e) < 0 ){
add(node.left, e);
}else {
add(node.right, e);
}
}
4.3 对 3.2 向搜索二叉树添加元素进行改进
//向二分搜索树中添加新的元素e
public void add(E e){
root = add(root, e);
}
//向以node为根的二分搜索树种插入元素e,递归算法
public Node add(Node node, E e){
if(node == null){
size ++;
return new Node(e);
}
if(e.compareTo(node.e) < 0){
node.left = add(node.left, e);
}else if(e.compareTo(node.e) > 0){
node.right = add(node.right, e);
}
return node;
}
4.4 二分搜索树的查询操作
//看二分搜索树种是否包含元素e
public boolean contains(E e){
return contains(root, e);
}
//看以node为根的二分搜索树中是否包含元素e,递归算法
public boolean contains(Node node, E e){
if(node == null){
return false;
}
if(e.compareTo(node.e) == 0){
return true;
}else if(e.compareTo(node.e) < 0){
return contains(node.left, e);
}else {
return contains(node.right, e);
}
}
4.5 二分搜索树前序遍历
//二分搜索树前序遍历
public void preOrder(){
preOrder(root);
}
//前序遍历以node为根的二分搜索树,递归算法
public void preOrder(Node node){
if(node == null){
return;
}
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
前序遍历测试
public static void main(String[] args) {
BinarySearchTree<Integer> bst = new BinarySearchTree<Integer>();
int [] nums = {5,3,6,8,4,2};
for(int num :nums){
bst.add(num);
}
//////////////////////////
///////// 5 /////////
///////// / \ //////////
// 3 6 //
// / \ \ ///
// 2 4 8 //
//////////////////////////
bst.preOrder();
System.out.println();
}
输出结果:
5
3
2
4
6
8
4.6 二分搜索树的中序遍历和后序遍历
//二分搜索树中序遍历
public void inOrder(){
inOrder(root);
}
//中序遍历以node为根的二分搜索树,递归算法
private void inOrder(Node node){
if(node == null){
return;
}
inOrder(node.left);
System.out.println(node.e);
inOrder(node.right);
}
测试:
public static void main(String[] args) {
BinarySearchTree<Integer> bst = new BinarySearchTree<Integer>();
int [] nums = {5,3,6,8,4,2};
for(int num :nums){
bst.add(num);
}
//////////////////////////
///////// 5 /////////
///////// / \ //////////
// 3 6 //
// / \ \ ///
// 2 4 8 //
//////////////////////////
//中序遍历
bst.inOrder();
System.out.println();
}
结果:
2
3
4
5
6
8
可以看出,中序遍历结果是顺序的。
同理,后序遍历
代码如下:
//二分搜索树后序遍历
public void postOrder(){
postOrder(root);
}
//后序遍历以node为根的二分搜索树,递归算法
private void postOrder(Node node){
if(node == null){
return;
}
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
}
测试:
public static void main(String[] args) {
BinarySearchTree<Integer> bst = new BinarySearchTree<Integer>();
int [] nums = {5,3,6,8,4,2};
for(int num :nums){
bst.add(num);
}
//////////////////////////
///////// 5 /////////
///////// / \ //////////
// 3 6 //
// / \ \ ///
// 2 4 8 //
//////////////////////////
//后续遍历
bst.postOrder();
System.out.println();
}
输出结果:
2
4
3
8
6
5
后序遍历的一个应用场景: 手工为二分搜索树释放内存(如C++),先释放所有的孩子节点,再释放根节点。
4.7 二分搜索树的非递归前序遍历
//二分搜索树的非递归前序遍历
public void preOrderNR(){
Stack<Node> stack = new Stack<Node>();
stack.push(root);
while (!stack.isEmpty()){
Node cur = stack.pop();
System.out.println(cur.e);
if (cur.right != null){
stack.push(cur.right);
}
if(cur.left != null){
stack.push(cur.left);
}
}
}
4.8 二分搜索树的层序遍历(广度优先遍历)
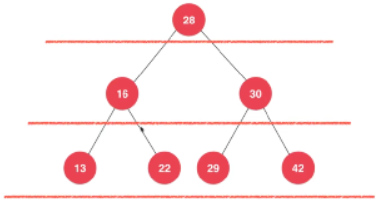
28 15 30 13 22 29 42
层序遍历实现
//二分搜索树的层序遍历
public void levelOrder(){
Queue<Node> q = new LinkedList<Node>();
q.add(root);
while (!q.isEmpty()){
Node cur = q.remove();
System.out.println(cur.e);
if(cur.left != null){
q.add(cur.left);
}
if(cur.right != null){
q.add(cur.right);
}
}
}
测试:
public static void main(String[] args) {
BinarySearchTree<Integer> bst = new BinarySearchTree<Integer>();
int [] nums = {5,3,6,8,4,2};
for(int num :nums){
bst.add(num);
}
//////////////////////////
///////// 5 /////////
///////// / \ //////////
// 3 6 //
// / \ \ ///
// 2 4 8 //
//////////////////////////
//层序遍历
bst.levelOrder();
System.out.println();
}
输出结果:
5
3
6
2
4
8
广度优先遍历的意义
更快的找到问题的解
常用于算法设计中-最短路径
图中的深度优先遍历和广度优先遍历
4.9 删除二分搜索树的最大元素和最小元素
//寻找最小节点
public E minimum(){
if(size == 0){
throw new IllegalArgumentException("Bst is empty");
}
return minimum(root).e;
}
//返回以Node为根的二分搜索树的最小值的节点
public Node minimum(Node node){
if(node.left == null){
return node;
}
return minimum(node.left);
}
//寻找最大节点
public E maximum(){
if(size == 0){
throw new IllegalArgumentException("Bst is empty");
}
return maximum(root).e;
}
//返回以Node为根的二分搜索树的最大值的节点
public Node maximum(Node node){
if(node.right == null){
return node;
}
return maximum(node.right);
}
// 从二分搜索树中删除最小值所在节点, 返回最小值
public E removeMin(){
E ret = minimum();
root = removeMin(root);//注意这里,我们从root为根的树中删除掉了最小值,返回删除后的树的根节点,这个
//根节点就是新的root
return ret;
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node){
// 递归的终止条件,当前节点没有左子树了,那么就是最小节点了
// 如果是最小节点,我们要做的是删除当前节点,但是当前节点很可能是有右子树的
// 我们先把该节点的右子树节点保存,然后就删除掉该右子树节点,最后把右子树节点返回即可
if(node.left == null){
Node rightNode = node.right;
node.right = null;//左节点为空了,让右子树也为空,相当于脱离了树
size --;
return rightNode;//返回右子树是为了后面的绑定操作
}
// 没有递归到底的情况,那么就递归调用其左子树,这个调用的过程会返回被删除节点的右子树,
//将返回的右子树重新绑定到上一层的node的左节点上就相当于彻底删除了那个元素
node.left = removeMin(node.left);
return node; // 删除后,根节点依然是node,返回即可
}
// 从二分搜索树中删除最大值所在节点
public E removeMax(){
E ret = maximum();
root = removeMax(root);
return ret;
}
// 删除掉以node为根的二分搜索树中的最大节点
// 返回删除节点后新的二分搜索树的根
private Node removeMax(Node node){
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
4.10 删除二分搜索树的任意元素
删除左右都有孩子的节点
d为要删除的节点。
找到 s = min(d-> right) d的右孩子中最小的节点,这里为59
s是d的后继。
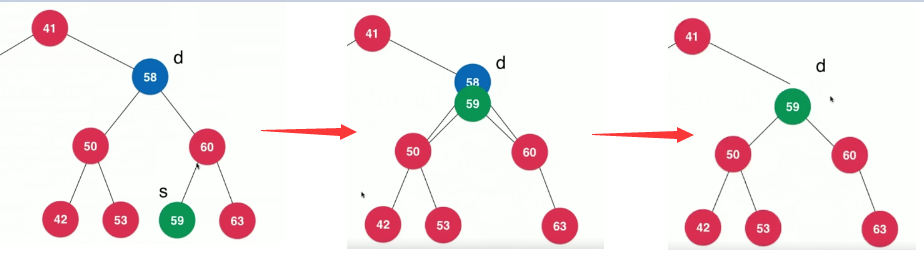
代码实现:
//从二分搜索树中删除元素为e的节点
public void remove(E e) {
root = remove(root, e);
}
//删除以node为根的二分搜索树中值为e的节点,递归算法
// 返回要删除节点后新的二分搜索树的根
private Node remove(Node node, E e) {
if (node == null) {
return null;
}
if (e.compareTo(node.e) < 0) {
node.left = remove(node.left, e);
}
if (e.compareTo(node.e) > 0) {
node.right = remove(node.right, e);
} else { // e == node.e
// 待删除节点左子树为空
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
// 待删除节点右子树为空
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
// 待删除的节点左右子树均不为空
// 找到比待删除节点大的最小节点,即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
return null;
}
原文:https://www.cnblogs.com/linlf03/p/14397423.html