Is Graph Bipartite? (M)

题目

Given an undirected graph, return true if and only if it is bipartite.

Recall that a graph is bipartite if we can split its set of nodes into two independent subsets A and B, such that every edge in the graph has one node in A and another node in B.

The graph is given in the following form: graph[i] is a list of indexes j for which the edge between nodes i and j exists. Each node is an integer between 0 and graph.length - 1. There are no self edges or parallel edges: graph[i] does not contain i, and it doesn‘t contain any element twice.

Example 1:

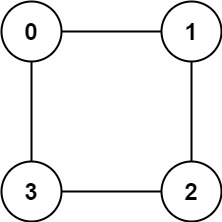
Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can divide the vertices into two groups: {0, 2} and {1, 3}.

Example 2:

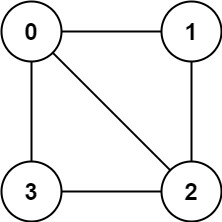
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: We cannot find a way to divide the set of nodes into two independent subsets.

Constraints:

• 1 <= graph.length <= 100
• 0 <= graph[i].length < 100
• 0 <= graph[i][j] <= graph.length - 1
• graph[i][j] != i
• All the values of graph[i] are unique.
• The graph is guaranteed to be undirected.

题意

给定一个图，将其中结点划分为两个集合，使得每条边的两个结点分属于两个不同的集合。

思路

直接用BFS或DFS遍历所有结点，将当前结点的所有邻接结点标记为与当前结点不一样的值，如果出现两个相邻结点被标记为相同的值则返回false。注意给的图不一定是连通图。

代码实现

Java

class Solution {
    public boolean isBipartite(int[][] graph) {
        int[] color = new int[graph.length];

        for (int i = 0; i < graph.length; i++) {
            if (color[i] != 0) continue;
            color[i] = 1;
            Queue<Integer> q = new ArrayDeque<>();
            q.offer(i);
            while (!q.isEmpty()) {
                int cur = q.poll();
                for (int next : graph[cur]) {
                    if (color[next] == color[cur]) return false;
                    if (color[next] == 0) {
                        color[next] = 3 - color[cur];
                        q.offer(next);
                    }
                }
            }
        }

        return true;
    }
}

0785. Is Graph Bipartite? (M)

原文：https://www.cnblogs.com/mapoos/p/14402752.html