平衡二叉树仍然是一棵二叉查找树,只是在其基础上增加了“平衡”要求
平衡是指:对AVL树的任意结点来说,其左子树与右子树的高度之差的绝对值不超过1
其中左子树与右子树的高度之差称为该结点的平衡因子
由于需要对每个结点都得到平衡因子,因此需要在树的结构中加入一个变量height,用以记录以当前结点为根结点的子树的高度
struct node{ int data,height; //data为结点权值,height为当前结点高度 node* lchild,*rchild; //左右孩子结点地址 };
node* newNode(int v) { node* Node=new node; //申请一个node型变量的地址空间 Node->data=v; Node->height=1; //结点高度初始化为1 Node->lchild=Node->rchild=NULL; //初始状态下没有左右孩子 return Node; }
int getHeight(node* root) { if(root==NULL) return 0; //空结点,高度为0 return root->height; }
int getBalanceFactor(node* root) { //左子树高度减右子树高度 return getHeight(root->lchild)-getHeight(root->rchild); }
//结点root所在子树的height等于其左子树的height与右子树的height的较大值加1 void updateHeight(node* root) { root->height=max(getHeight(root->lchild),getHeight(root->rchild))+1; }
//由于AVL树高度为O(logn)级别,因此AVL树的查找操作时间复杂度为O(logn) //search函数查找AVL树中数据域为x的结点 void search(node* root,int x) { if(root==NULL){ //空树,查找失败 printf("search failed!\n"); return; } if(x==root->data){ printf("%d\n",root->data); }else if(x<root->data){ search(root->lchild,x); //往左子树搜索x }else{ search(root->rchild,x); } }
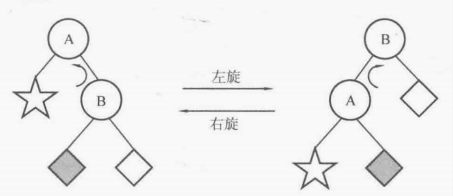
/* ①让B的左子树成为A的右子树 ②让A成为B的左子树 ③将根结点设为结点B */ void L(node* &root) { node* temp=root->rchild; root->rchild=temp->lchild; temp->lchild=root; updateHeight(root); updateHeight(temp); root=temp; }
/* ①让A的右子树成为B的左子树 ②让B作为A的右子树 ③将根结点设为结点A */ void R(node* &root) { node* &temp=root->lchild; root->lchild=temp->rchild; temp->rchild=root; updateHeight(root); updateHeight(temp); root=temp; }
①讨论结点A的平衡因子是2的情形(左子树的高度比右子树大2),于是以结点A为根结点的子树一定是图9-31的两种形态LL型与LR型之一,
当结点A的左孩子的平衡因子是1时为LL型,是-1时为LR型。
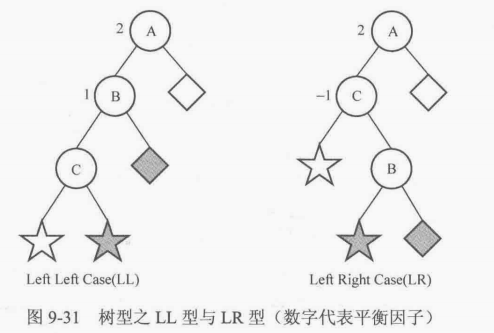
现在考虑怎样调整这两种树型,才能使树平衡。
先考虑LL型,可以把以C为根结点的子树看作一个整体,然后以结点A作为root进行右旋,便可以达到平衡,如图9-32所示。
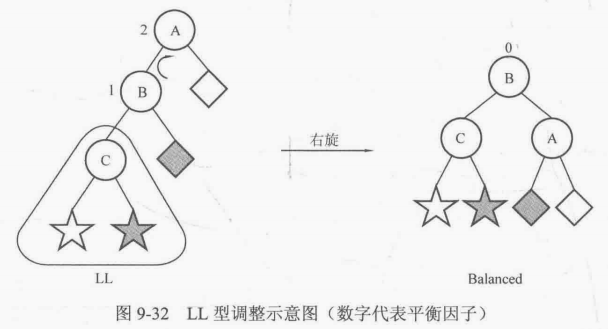
然后考虑LR型,可以先忽略结点A,以结点C为root进行左旋,再按LL型做法进行一次右旋,如图9-33所示。
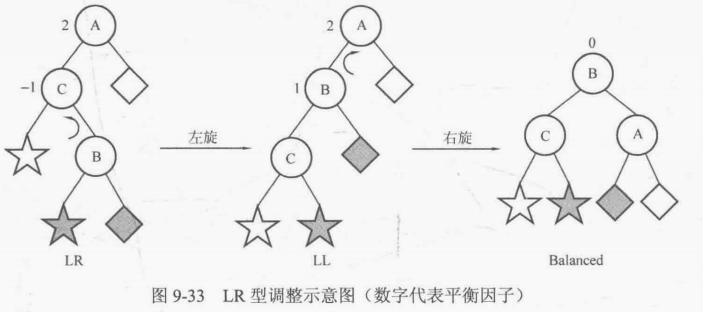
②考虑平衡因子为-2的情形(右子树高度比左子树大2),以结点A为根结点的子树一定是图9-34的两种形态RR型与RL型之一,当结点A的右孩子的平衡因子是-1时为RR型,是1时为RL型。
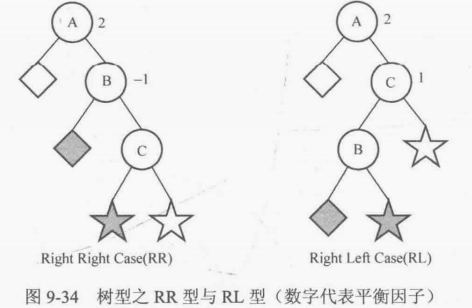
对RR型来说,可以把以C为根结点的子树看做一个整体,然后以结点A作为root进行左旋,便可达到平衡,如图9-35所示。
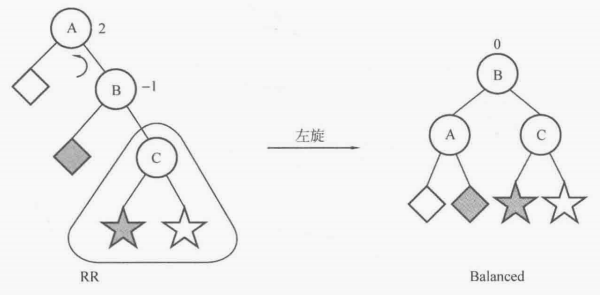
对RL型来说,可以先忽略结点A,以结点C为root进行一次右旋,再按照RR型做法进行一次左旋,如图9-36所示。
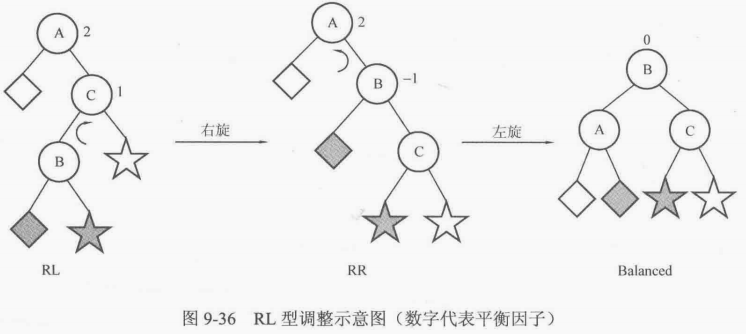
AVL树插入情况总结如下(BF表示平衡因子)

现在考虑书写插入代码,首先,AVL树的插入代码是在二叉树的插入代码基础上增加平衡操作的,因此,如果不考虑平衡操作,代码是这样的:
//插入权值为v的结点 void insert(node* &root,int v) { if(root==NULL) //到达空结点 { root=newNode(v); return; } if(v<root->data) //v比根结点的权值小 { insert(root->lchild,v); //往左子树插入 }else //v比根结点的权值大 { insert(root->rchild,v); //往右子树插入 } }
在这个基础上,由于需要从插入的结点开始从下往上判断结点是否失衡,因此需要在每一个insert函数之后更新当前结点的高度,并在这之后根据树形是LL型、LR型、RR型、RL型之一来进行平衡操作。代码如下:
//AVL树插入代码 //插入权值为v的结点 void insert(node* &root,int v) { if(root==NULL){ //到达空结点 root=newNode(v); return; } if(v<root->data){ //v比根结点权值小 insert(root->lchild,v); //往左子树插入 updateHeight(root); //更新树高 if(getBalanceFactor(root)==2){ if(getBalanceFactor(root->lchild)==1){ //LL型 R(root); }else if(getBalanceFactor(root->lchild)==-1){ //LR型 L(root->lchild); R(root); } } }else{ //v比根结点的权值大 insert(root->rchild,v); //往右子树插入 updateHeight(root); //更新树高 if(getBalanceFactor(root)==-2){ if(getBalanceFactor(root->rchild)==-1){ //RR型 L(root); }else if(getBalanceFactor(root->lchild)==1){ //RL型 R(root->rchild); L(root); } } } }
node* Create(int data[],int n) { node* root=NULL; //新建空根结点root for(int i=0;i<n;i++) { insert(root,data[i]); //将data[0]~data[n-1]插入AVL树中 } return root; //返回根结点 }
原文:https://www.cnblogs.com/jianqiao123/p/14405844.html