一、数据结构
1)数据结构的定义
我们如何把现实中大量而且非常复杂的问题以特定的数据类型(个体)和特定的存储结构(个体的关系)保存到相应的相应的主存储器(内存)中, 以及在此基础上为实现某个功能而执行的相应操作,这个相应的操作也叫做算法 数据结构 == 个体 + 个体的关系 算法 == 对存储数据的操作
2)数据结构的特点
程序=数据的存储+数据的操作+可以被计算机执行的语言
二、排序 LOW B 三人组
冒泡排序 选择排序 插入排序 时间复杂度:O(n2) 空间复杂读:O(1)
1)冒泡排序

def BubbleSort(li): for i in range(len(li) -1): for j in range(len(li) -i -1): if li[j] > li[j+1]: li[j],li[j+1] = li[j+1],li[j] li = [7,5,4,6,3,8,2,9,1] BubbleSort(li) print(li)
1.1)对应冒泡排序的优化。如果冒泡排序中执行一趟而没有交换,则列表已经是有序状态,可以直接结束算法

def bubble_sort(li): for i in range(len(li) -1): exchange = False for j in range(len(li) -i -1): if li[j] > li[j+1]: li[j],li[j+1]=li[j+1],li[j] exchange = True if not exchange: return li = [1, 2, 3, 4, 5, 6, 7, 9, 8] bubble_sort(li) print(li)
2)选择排序

def selectSort(li): for i in range(len(li) - 1): minLoc = i for j in range(i, len(li)): if li[j] < li[minLoc]: li[j], li[minLoc] = li[minLoc], li[j] li = [7, 5, 4, 6, 3, 8, 2, 9, 1] selectSort(li) print(li)
3)插入排序
列表被分为有序区和无序区两个部分。最初有序区只有一个元素
每次从无序区选择一个,插入到有序区的位置,知道无序区变空
代码演示

def insertSort(li): for i in range(1, len(li)): tmp = li[i] j = i - 1 while j >= 0 and tmp < li[j]: li[j + 1] = li[j] j = j - 1 # j = -1 li[j + 1] = tmp li = [7, 5, 4, 6, 3, 8, 2, 9, 1] insertSort(li) print(li)
三、排序 NB
1)快排。 时间(n*log n)
快速排序:快
快写的排序算法里最快的
快的排序算法里最好写的
快排思路:
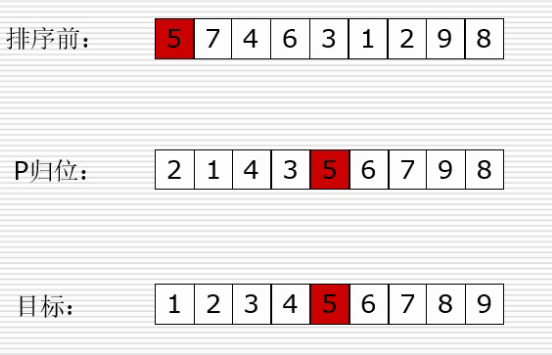
取一个元素P(第一个元素),使元素p归位
列表被P分为了两部分,左边都比P小,右边都比P大
递归完成排序
代码演示

def partition(li,left,right): tmp = li[left] while left < right: while left < right and li[right] >= tmp: right = right - 1 li[left] = li[right] while left < right and li[left] <= tmp: left = left + 1 li[right] = li[left] li[left] = tmp return left def quickSort(li,left,right): if left < right: mid = partition(li,left,right) quickSort(li,left,mid-1) quickSort(li,mid+1,right) li = [7, 5, 4, 6, 3, 8, 2, 9, 1] quickSort(li,0,len(li)-1) print(li)
1.1)模拟大数据进行排序,冒泡排序与快排的时间差
冒泡排序测试

import random,time def BubbleSort(li): for i in range(len(li) - 1): for j in range(len(li) - i - 1): if li[j] > li[j + 1]: li[j], li[j + 1] = li[j + 1], li[j] li = [random.randint(1,100) for i in range(10000)] start_time = time.time() BubbleSort(li) print(‘costtime is :‘,time.time()-start_time)
用时: costtime is : 7.353521823883057
快速排序测试

import random,time,sys sys.setrecursionlimit(3000000) def partition(li, left, right): tmp = li[left] while left < right: while left < right and li[right] >= tmp: right = right - 1 li[left] = li[right] while left < right and li[left] <= tmp: left = left + 1 li[right] = li[left] li[left] = tmp return left def quickSort(li, left, right): if left < right: mid = partition(li, left, right) quickSort(li, left, mid - 1) quickSort(li, mid + 1, right) li = [random.randint(1,100) for i in range(10000)] start_time = time.time() quickSort(li, 0, len(li) - 1) print(‘costtime is :‘,time.time()-start_time)
快排: costtime is : 0.047846078872680664
2)归并排序。时间(n*log n)
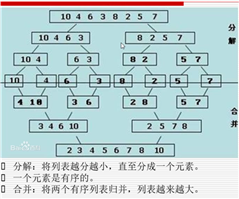
代码演示

def merge(li, left, mid, right): i = left j = mid + 1 ltmp = [] while i <= mid and j <= right: if li[i] < li[j]: ltmp.append(li[i]) i = i + 1 else: ltmp.append(li[j]) j = j + 1 while i <= mid: ltmp.append(li[i]) i = i + 1 while j <= right: ltmp.append(li[j]) j = j + 1 li[left:right + 1] = ltmp def mergeSort(li, left, right): if left < right: mid = (left + right) // 2 mergeSort(li, left, mid) mergeSort(li, mid + 1, right) print(‘归并之前‘, li[left:right + 1]) merge(li, left, mid, right) print(‘归并之后‘, li[left:right + 1]) li = [10, 4, 6, 3, 8, 2, 5, 7] mergeSort(li, 0, len(li) - 1)
3)希尔排序

第一次变化
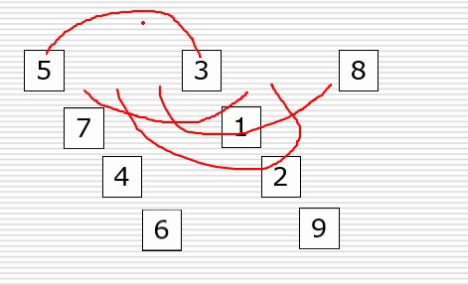
第二次变化
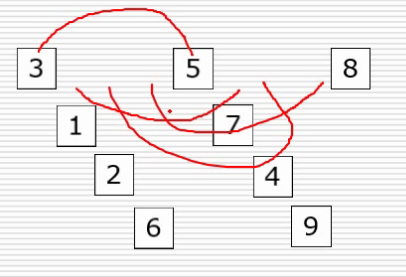
第二次变化的合并值为(依次循环)
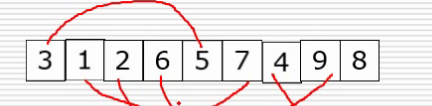
代码

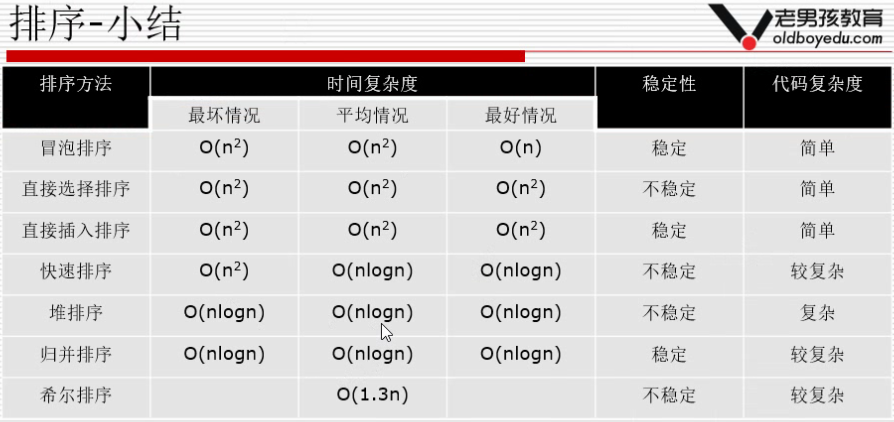
快速排序、堆排序、归并排序-小结 三钟排序算法的时间复杂度都是 O(nlogn) 一般情况下,就运行时间而言: 快速排序 < 归并排序 < 堆排序 三种排序算法的缺点: 快速排序:极端情况下排序效率低 归并排序,需要额外的内存开销 堆排序:在快的排序算法中相对较慢
三、练习
1)计数排序
问题:现在有一个列表,列表中的数范围都在0到100之间,列表长度大约为100万。
设计算法在O(n)时间复杂度内将列表进行排序
计数算法代码示例

def countSort(li): count = [0 for i in range(11)] for x in li: count[x] += 1 # print(count) li.clear() for index, val in enumerate(count): # print(index, val) for j in range(val): li.append(index) li = [10, 4, 6, 3, 8, 2, 5, 7] countSort(li) print(li)


原文:https://www.cnblogs.com/linu/p/11139716.html