参考:链接
1、定义在非空有限集合上的偏序集合 L,满足集合 L 中的任意元素 a,b,使得 a,b 在 L 中存在一个最大下界,和最小上界。
2、群论中的定义,是 RnRn 中的满足某种性质的子集。当然,也可以是其它群。
1、格中计算问题的困难性,即这些问题的计算复杂性,主要有:
2、如何求解格中的困难性问题,目前既有近似算法,也有一些精确性算法。
3、基于格的密码分析,即如何利用格理论分析一些已有的密码学算法,目前有如下研究:
4、如何基于格困难问题设计新的密码体制,这也是后量子密码时代的重要研究方向之一,目前有以下研究:
参考:链接
| 时间 | 标志事件 |
|---|---|
| 18世纪–1982年 | 格经典数学问题的讨论,代表人物:Lagrange,Gues,Hermite,MInkowski等 |
| 1982年–1996年 | 期间标志性事件是LLL算法的提出(Lenstra-Lenstra-Lovasz) |
| 1996年–2005年 | 第一代格密码诞生(Ajtai96, AD97G, GH9) |
| 2005年–2016年 | 第二代格密码出现并逐步完善,并实用化格密码算法 (Regev05, GPV08,MP12 BLISS ,NewHope, Frodo) |
| 2016年– | 格密码逐步得以标准化 |
发展:
| 从前 | 现在 | |
|---|---|---|
| 具有悠久历史的格经典数学问题的研究 | ? |
近30多年来高维格困难问题的求解算法及其计算复杂性理论研究 |
| 使用格困难问题的求解算法分析非格公钥密码体制的安全性 | ? | 基于格困难问题的密码体制的设计 |
优势:
| 格密码 | 经典密码 |
|---|---|
| 量子攻击算法 | Shor算法 |
| 矩阵乘法、多项式乘法 | Shor算法 |
| Worst-case hardness | Average-case hardnes |
| 结构灵活、功能丰富 | 结构简单、功能受限 |

简而言之,格是n个线性无关向量的所有整系数的线性组合
1、det(A)
指方阵A的行列式
2、向量范数


3、基础区域 F
一个格L的任何基础区域都有着相同的 “体积”
下面的平行四边形即为一个【基础区域F】
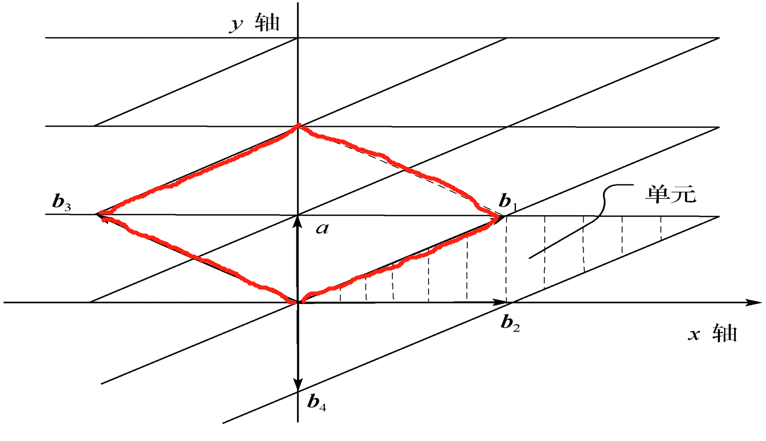
基础区域 F 的n维体积称为 L 的行列式,记为det L
4、Hadamard 不等式
L是一个格,任意一个基![]() 和基础区域 F ,有
和基础区域 F ,有
det L = vol(F)≤ || v1|| || v2|| .....|| vm|| ,基向量![]() 越接近垂直,等式越成立
越接近垂直,等式越成立
vol(F)是F的体积
5、dim(L)
格的维度,即格的基中的向量个数
6、Hadamard比率
用于描述一组向量的正交程度
格的基 B ={v1,v2,...,vn},有

0< H(B)≤1,且越接近1,则基中的向量就越接近两两正交
matlab代码实现:
function [result] = H(m)
% 计算一组基的Hadamard比率
% 输入:基向量作为行向量所构成的方阵
% 输出:当前基的Hadamard比率
% 1、取出矩阵中的每个行向量
% 2、按照Hadamard比率公式计算
% 3、返回计算结果
n = size(m); %m是矩阵,size返回矩阵维度(行,列)
n = n(1); %取行
product = 1;
for i = 1:n
product = product * norm(m(i,:)); % norm求每个行向量的向量范数,product是 ||v1|| ||v2|| ... ||vn||
end
result = (abs(det(m)) / product^1/n); %abs取绝对值,det是矩阵的行列式
end
7、格基相互转化
格L的任意两个基可以通过在左边乘上一个特定的矩阵来相互转化,这个矩阵由整数构成,且它的行列式为 ±1
8、生成优质基
随机生成满足Hadamard比率的优质基
matlab代码实现:
function result = good_basis(N,v,h)
% 随机生成一组优质基
% N是基向量的坐标的绝对值上限,v是向量的个数(格的维度),h是Hadamard比率的下限
% 输入:向量中坐标的取值下限,基中向量的个数,Hadamard比率的下限
% 输出:矩阵形式的优质基
% 1、根据取值下限和维度,随机生成矩阵
% 2、调用H()计算Hadamard比率
% 3、若比率大于下限,则返回该矩阵,否则跳转1
result = unidrnd(2*N,v) - N; %unidrnd 返回随机方阵
while H(result) < h
result = unidrnd(2*N,v) - N;
end
end
9、计算矩阵行范数
matlab代码实现:
function [result] = row_norm(m)
%计算一个矩阵的行范式
% 输入:矩阵形式的一组基
% 输出:一个包含每一个行向量范数的列向量
% 1、取出矩阵中的每个行向量
% 2、计算每个行向量的范数
% 3、返回计算结果
n = size(m);
result = zeros(n(1),1); % 返回一个全0的矩阵(n(1)行,1列)
for i = 1:n(1)
result(i,1) = norm(m(i,:)); % 每个列向量的第一个位向量范数
end
end
10、向量正交化
施密特正交化:

matlab代码实现:
function [M] = orthogonal(m)
% 使用施密特正交化对矩阵m以行为单位进行正交化,并未单位化
% 输入:矩阵形式的一组基
% 输出:正交化后的矩阵
n = size(m);
M = zeros(n);
n = n(1);
M(1,:) = m(1,:);
for i = 2:n
M(i,:) = m(i,:);
for j = 1:i-1
u_ij = dot(m(i,:),M(j,:)) / (norm(M(j,:))^2);
M(i,:) = M(i,:) - u_ij * M(j,:);
end
end
end
最基本的难题SVP和CVP,其他的困难问题可由这两种问题变形得到。
Shortest Vector Problem,最短向量问题
在格中寻找一个最短的非零向量,即寻找一个向量 v∈ L,使得它的欧几里得范数 ||v|| 最小
问题:一个格的最短非零向量多长?
高斯期望(高斯启发式)可以求出最短向量问题
Closest Vector Problem,最近向量问题
给定一个不在格L中的向量 t∈Rm ,寻找一个向量 v∈ L,使得它最接近w,即寻找一个向量 v∈ L,使得它的欧几里得范数 ||w - v|| 最小
问题:如何使向量接近两两正交的基来求解最近向量问题?
方法1:寻找顶点法
“优基”适合,“劣基”不合适
方法2:
Babai算法

功能:将一个劣质基转换成一个优质基,且优质基中的第一个行向量就是格中的最短非零向量
算法为两部分:
劣质基会变得更优,且基中向量的范数也会适当的减小

matlab代码实现:
function [result] = LLL(v)
% 格基约减的控制算法,对矩阵处理,v是每行的行向量
% 输入:矩阵形式的一组基
% 输出: 约减一次后的基
a = LLL_if(v);
b= LLL_if(a);
while a ~= b % a和b不同时
a = b;
b = LLL_if(b);
end
result = b;
end
控制基格约减的循环条件
matlab代码实现:
function [result] = LLL_if(v)
% LLL约减算法
% 输入:矩阵形式的一组基
% 输出:约减后的基
% 1、对输入参数,调用LLL()
% 2、对1的结果再次调用LLL()
% 3、重复2,直到结果不再变化
% 4、返回不再变化的结果
n = size(v);
n = n(1);
k = 2;
while k <= n
V = orthogonal(v(1:k,:));
for j = 1:k-1
u = dot(v(k,:),V(j,:)) / (norm(V(j,:))^2);
v(k,:) = v(k,:) - round(u) * v(l,:);
end
u = dot(v(k,:),V(k-1,:)) / (norm(V(k-1,:))^2);
if norm(V(k,:))^2 >= (3/4 - u^2) * norm(V(k-1,:))^2
k = k + 1;
else
temp = v(k-1,:);
v(k-1,:) =v(k,:);
v(k,:) = temp;
k = max(k-1,2);
end
end
result = v;
return;
end
原文:https://www.cnblogs.com/pam-sh/p/14265017.html