本文内容为https://zhuanlan.zhihu.com/p/77151308的总结
PCA(Principal Component Analysis) 是一种常见的数据分析方式,常用于高维数据的降维,可用于提取数据的主要特征分量。
PCA 的数学推导可以从最大可分型和最近重构性两方面进行,前者的优化条件为划分后方差最大,后者的优化条件为点到划分平面距离最小,这里我将从最大可分性的角度进行证明。
1. 基本知识
1.1 内积:首先是 A 与 B 的内积值等于 A 向 B 所在直线投影的标量大小。(B长度为1的情况下)
1.2 基:要准确描述向量,首先要确定一组基,然后给出在基所在的各个直线上的投影值,就可以了
1.3 基变换的矩阵表示:两个矩阵相乘的意义是将右边矩阵中的每一列向量 变换到左边矩阵中以每一行行向量为基所表示的空间中去
2. 最大可分性
直观来讲我们希望投影后的投影值尽可能分散,因为如果重叠就会有样本消失。当然这个也可以从熵的角度进行理解,熵越大所含信息越多。
2.1 方差:一维空间中我们可以用方差来表示数据的分散程度。上述问题的两个方向中的其中一个为:寻找一个一维基,使得所有数据变换为这个基上的坐标表示后,方差值最大。
2.2 协方差:表示两个变量的线性相关性。为了让两个变量尽可能表示更多的原始信息,我们希望它们之间不存在线性相关性,因为相关性意味着两个变量不是完全独立,必然存在重复表示的信息。
2.3 协方差矩阵:最终要达到的目的与变量内方差及变量间协方差有密切关系。因此我们希望能将两者统一表示,仔细观察发现,两者均可以表示为内积的形式,而内积又与矩阵相乘密切相关。所以我们干脆用协方差矩阵表示两者。设协方差矩阵 ,则 C 是一个对称矩阵,其对角线分别对应各个变量的方差,而第 i 行 j 列和 j 行 i 列元素相同,表示 i 和 j 两个变量的协方差。
2.4 矩阵对角化:根据我们的优化条件,我们需要将除对角线外的其它元素化为 0,并且在对角线上将元素按大小从上到下排列(变量方差尽可能大)。设原始数据矩阵 X 对应的协方差矩阵为 C,而 P 是一组基按行组成的矩阵,设 Y=PX,则 Y 为 X 对 P 做基变换后的数据。设 Y 的协方差矩阵为 D,我们推导一下 D 与 C 的关系:
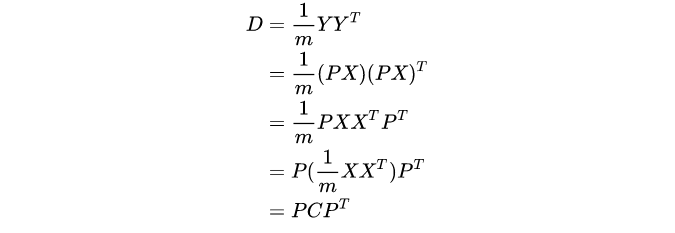
因此,我们要找的 P 是能让原始协方差矩阵对角化的 P。换句话说,优化目标变成了寻找一个矩阵 P,满足 是一个对角矩阵,并且对角元素按从大到小依次排列,那么 P 的前 K 行就是要寻找的基,用 P 的前 K 行组成的矩阵乘以 X 就使得 X 从 N 维降到了 K 维并满足上述优化条件。
至此,我们离 PCA 还有仅一步之遥,我们还需要完成对角化。
原文:https://www.cnblogs.com/meltryllis-melt/p/14411203.html