NumPy(Numerical Python) 是 Python 语言的一个扩展程序库,支持大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库。
- 一个强大的N维数组对象 ndarray
- 广播功能函数
- 整合 C/C++/Fortran 代码的工具
- 线性代数、傅里叶变换、随机数生成等功能
NumPy 最重要的一个特点是其 N 维数组对象 ndarray,它是一系列同类型数据的集合,以 0 下标为开始进行集合中元素的索引。
问题1:Ndarray与array的区别是什么呢?
答:ndarray是一个对象,而array是一个方法(函数),起作用是生成一个ndarry的对象。
问题2:Ndarray是怎么存储的呢?
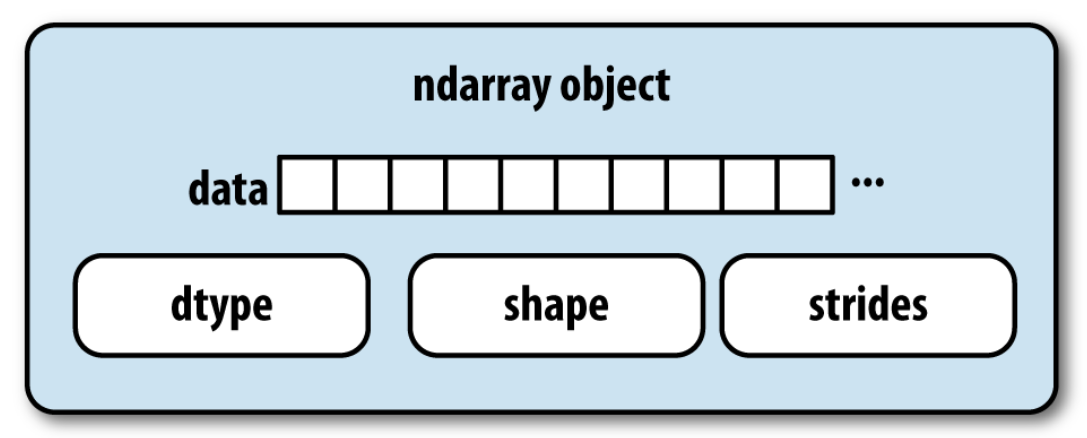
Ndarray具有一下属性:
dtype:表示数组的数据类型
shape:表示数组的维度,或矩阵的秩
strides:暂时不懂·····
# 方式一
matrix = [
[1,2,3,4],
[3,4,5,6],
[7,8,9,10],
[11,12,13,14],
]
matrix = np.array[matrix] #成功
# 方式二
matrix = np.arange(start, end, step) #这样只能创建一维矩阵
matrix = np.arange(star, end, step).reshape(层数, 列数, 行数) #可以通过reshape方法改变
#方法三
matrix = np.zeros(shape, *dtype=None, *order=‘C‘)
matrix = np.ones(shape, *dtype=None, *order=‘C‘)
下面引用知乎@曲奇的例子辅助理解
import numpy as np
# 一维数据不用赘言
data_1d = np.array([0, 1, 2, 3])
# 二维数据作为 m 行 n 列的表格,例如 2 行 3 列
data_2d = np.arange(6).reshape(2, 3)
# 三维数据作为 k 层 m 行 n 列 的积木块, 例如 2 层 3 行 4 列
data_3d = np.arange(24).reshape(2, 3, 4)
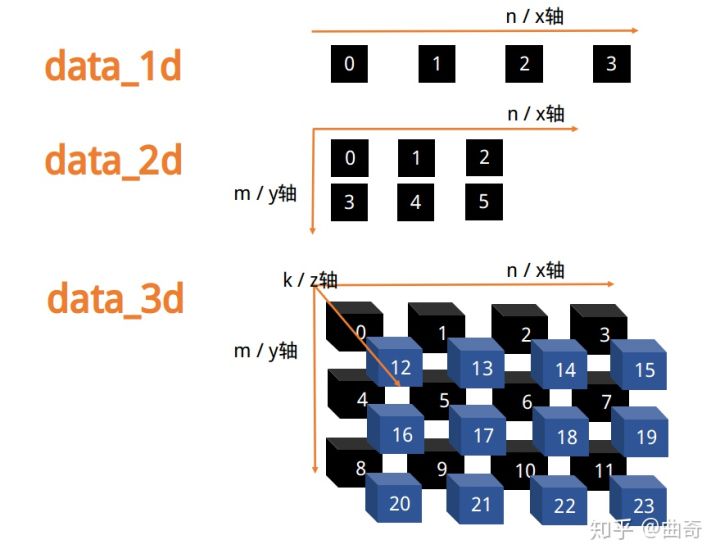
检查一个 ndarray 数据的维度和大小,分别用 ndim 和 shape 属性。
>>> print(data_3d.ndim)
3
>>> print(data_3d.shape)
(2, 3, 4)
shape 是一个很关键的属性,我是这样把它和各个轴对应的:
shape: (2, 3, 4)
k, m, n
z, y, x
心法1: x, y, z 对应的shape元组是从右往左数的。
这是我的个人习惯,也符合主流的用法。
打开一幅 640 x 480 的图像:
import numpy as np
import matplotlib.pylab as plt
image = plt.imread("lena.jpg")
print(image.shape)
# --- 结果 ---
# (480, 640, 3)
# (y, x, c)
不是 640 x 480 吗, 怎么倒过来了?我写代码的时候在这里总是犯迷糊。
在口头表达中,我们先说宽640,再说高480,而在计算机中是先高(y) 后宽(x),注意了!
每个像素有三个颜色分量(color),所以这个维度放在了最右边,可以理解,顺序就是 (y, x, c)
对于4维及更高维度的数据,无法在3维空间图示。这个时候,就不要考虑形象思维了,直接按照规则做处理。
用 shape 属性返回的元组,从左到右,座标轴分别命名为 axis 0, axis 1, ...,请注意,现在是从左向右数,正好是这个元组的 index,在以后的运算中,都按此规定。
>>> print(data.shape)
(3, 3, 2, 5)
# axis 0: 3
# axis 1: 3
# axis 2: 2
# axis 3: 5
心法2: 抽象座标轴顺序从左向右。指定哪个轴,就只在哪个轴向操作,其他轴不受影响。
data = np.array(np.arange(12))
np.random.shuffle(data)
data = data.reshape(3, 4)
print(data)
# [[10 8 3 2]
# [ 5 6 0 7]
# [11 4 9 1]]
print( np.sort(data, axis=0) )
# [[ 5 4 0 1] | 小
# [10 6 3 2] | 到
# [11 8 9 7]] | 大
print( np.sort(data, axis=1) )
# 小 到 大
# --------->
# [[ 2 3 8 10]
# [ 0 5 6 7]
# [ 1 4 9 11]]
如果你在心中能把抽象轴和 x, y, z 对应起来,则理解轴向排序很容易。
shape: (3, 4)
axis: 0, 1
AXIS: y, x
这几个函数调用,一般会指定轴向,注意适用 心法2
sum,mean,std,var,min,max 会导致这个轴被压扁,缩减为一个数值,降维打击??
data = np.arange(24).reshape(2, 3, 4)
print(data)
# [[[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]]
#
# [[12 13 14 15]
# [16 17 18 19]
# [20 21 22 23]]]
print( np.sum(data, axis=0) )
# 0轴被sum压扁,1轴2轴不变
# [[12 14 16 18]
# [20 22 24 26]
# [28 30 32 34]]
print( np.sum(data, axis=1) )
# 1轴被sum压扁,0轴2轴不变
# [[12 15 18 21]
# [48 51 54 57]]
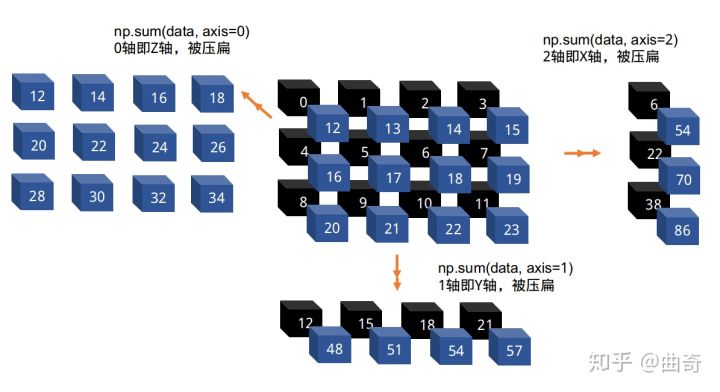
cumsum,cumprod 不缩减轴向,只在指定轴向操作,请读者自己试验。
心法3: 在索引中出现冒号(??,则本轴继续存在,如果只是一个数值,则本轴消失。
例如,像 :, :1, 1: 这样的索引,保留此轴, data[:, :1, 2:] 中,三个轴都保留。 data[1, 4, 2] 三个轴都消失,只返回一个数值。
data[1:2, 0:1, 0:1] 中,三个轴都保留,但只有一个数据元素,很神奇吧。
data = np.arange(24).reshape(2, 3, 4)
print( data )
# [[[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]]
#
# [[12 13 14 15]
# [16 17 18 19]
# [20 21 22 23]]]
print( data[0, :, :] )
# axis 0,即 z 轴,是数值,则 z 轴消失,切了一片 x-y
# [[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]]
print( data[0, 1, 2] )
# 所有轴都消失,只返回一个标量数据
# 6
print( data[0:1, 1:2, 2:3] )
# 返回三维数据,虽然只有一个元素
# [[[6]]]
如何查看 ndarray 的维度呢?可以访问 shape 属性;如果打印出来了,那么就数一数起始的中括号个数,比如 [[[6]]], 有三个 [,那么就是三维数组。你记住了吗?
同样遵循心法2,指定哪个轴,就在哪个轴向拼接:
data = np.arange(4).reshape(2, 2)
print( np.concatenate([data, data], axis=0) )
# 在轴向 0 拼接,即 y 方向
# [[0 1]
# [2 3]
# [0 1]
# [2 3]]
print( np.concatenate([data, data], axis=1) )
# 在轴向 1 拼接,即 x 方向
# [[0 1 0 1]
# [2 3 2 3]]
你有没有这个困惑:在 reshape 之后,数据在各个轴上是如何重新分配的?
搞清楚 ndarray 的数据在内存里的存放方式,以及各个维度的访问方式,reshape 困惑就迎刃而解了。
心法4: ndarray 的数据在内存里以一维线性存放,reshape 之后,数据并没有移动,只是访问方式变了而已。
数据优先填充 X 轴向,其次 Y 轴,其次 Z 轴 。。。
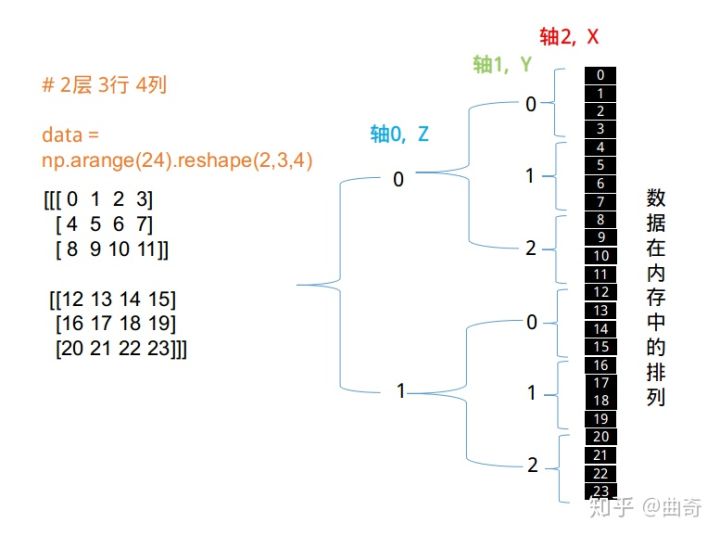
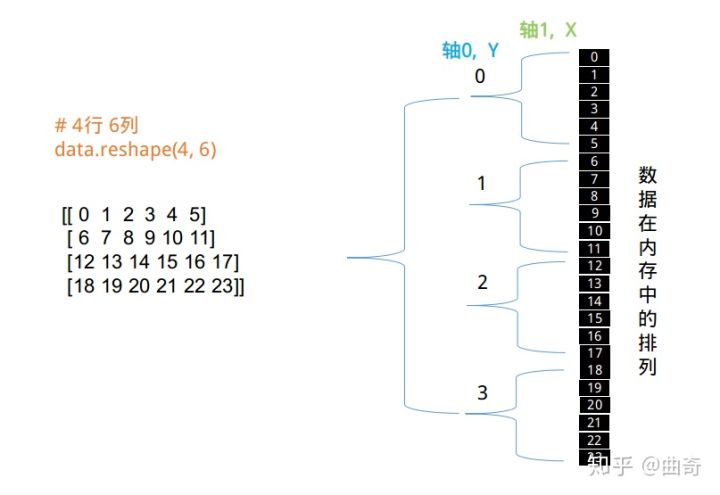
有 C 语言基础的,很容易理解 ndarray 的实现,就是 C 中的多维数组而已。
int data[2][3][4];
int data[4][6];
就说这么多,看了本文请亲自动手写代码体验一下。掌握此心法,可以纵横 numpy 世界而无大碍。
心法1: x, y, z 对应的shape元组是从右往左数的。
心法2: 抽象座标轴顺序从左向右。指定哪个轴,就只在哪个轴向操作,其他轴不受影响。
心法3: 在索引中出现冒号(??,则结果中本轴继续存在,如果只是一个数值,则本轴消失。
心法4: ndarray 的数据在内存里以一维线性存放,reshape 之后,数据并没有移动,只是访问方式变了而已。
1、np.poly1d()此函数有两个参数:
参数1:为一个数组,若没有参数2,则生成一个多项式,例如:
p = np.poly1d([2,3,5,7])
print(p) ==>> 2x^3 + 3x^2 + 5^x + 7 数组中的数值为coefficient(系数),从后往前 0,1,2.。。为位置的次数
参数2:若参数2为True,则表示把数组中的值作为根,然后反推多项式,例如:
q = np.poly1d([2,3,5],True)
print(q) ==>> (x - 2)*(x - 3)*(x - 5) = x^3 - 10x^2 + 31x -30
参数3:variable=‘z’表示改变未知数的字母,例如:
q = np.poly1d([2,3,5],True,varibale = ‘z‘)
print(q) ==>> (z - 2)*(z - 3)*(z - 5) = z^3 - 10z^2 + 31z -30
2、多项式poly1d()的方法
# a. p(0.5)表示当x = 0.5时,多项式的值为多少
b. p.r表示当多项式为 0 时,此等式的根
c. p.c表示生成多项式的系数数组
d. p.order表示返回最高项的次方数
e. p[1]表示返回第一项的系数
f. 多项式支持实数的四则运算
3、 其他函数
a. deriv([m])表示求导,参数m表示求几次导数
b. integ([m,k])表示积分,参数m表示积几次分,k表示积分后的常数项的值
通过
Ndarray的介绍可以知道一维矩阵:有n行、1列,可以用shap[0]验证
二维矩阵:有n行、n列,可以用shape[0] => row, shape[1] => colum
1. flipud()
Flip array in the up/down direction.也就是说进行`行对换`
Equivalent to ``m[::-1,...]``.
Does not require the array to be two-dimensional.# 不需要二维数组
Examples
--------
>>> A = np.diag([1.0, 2, 3])
>>> A
array([[1., 0., 0.],
[0., 2., 0.],
[0., 0., 3.]])
>>> np.flipud(A)
array([[0., 0., 3.],
[0., 2., 0.],
[1., 0., 0.]])
2. fliplr()
Flip array in the left/right direction.也就是说进行`列对换`
Equivalent to m[:,::-1]. Requires the array to be at least 2-D(二维).
Examples
--------
>>> A = np.diag([1.,2.,3.])
>>> A
array([[1., 0., 0.],
[0., 2., 0.],
[0., 0., 3.]])
>>> np.fliplr(A)
array([[0., 0., 1.],
[0., 2., 0.],
[3., 0., 0.]])
3. flip()
Reverse the order of elements in an array along the given axis.
The shape of the array is preserved, but the elements are reordered.
***********************************************************************************
flip(m, 0) is equivalent to flipud(m).
flip(m, 1) is equivalent to fliplr(m).
flip(m, n) corresponds to ``m[...,::-1,...]`` with ``::-1`` at position n.
flip(m) corresponds to ``m[::-1,::-1,...,::-1]`` with ``::-1`` at all
positions.
flip(m, (0, 1)) corresponds to ``m[::-1,::-1,...]`` with ``::-1`` at
position 0 and position 1.
***********************************************************************************
>>> A = np.arange(8).reshape((2,2,2))
>>> A
array([[[0, 1],
[2, 3]],
[[4, 5],
[6, 7]]])
>>> np.flip(A, 0)
array([[[4, 5],
[6, 7]],
[[0, 1],
[2, 3]]])
>>> np.flip(A, 1)
array([[[2, 3],
[0, 1]],
[[6, 7],
[4, 5]]])
>>> np.flip(A)
array([[[7, 6],
[5, 4]],
[[3, 2],
[1, 0]]])
>>> np.flip(A, (0, 2))
array([[[5, 4],
[7, 6]],
[[1, 0],
[3, 2]]])
>>> A = np.random.randn(3,4,5)
>>> np.all(np.flip(A,2) == A[:,:,::-1,...])
True
"""
原文:https://www.cnblogs.com/suyifan/p/14423741.html