树状数组

先从最简单的开始：
一个数组，需要高效查询区间和。如果这个数组的值不变的话，那么只需要弄个前缀和就可以了。

sum[0] = arr[0];
for( int i=1;i<arr.size(); i++){
    sum[i] = sum[i-1] + arr[i];
}
// query i~j
auto ret = sum[j]-sum[i];

如果这个数组值会变的话，那么就要用到树状数组了。因为树状数组可以满足 修改时O(log(n))，查询时O(log(n))。
一般来讲，一个数组里面的值，要么是实际数字，要么是前缀和，都只是一个“意义”
而树状数组，它不一样。它的值是，从这个到那个的区间和。为了高效（满足修改时O(log(n))，查询时O(log(n))）
区间的选择如图（下图来自互联网，侵删）

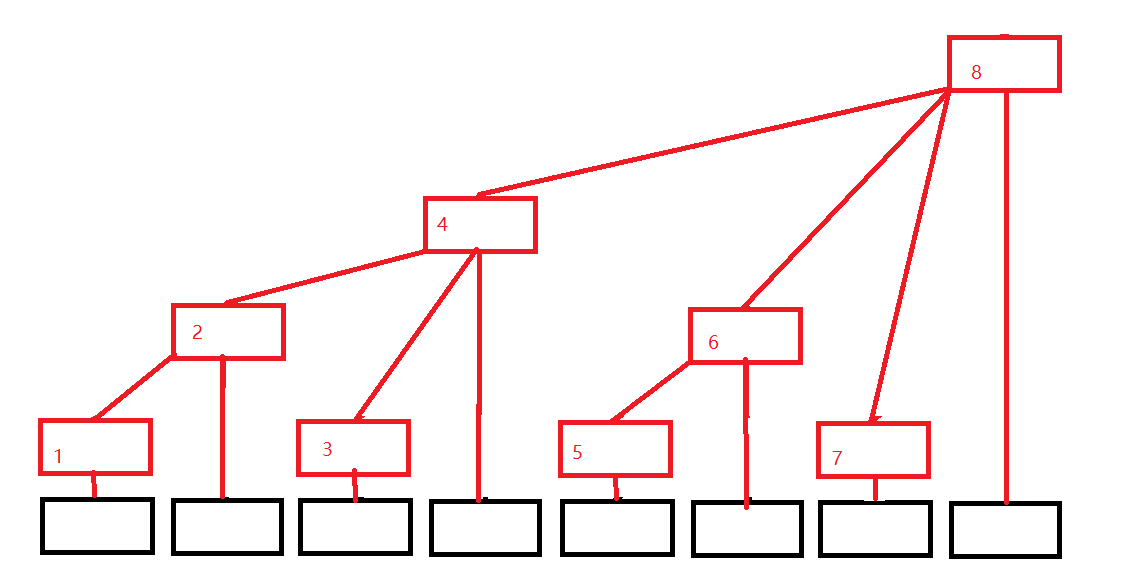
为什么要这样选择，那是刚好理论（数据上）跟实际（代码高效）很好地结合在一起了。
这个时候，
如果我要修改 原始数组 arr[1] 的值，那么实际上在树状数组中，要修改 1,2,4,8 的值
如果要查询 原始数组arr[1~6]的前缀和，那么在树状数组中就是查询 6,4 的值。
所以，引出三段代码

int lowbit(int x) { return x&-x;}
int add(vector<int>&tArr,int idx,int val){
    int len = tArr.size();
    for( int i=idx;i<len;i+=lowbit(i)) tArr[i] += val;
}
int getSum(vector<int> &tArr,int idx){
    int ret = 0;
    for( int i=idx;i>0;i-=lowbit(i)) ret+=tArr[i];
    return ret;
}

以上就是树状数组最原始的应用了。单点更新，区间查询
此外，还有 区间更新，单点查询 与 区间更新，区间查询

区间更新，单点查询

设数组d[i] = arr[i]-arr[i-1] 作为树状态数组的原始数组。
这样，单点查询即为求和。
区间更新，l~r 增加 x;
则只需要 d[l] 值增加x d[r+1] 值减x 即可。

区间更新，区间查询

依然 设数组d[i] = arr[i]-arr[i-1]
前置和


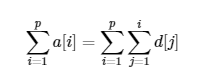
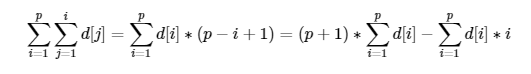
所以，增加多一个数组
sum1[i]=d[i]，sum2[i]=d[i]?i 。
查询:

long long getsum(vector<long long> &arr,vector<long long> &arr2,long long idx){
	long long ans = 0;
	for(int i=idx;i>0;i-=lowbit(i)){
		ans += ((idx+1) * arr[i] - arr2[i]);
	}
	return ans;
}

更新:

void add(vector<long long> &arr,vector<long long>&arr2,long long idx,long long val){
	int len = arr.size();
	for( int i=idx;i<len;i+=lowbit(i) ){
		arr[i] += val;
		arr2[i] +=idx*val;
	}
}

到此就全部介绍完了，附poj3468的代码。
AC代码如下

long long lowbit(long long x)
{
    return x & (-x);
}

void add(vector<long long> &arr, vector<long long>&arr2, long long idx, long long val)
{
    int len = arr.size();
    for (int i = idx; i < len; i += lowbit(i))
    {
        arr[i] += val;
        arr2[i] += idx * val;
    }
}

void add_range(vector<long long> &arr, vector<long long> &arr2, long long a, long long b, long long c)
{
    add(arr, arr2, a, c);
    add(arr, arr2, b + 1, -c);
}

long long getsum(vector<long long> &arr, vector<long long> &arr2, long long idx)
{
    long long ans = 0;
    for (int i = idx; i > 0; i -= lowbit(i))
    {
        ans += ((idx + 1) * arr[i] - arr2[i]);
    }
    return ans;
}

int main()
{
    long long N, Q;
    cin >> N >> Q;
    long long t;
    vector < long long> arr(N + 1, 0);
    vector < long long> arr2(N + 1, 0);
    long long pv = 0;
    for (int i = 0; i < N; i++)
    {
        cin >> t;
        add(arr, arr2, i + 1, t - pv);
        pv = t;
    }
    char Ch;
    long long a, b, c;
    for (int i = 0; i < Q; i++)
    {
        cin >> Ch;
        if (Ch == ‘C‘)
        {
            cin >> a >> b >> c;
            add_range(arr, arr2, a, b, c);
        }
        else
        {
            cin >> a >> b;
            long long r = getsum(arr, arr2, b);
            long long l = getsum(arr, arr2, a - 1);
            cout << r - l << endl;
        }
    }
    return 0;
}

树状数组

原文：https://www.cnblogs.com/kingbuffalo/p/14432660.html