1110 Complete Binary Tree (25 分)

题意

给定一棵二叉树，判断其是否为完全二叉树。如果是的话，同时输出该完全二叉树的最后一个结点编号；否则输出二叉树的根结点编号。

我的思路：
先判断最后一层上面的层是否是满的，最后判断最后一层的结点是否都在最左边。

注意点

一定要注意节点编号可能是两位数，不能用char类型存储。

const int N=25;
PII tree[N];
int fa[N];
int dep[N];
vector<int> last;
int lastnode;
int n;
int d;

int get(string s)
{
    if(s == "-") return -1;
    return stoi(s);
}

bool bfs(int root)
{
    queue<int> q;
    q.push(root);
    dep[root]=1;

    while(q.size())
    {
        int t=q.front();
        q.pop();

        lastnode=t;
        if(dep[t] == d) last.pb(t);

        if(~tree[t].fi)
        {
            dep[tree[t].fi]=dep[t]+1;
            q.push(tree[t].fi);
        }
        else if(dep[t] < d)
            return false;

        if(~tree[t].se)
        {
            dep[tree[t].se]=dep[t]+1;
            q.push(tree[t].se);
        }
        else if(dep[t] < d)
            return false;
    }
    return true;
}

int main()
{
    cin>>n;
    
    for(int i=0;i<n;i++)
    {
        string a,b;
        cin>>a>>b;
        int ta=get(a),tb=get(b);
        tree[i]={ta,tb};
        if(~ta) fa[ta]=i;
        if(~tb) fa[tb]=i;
    }

    int root=0;
    while(fa[root] != 0)
        root=fa[root];
        
    d=log2(n+1);
    
    bool ok=bfs(root);

    if(ok)
    {
        int cnt=(1<<d)-1;
        for(int i=0;i<last.size();i++)
        {
            int k=last[i];
            if(~tree[k].fi) cnt++;
            else if(cnt < n)
            {
                ok=false;
                break;
            }

            if(~tree[k].se) cnt++;
            else if(cnt < n)
            {
                ok=false;
                break;
            }
        }
    }

    if(ok) cout<<"YES"<<‘ ‘<<lastnode<<endl;
    else cout<<"NO"<<‘ ‘<<root<<endl;

    
    //system("pause");
    return 0;
}

晴神的思路：

1. 按题目要求输入所有结点，并赋值其左右孩子。
2. 获得二叉树的根结点编号，即0 ~ (N-1)中未在输入中出现过的那个数。
3. 接下来判断二叉树是否是完全二叉树。
4. 以Sample Two的图为例，如果把空结点也标到图中的话，可以形成下面的二叉树，其中虚线和小结表示实际不存在的空结点。

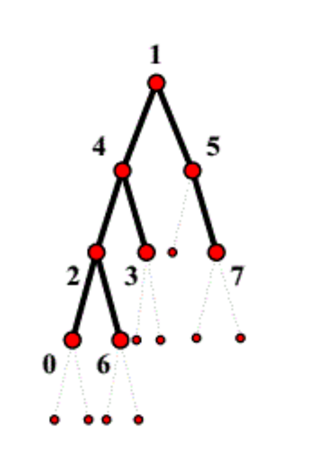
可以发现，如果按照层次遍历的顺序，并且让空结点也在整个过程中被遍历的话，那么在遍历完1->4->5->2->3之后，接下来就会碰到一个空结点，在这个空结点之后才继续遍历完剩余的所有结点，即7->0->6。可以注意到，在这种遍历过程中，在访问完N个非空结点之前就已经碰到了非空结点，因此一定不是完全二叉树，因为对完全二叉树来说，只有当访问完所有N个非空结点之后才会访问到非空结点。

由此可以得到完全二叉树的判断方法，即进行层次遍历，并且让空结点也入队，如果在访问完N个非空结点之前访问到了空结点，那么说明不是完全二叉树。与此同时可以让一个变量last代表二叉树的最后一个结点的编号，不断将其赋值为最后访问到的非空结点即可。

const int N=25;
PII tree[N];
int fa[N];
int lastnode;
int n;

int get(string s)
{
    if(s == "-") return -1;
    return stoi(s);
}

bool bfs(int root)
{
    queue<int> q;
    q.push(root);

    int cnt=0;
    while(q.size())
    {
        int t=q.front();
        q.pop();

        if(~t)
        {
            cnt++;
            lastnode=t;
            q.push(tree[t].fi);
            q.push(tree[t].se);
        }
        else if(cnt < n)
            return false;
    }
    return true;
}

int main()
{
    cin>>n;

    for(int i=0;i<n;i++)
    {
        string a,b;
        cin>>a>>b;
        int ta=get(a),tb=get(b);
        tree[i]={ta,tb};
        if(~ta) fa[ta]=i;
        if(~tb) fa[tb]=i;
    }

    int root=0;
    while(fa[root] != 0)
        root=fa[root];

    bool ok=bfs(root);

    if(ok) cout<<"YES"<<‘ ‘<<lastnode<<endl;
    else cout<<"NO"<<‘ ‘<<root<<endl;


    //system("pause");
    return 0;
}

1110 Complete Binary Tree (25 分)

原文：https://www.cnblogs.com/fxh0707/p/14450607.html