slam十四讲（一）三维空间刚体运动

向量 

• 向量内积

• 向量外积

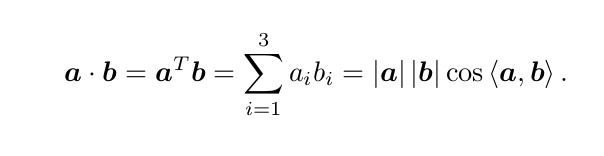
外积的方向垂直于这两个向量,大小为 |a| |b| sin ?a, b?,是两个向量张成的四边形的有向面积。且外积可以表达旋转矩阵。

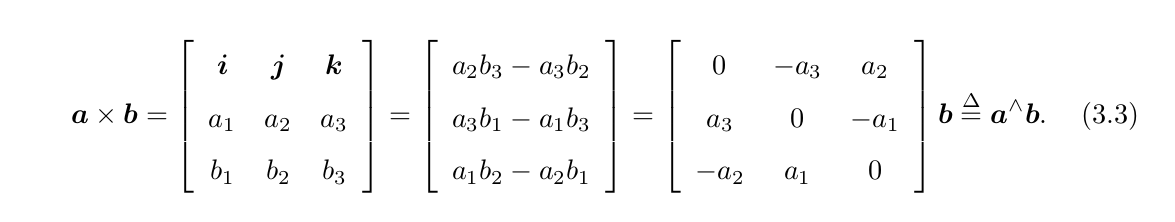
其中这个为反对称矩阵，写作a^

• 旋转矩阵R

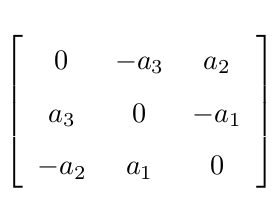
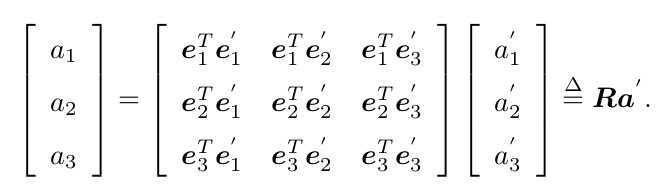
　　我们把中间的阵拿出来,定义成一个矩阵 R。这个矩阵由两组基之间的内积组成,刻画了旋转前后同一个向量的坐标变换关系。只要旋转是一样的,那么这个矩阵也是一样的。

可以说,矩阵 R 描述了旋转本身。因此它又称为旋转矩阵。

　　旋转矩阵的性质：

　　1.R^T=R^-1

　　2.行列式=1

　　3.符合SO(3)性质

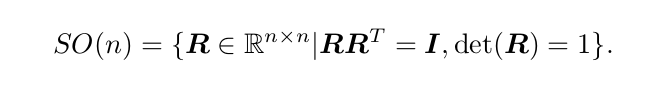
转和平移合到一起,有:
a^、 = Ra + t.

齐次坐标与变化矩阵

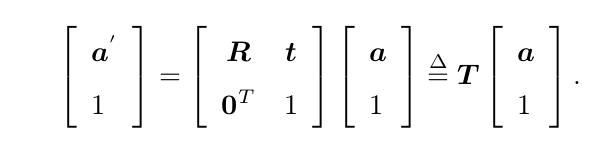
 我们把一个三维向量的末尾添加 1,变成了四维向量,称为齐次坐标。对于这个四维向量,我们可以把旋转和平移写在一个矩阵里面,使得整个关系变成了线性关系。该式中,矩阵 T 称为变换矩阵(Transform Matrix)。我们暂时用 ? 表

示 a 的齐次坐标。

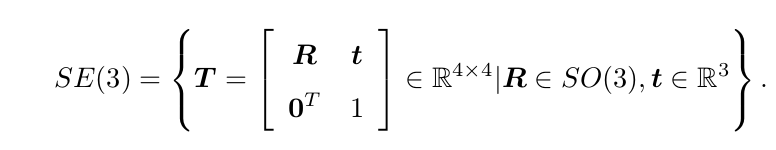
关于变换矩阵 T ,它具有比较特别的结构:左上角为旋转矩阵,右侧为平移向量,左
下角为 0 向量,右下角为 1。这种矩阵又称为特殊欧氏群(Special Euclidean Group):

旋转向量和欧拉角

对于坐标系的旋转,我们知道,任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是,我们可以使用一个
向量,其方向与旋转轴一致,而长度等于旋转角。这种向量,称为旋转向量(或轴角, Axis-Angle)。这种表示法只需一个三维向量即可描述旋转。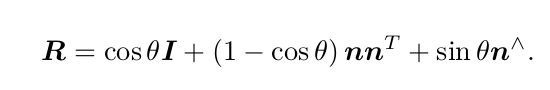

我们也可以计算从一个旋转矩
阵到旋转向量的转换。对于转角 θ,有

• 欧拉角 

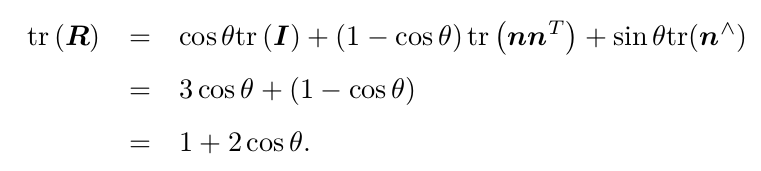
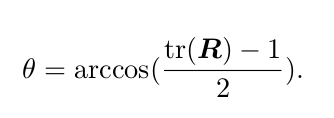
欧拉角则提供了一种非常直观的方式来描述旋转——它使用了三个分离的转角,把一个旋转分解成三次绕不同轴的旋转。

1. 绕物体的 Z 轴旋转,得到偏航角 yaw;
2. 绕旋转之后的 Y 轴旋转,得到俯仰角 pitch;
3. 绕旋转之后的 X 轴旋转,得到滚转角 roll。

• 四元数

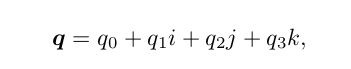
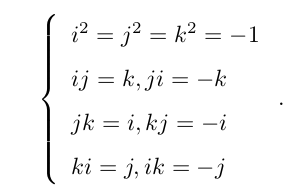
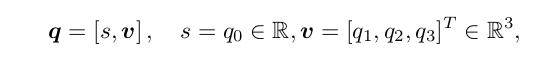
s 称为四元数的实部,而 v 称为它的虚部。如果一个四元数虚部为 0,称之为实四元数。反之,若它的实部为 0,称之为虚四元数。

• 四元数运算

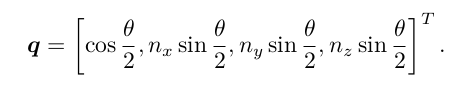
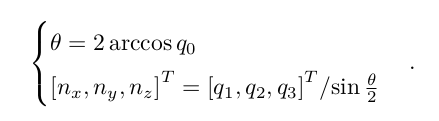
用四元数表示旋转

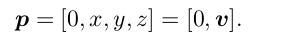
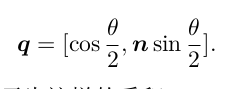
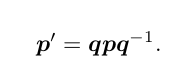
相似、仿射、射影变换

相似变换：

仿射变换：

 射影变换：

slam十四讲（一）三维空间刚体运动

原文：https://www.cnblogs.com/xkbl-blogs/p/14451358.html