ORB(Oriented FAST and BRIEF) 特征是 SLAM 中一种很常用的特征,由于其二进制特性,使得它 可以非常快速地提取与计算 [1]。下面,你将按照本题的指导,自行书写 ORB 的提取、描述子的计算以及 匹配的代码。代码框架参照 computeORB.cpp 文件,图像见 1.png 文件和 2.png。
ORB 即 Oriented FAST 简称。它实际上是 FAST 特征再加上一个旋转量。本习题将使用 OpenCV 自 带的 FAST 提取算法,但是你要完成旋转部分的计算。旋转的计算过程描述如下 [2]:
? 在一个小图像块中,先计算质心。质心是指以图像块灰度值作为权重的中心。
在一个小的图像块 B 中,定义图像块的矩为:
? \(m_{pq} = \sum_{x,y \in B} x^py^qI(x,y), p,q = \{0,1\}\)
通过矩可以找到图像块的质心:
? \(C=(\frac{m_{10}}{m_{00}},\frac{m_{01}}{m_{00}})\)
连接图像块的几何中心 O 与质心 C,得到一个方向向量 \(\overrightarrow{OC}\),于是特征点的方向可以定义为:
? \(\theta = \arctan(m_{01}/m_{10})\)
实际上只需计算 \(m_{01}\) 和 \(m_{10}\) 即可。习题中取图像块大小为 16x16,即对于任意点 (u,v),图像块从 (u?8,v?8) 取到 (u + 7,v + 7) 即可。请在习题的 computeAngle 中,为所有特征点计算这个旋转角。
提示:
由于要取图像 16x16 块,所以位于边缘处的点(比如 u < 8 的)对应的图像块可能会出界,此时 需要判断该点是否在边缘处,并跳过这些点。
由于矩的定义方式,在画图特征点之后,角度看起来总是指向图像中更亮的地方。
std::atan 和 std::atan2 会返回弧度制的旋转角,但 OpenCV 中使用角度制,如使用 std::atan 类 函数,请转换一下。 作为验证,第一个图像的特征点如图 1 所示。看不清可以放大看。
// compute the angle
void computeAngle(const cv::Mat &image, vector<cv::KeyPoint> &keypoints) {
int half_patch_size = 8;
for (auto &kp : keypoints) {
// START YOUR CODE HERE (~7 lines)
kp.angle = 0; // compute kp.angle
int u = kp.pt.x;
int v = kp.pt.y; //height y => image row
if( u - 8 >= 0 && u + 7 <= image.cols && v - 8 >= 0 && v + 7 <= image.rows){ // vaild keypoint
int m01 = 0;
int m10 = 0;
// (row, col) <=> (h,w) <=> (v,u)
for(int j = -8; j < 8; j++){
for(int i = -8; i < 8; i++){
m01 += j*image.at<uchar>(v + j, u + i); // y*Iuv
m10 += i*image.at<uchar>(v + j, u + i); // x*Iuv
}
}
kp.angle = (float)atan2(m01, m10)*180/pi;
}
// END YOUR CODE HERE
}
return;
}

ORB 描述即带旋转的 BRIEF 描述。所谓 BRIEF 描述是指一个 0-1 组成的字符串(可以取 256 位或 128 位),每一个 bit 表示一次像素间的比较。算法流程如下:
给定图像 I 和关键点 (u,v),以及该点的转角 θ。以 256 位描述为例,那么最终描述子
? \(d=[d_1, d_2, \cdots, d_{256}]\)
对任意 i = 1,...,256,\(d_i\) 的计算如下。取 (u,v) 附近任意两个点 p,q,并按照 θ 进行旋转:
? \(\begin{bmatrix} u_p‘\\ v_p‘ \end{bmatrix}= \begin{bmatrix} \cos \theta & -\sin\theta\\ \sin\theta & \cos \theta \end{bmatrix} \begin{bmatrix} u_p\\ v_p \end{bmatrix}\)
其中 \(u_p,v_p\) 为 \(p\) 的坐标,对 \(q\) 亦然。记旋转后的 \(p,q\) 为 \(p′,q′\),那么比较 \(I(p′)\) 和 \(I(q′)\),若前者大,记 \(di = 0\) ,反之记 \(d_i = 1^1\)。
这样我们就得到了 ORB 的描述。我们在程序中用 256 个 bool 变量表达这个描述2。请你完成 computeORBDesc 函数,实现此处计算。注意,通常我们会固定 p,q 的取法(称为 ORB 的 pattern),否则每 次都重新随机选取,会使得描述不稳定。我们在全局变量 ORB_pattern 中定义了 p,q 的取法,格式为 up,vp,uq,vq。请你根据给定的 pattern 完成 ORB 描述的计算。
提示:
p,q 同样要做边界检查,否则会跑出图像外。如果跑出图像外,就设这个描述子为空。
调用 cos 和 sin 时同样请注意弧度和角度的转换。
// START YOUR CODE HERE (~7 lines)
d[i] = 0; // if kp goes outside, set d.clear()
int pattern[4], pattern_R[4]; // up, vp, uq, vq;
for(int j = 0; j < 4; j++){
pattern[j] = ORB_pattern[i*4 + j];
}
// rotation
pattern_R[0] = pattern[0]*cos(kp.angle/180*pi) - pattern[1]*sin(kp.angle/180*pi);
pattern_R[1] = pattern[0]*sin(kp.angle/180*pi) + pattern[1]*cos(kp.angle/180*pi);
pattern_R[2] = pattern[2]*cos(kp.angle/180*pi) - pattern[3]*sin(kp.angle/180*pi);
pattern_R[3] = pattern[2]*sin(kp.angle/180*pi) + pattern[3]*cos(kp.angle/180*pi);
// point
pattern_R[0] += kp.pt.x;
pattern_R[1] += kp.pt.y;
pattern_R[2] += kp.pt.x;
pattern_R[3] += kp.pt.y;
if(pattern_R[0] < 0 || pattern_R[0] >= image.cols || pattern_R[1] < 0 || pattern_R[1] >= image.rows
|| pattern_R[2] < 0 || pattern_R[2] >= image.cols || pattern_R[3] < 0 || pattern_R[3] >= image.rows){
d.clear();
break;
}else{
d[i] = (image.at<uchar>(pattern_R[1], pattern_R[0]) > image.at<uchar>(pattern_R[3], pattern_R[2])) ? 0 : 1;
}
// END YOUR CODE HERE
在提取描述之后,我们需要根据描述子进行匹配。暴力匹配是一种简单粗暴的匹配方法,在特征点不多时很有用。下面你将根据习题指导,书写暴力匹配算法。
所谓暴力匹配思路很简单。给定两组描述子 \(P = [p_1,...,p_M]\) 和 \(Q = [q_1,...,q_N]\)。那么,对 \(P\) 中任意一个点,找到 \(Q\) 中对应最小距离点,即算一次匹配。但是这样做会对每个特征点都找到一个匹配,所以我们通常还会限制一个距离阈值 \(d_{max}\),即认作匹配的特征点距离不应该大于 \(d_{max}\)。下面请你根据上述描述,实现函数 bfMatch,返回给定特征点的匹配情况。实践中取 \(d_{max} = 50\)。
提示:
你需要按位计算两个描述子之间的汉明距离。
OpenCV 的 DMatch 结构,queryIdx 为第一图的特征 ID,trainIdx 为第二个图的特征 ID。
作为验证,匹配之后输出图像应如图 2 所示。
// find matches between desc1 and desc2.
int d1_id = -1;
for(auto &d1: desc1){
d1_id++;
if(!d1.empty()){
vector<vector<int> > d1_match(0, vector<int>(2)); // record [hanmming, d1_id]
int d2_id = -1;
for(auto &d2: desc2){
d2_id++;
if(!d2.empty()){
int hamming = 0;// init
for(int i = 0; i < 256; i++){
hamming += (d1[i] == d2[i]) ? 0 : 1;
}
d1_match.push_back({hamming, d2_id});
}
}
sort(d1_match.begin(), d1_match.end()); //hamming, order lowest to sort
if(d1_match[0][0] < d_max){
cv::DMatch m;
m.queryIdx = d1_id;
m.trainIdx = d1_match[0][1]; //d2_id
m.distance = d1_match[0][0];
matches.push_back(m);
}
}
}
// END YOUR CODE HERE

最后,请结合实验,回答下面几个问题:
为什么说 ORB 是一种二进制特征?
因为其描述子是以二进制表示的
为什么在匹配时使用 50 作为阈值,取更大或更小值会怎么样?
阈值取得过大会导致误匹配率增加;阈值取得过小会导致匹配对过少。这两种情况会导致后续的位姿求解不稳定。
暴力匹配在你的机器上表现如何?你能想到什么减少计算量的匹配方法吗?
在我的机器上秒出,后续可以采用快速最近邻匹配法。
我们在书中讲到了单目对极几何部分,可以通过本质矩阵 E,得到旋转和平移 R,t,但那时直接使用了 OpenCV 提供的函数。本题中,请你根据数学原理,完成从 E 到 R,t 的计算。程序框架见 code/E2Rt.cpp.
设 Essential 矩阵 E 的取值为(与书上实验数值相同):
? \(E=\begin{bmatrix} ?0.0203618550523477 & ?0.4007110038118445 & ?0.03324074249824097\\ 0.3939270778216369 & ?0.03506401846698079 & 0.5857110303721015\\ ?0.006788487241438284 & ?0.5815434272915686 & ?0.01438258684486258 \end{bmatrix}\)
请计算对应的 R,t,流程如下:
对 E 作 SVD 分解:
? \(E=U\sum V^T\)
处理 Σ 的奇异值。设 Σ = diag(σ1,σ2,σ3) 且 σ1 ≥ σ2 ≥ σ3,那么处理后的 Σ 为:
? \(\sum = diag(\frac{\sigma_1 + \sigma_2}{2}, \frac{\sigma_1 + \sigma_2}{2}, 0)\)
共存在四个可能的解:
? \(t^∧_1 = UR_Z(\frac{π}{2})ΣU^T\), \(R_1 = UR^T_Z(\frac{π}{2})V^T\)
? \(t^∧_2 = UR_Z(?\frac{π}{2})ΣU^T\), \(R_2 = UR^T_Z(?\frac{π}{2})V^T.\)
其中 \(R_Z(\frac{π}{2})\) 表示沿 Z 轴旋转 90 度得到的旋转矩阵。同时,由于 ?E 和 E 等价,所以对任意一 个 t 或 R 取负号,也会得到同样的结果。因此,从 E 分解到 t,R 时,一共存在四个可能的解。请 打印这四个可能的 R,t。
提示:用 AngleAxis 或 Sophus::SO3 计算 \(R_Z(\frac{π}{2})\)。
? 注:实际当中,可以利用深度值判断哪个解是真正的解,不过本题不作要求,只需打印四个可能的解 即可。同时,你也可以验证 t∧R 应该与 E 只差一个乘法因子,并且与书上的实验结果亦只差一个乘法因子。
// START YOUR CODE HERE
JacobiSVD<MatrixXd> svd(E, ComputeThinU | ComputeThinV);
Matrix3d U = svd.matrixU();
Matrix3d V = svd.matrixV();
Matrix3d Sigma = U.inverse()*E*V.transpose().inverse();
vector<double> diag = {Sigma(0,0), Sigma(1,1), Sigma(2,2)};
sort(diag.begin(), diag.end());
double tau = (diag[2] + diag[1])*0.5;
Matrix3d Sigma_tau = Matrix3d::Zero();
Sigma_tau(0,0) = tau;
Sigma_tau(1,1) = tau;
Matrix3d R_Z1 = AngleAxisd(M_PI/2, Vector3d(0,0,1)).matrix();
Matrix3d R_Z2 = AngleAxisd(-M_PI/2, Vector3d(0,0,1)).matrix();
// END YOUR CODE HERE
// set t1, t2, R1, R2
// START YOUR CODE HERE
Matrix3d t_wedge1 = U*R_Z1*Sigma_tau*U.transpose(); //t_hat
Matrix3d t_wedge2 = U*R_Z2*Sigma_tau*U.transpose();
Matrix3d R1 = U*R_Z1*V.transpose();
Matrix3d R2 = U*R_Z2*V.transpose();
// END YOUR CODE HERE
运行结果:
kieranych@kieranych-ThinkPad-Edge-E431:~/vslam/hw5/L5/code/E2Rt/build$ ./E2Rt
R1 = -0.998596 0.0516992 -0.0115267
-0.0513961 -0.99836 -0.0252005
0.0128107 0.0245727 -0.999616
R2 = -0.365887 -0.0584576 0.928822
-0.00287462 0.998092 0.0616848
0.930655 -0.0198996 0.365356
t1 = -0.581301
-0.0231206
0.401938
t2 = 0.581301
0.0231206
-0.401938
t^R = 0.0203619 0.400711 0.0332407
-0.393927 0.035064 -0.585711
0.00678849 0.581543 0.0143826
Bundle Adjustment 并不神秘,它仅是一个目标函数为重投影误差的最小二乘。我们演示了 Bundle Adjustment 可以由 Ceres 和 g2o 实现,并可用于 PnP 当中的位姿估计。本题,你需要自己书写一个高斯牛顿法,实现用 Bundle Adjustment 优化位姿的功能,求出相机位姿。严格来说,这是 Bundle Adjustment 的一部分,因为我们仅考虑了位姿,没有考虑点的更新。完整的 BA 需要用到矩阵的稀疏性,我们留到第 七节课介绍。
假设一组点的 3D 坐标为 \(P = {p_i}\),它们在相机中的坐标为 \(U = {u_i}\),\(?i = 1,...n\)。在文件 p3d.txt 和 p2d.txt 中给出了这两组点的值。同时,设待估计的位姿为 T∈SE(3),内参矩阵为:
? \(K=\begin{bmatrix} 520.9 & 0 & 325.1\\ 0& 521.0 & 249.7\\ 0 & 0 & 1 \end{bmatrix}\)
请你根据上述条件,用 G-N 法求出最优位姿,初始估计为 \(T_0 = I\)。程序 GN-BA.cpp 文件提供了大致的 框架,请填写剩下的内容。 在书写程序过程中,回答下列问题:
作为验证,最后估计得到的位姿应该接近:
? \(T^* =\begin{bmatrix} 0.9978 & ?0.0517 & 0.0399 & ?0.1272\\ 0.0506 & 0.9983 &0.0274 & ?0.007\\ ?0.0412 & ?0.0253 & 0.9977 & 0.0617\\ 0& 0 & 0 & 1 \end{bmatrix}\)
这和书中使用 g2o 优化的结果很接近\(^3\)。
int main(int argc, char **argv) {
VecVector2d p2d;
VecVector3d p3d;
Matrix3d K;
double fx = 520.9, fy = 521.0, cx = 325.1, cy = 249.7;
K << fx, 0, cx, 0, fy, cy, 0, 0, 1;
// load points in to p3d and p2d
// START YOUR CODE HERE
ifstream p2d_fin; //(uv)
p2d_fin.open(p2d_file);
string s;
while(getline(p2d_fin, s) && !s.empty()){
istringstream p2d_data(s);
Vector2d p2d_temp;
p2d_data >> p2d_temp[0] >> p2d_temp[1];
p2d.push_back(p2d_temp);
}
p2d_fin.close();
ifstream p3d_fin; //(xyz)
p3d_fin.open(p3d_file);
while(getline(p3d_fin, s) && !s.empty()){
istringstream p3d_data(s);
Vector3d p3d_temp;
p3d_data >> p3d_temp[0] >> p3d_temp[1] >> p3d_temp[2];
p3d.push_back(p3d_temp);
}
p3d_fin.close();
// END YOUR CODE HERE
assert(p3d.size() == p2d.size());
int iterations = 100;
double cost = 0, lastCost = 0;
int nPoints = p3d.size();
cout << "points: " << nPoints << endl;
Sophus::SE3 T_esti; // estimated pose
for (int iter = 0; iter < iterations; iter++) {
Matrix<double, 6, 6> H = Matrix<double, 6, 6>::Zero();
Vector6d b = Vector6d::Zero();
cost = 0;
// compute cost
for (int i = 0; i < nPoints; i++) {
// compute cost for p3d[I] and p2d[I]
// START YOUR CODE HERE
Vector3d p_cam = T_esti*p3d[i];
Vector3d e_3d = Vector3d(p2d[i][0], p2d[i][1], 1) - K*p_cam/p_cam[2]; // (x/z, y/z, 1)
Vector2d e(e_3d[0], e_3d[1]); //e_3d[2] = 0
cost += 0.5*e.transpose()*e; //0.5*e^2
// END YOUR CODE HERE
// compute jacobian
Matrix<double, 2, 6> J;
// START YOUR CODE HERE
double x = p_cam[0], y = p_cam[1], z = p_cam[2];
J(0, 0) = -fx/z;
J(0, 2) = fx*x/(z*z);
J(0, 3) = fx*x*y/(z*z);
J(0, 4) = -fx - fx*(x*x)/(z*z);
J(0, 5) = fx*y/z;
J(1, 1) = -fy/z;
J(1, 2) = fy*y/(z*z);
J(1, 3) = fy + fy*(y*y)/(z*z);
J(1, 4) = -fy*x*y/(z*z);
J(1, 5) = -fy*x/z;
// END YOUR CODE HERE
// J^T J dx = -J^T e
H += J.transpose() * J;
b += -J.transpose() * e;
}
// solve dx
Vector6d dx;
// START YOUR CODE HERE
dx = H.ldlt().solve(b);
// END YOUR CODE HERE
if (isnan(dx[0])) {
cout << "result is nan!" << endl;
break;
}
if (iter > 0 && cost >= lastCost) {
// cost increase, update is not good
cout << "cost: " << cost << ", last cost: " << lastCost << endl;
break;
}
// update your estimation
// START YOUR CODE HERE
T_esti = Sophus::SE3::exp(dx)*T_esti;
// END YOUR CODE HERE
lastCost = cost;
cout << "iteration " << iter << " cost=" << cout.precision(12) << cost << endl;
}
cout << "estimated pose: \n" << T_esti.matrix() << endl;
return 0;
}
运行结果:
kieranych@kieranych-ThinkPad-Edge-E431:~/vslam/hw5/L5/code/GN-BA/build$ ./gn-ba
points: 76
iteration 0 cost=622769.1141257
iteration 1 cost=12206.604278533
iteration 2 cost=12150.675954556
iteration 3 cost=12150.6753269
iteration 4 cost=12150.6753269
cost: 150.6753269, last cost: 150.6753269
estimated pose:
0.997866186837 -0.0516724392948 0.0399128072711 -0.127226621
0.050595918872 0.998339770315 0.0275273682291 -0.00750679765351
-0.0412689491074 -0.0254492048098 0.998823914318 0.061386084881
0 0 0 1
在实际当中,我们经常需要比较两条轨迹之间的误差。第三节课习题中,你已经完成了两条轨迹之间 的 RMSE 误差计算。但是,由于 ground-truth 轨迹与相机轨迹很可能不在一个参考系中,它们得到的轨 迹并不能直接比较。这时,我们可以用 ICP 来计算两条轨迹之间的相对旋转与平移,从而估计出两个参考 系之间的差异。
设真实轨迹为 \(T_g\),估计轨迹为 \(T_e\),二者皆以 \(T_{WC}\) 格式存储。但是真实轨迹的坐标原点定义于外部 某参考系中(取决于真实轨迹的采集方式,如 Vicon 系统可能以某摄像头中心为参考系,见图 3),而估计 轨迹则以相机出发点为参考系(在视觉 SLAM 中很常见)。由于这个原因,理论上的真实轨迹点与估计轨 迹点应满足:
\(T_{g,i} = T_{ge}T_{e,i}\)
其中 i 表示轨迹中的第 i 条记录,\(T_{ge} ∈SE(3)\) 为两个坐标系之间的变换矩阵,该矩阵在整条轨迹中保持 不变。\(T_{ge}\) 可以通过两条轨迹数据估计得到,但方法可能有若干种:
认为初始化时两个坐标系的差异就是 \(T_{ge}\),即:
? \(T_{ge} = T_{g,1}T^{?1}_{e,1}\).
在整条轨迹上利用最小二乘计算 \(T_{ge}\):
? \(T_{ge} = \arg \underset{T_{ge}}{ min} \sum_{i=1}{n}||log(T^{?1}_{gi}T_{ge}T_{e,i})^∨ ||_2\)
把两条轨迹的平移部分看作点集,然后求点集之间的 ICP,得到两组点之间的变换。 其中第三种也是实践中用的最广的一种。现在请你书写 ICP 程序,估计两条轨迹之间的差异。轨迹文 件在 compare.txt 文件中,格式为:
? \(time_e,t_e,q_e,time_g,t_g,q_g,\)
其中 t 表示平移,q 表示单位四元数。请计算两条轨迹之间的变换,然后将它们统一到一个参考系,并画 在 pangolin 中。轨迹的格式与先前相同,即以时间,平移,旋转四元数方式存储。
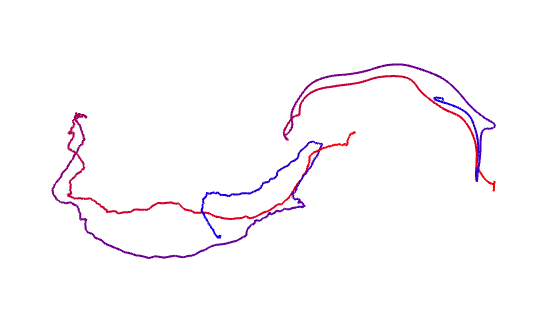
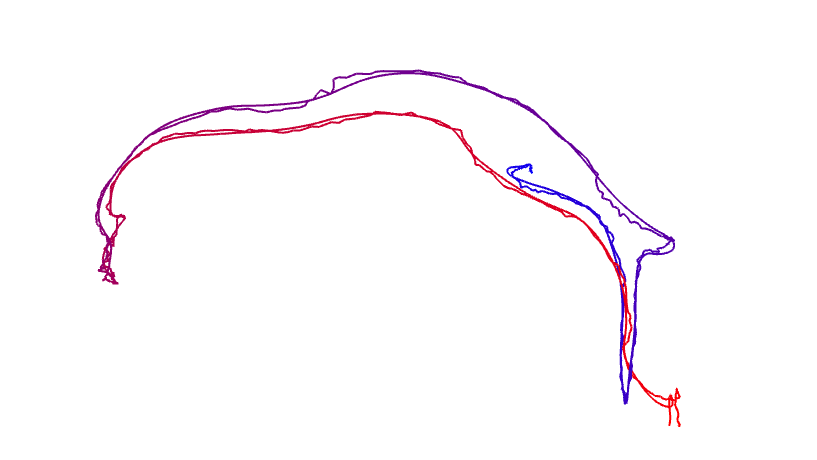
本题不提供代码框架,你可以利用之前的作业完成本题。图 4 显示了对准前与对准后的两条轨迹。
运行结果:
kieranych@kieranych-ThinkPad-Edge-E431:~/vslam/hw5/L5/code/compare/build$ ./draw_gt_est
3d-3d pairs: 612
W= 476.887 31.8495 -128.09
88.5167 -39.3434 34.6791
-3.32456 -8.22012 -1.70694
U= 0.988585 -0.150113 -0.0128977
0.150527 0.987718 0.0418997
-0.0064496 0.0433628 -0.999039
V= 0.968777 0.221248 0.111896
0.051191 -0.620082 0.782865
-0.242592 0.752694 0.612047
ICP via SVD results:
R = 0.923063 0.133592 -0.360706
0.369047 -0.571958 0.732576
-0.108443 -0.809331 -0.577255
t = 1.54022
0.932743
1.44744
(poses_gt, poses_est): RMSE: 3.74174
(poses_gt, poses_est_cor): RMSE: 0.041552
1)坐标系未对齐: RMSE: 3.74174
原文:https://www.cnblogs.com/yujingxiang/p/14459599.html