logistic算法能够对数据进行二分类。
比如我们有两组二维空间数据,最终要求的是一个分类直线,可以设定为计算w(1)+w(2)*x+w(3)*y=0这样的直线。
问题就变为了如何求w的问题。
网上有很多推导,这里就不推导了,不过还是要写几个关键公式。
可以设定logistic函数为:
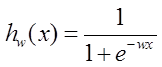
设定损失函数为:
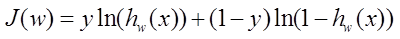
对J中w求导得到迭代方向:
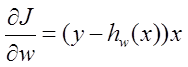
然后不断迭代就行了:
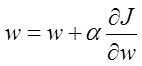
下面代码中y就是data(:,4),即我们的标签项;x就是data(:,1:3)。
matlab程序如下:
clear all;close all;clc; mu1=[0 0]; S1=[0.5 0.1]; data1=mvnrnd(mu1,S1,100); plot(data1(:,1),data1(:,2),‘r.‘); hold on; mu2=[1.5 1.5]; S2=[0.4 0.3]; data2=mvnrnd(mu2,S2,100); plot(data2(:,1),data2(:,2),‘g.‘); data1 = [data1 zeros(length(data1),1)]; data2 = [data2 ones(length(data2),1)]; %两组数据打标签 data = [data1;data2]; %数据组合 data = [ones(length(data),1) data]; %数据第一列增加其次项 w = rand(1,3); alpha = 0.01; for i=1:1000 w = w + alpha*(data(:,4)‘ - 1./(1+exp(-(w*data(:,1:3)‘))))*data(:,1:3); %交叉熵求导迭代 end x = min(data(:,2))-1:0.1:max(data(:,2))+1; y = (-w(1)-w(2)*x)/w(3); plot(x,y,‘b‘);
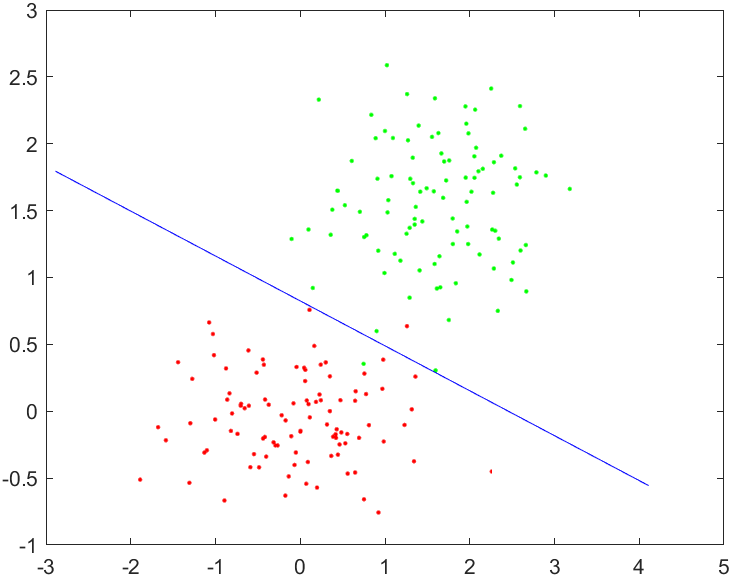
结果如下:
原文:https://www.cnblogs.com/tiandsp/p/14471852.html