内容摘自:数据结构与算法之美
链表并不需要一块连续的内存空间,它通过“指针”将一组零散的内存块串联起来使用。
如图所示
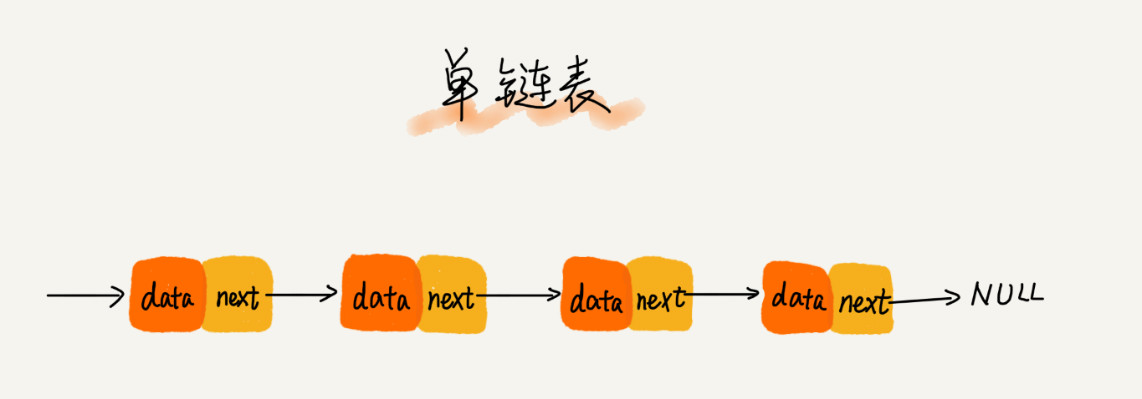
我们习惯把第一个结点叫头结点,把最后一个结点叫尾结点。尾结点指针指向一个空地址NULL。
链表支持数据的查找、插入和删除操作,
插入、删除操作如下图所示。时间复杂度O(1)。
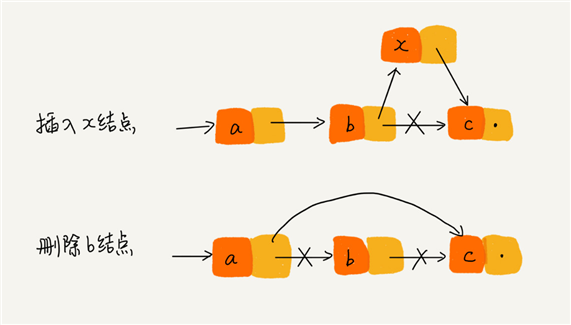
查询操作智能一个一个的往下找,所以随机查询的时间复杂度为O(n)。
循环链表是一种特殊的单链表。循环链表的尾结点指针是指向链表的头结点。
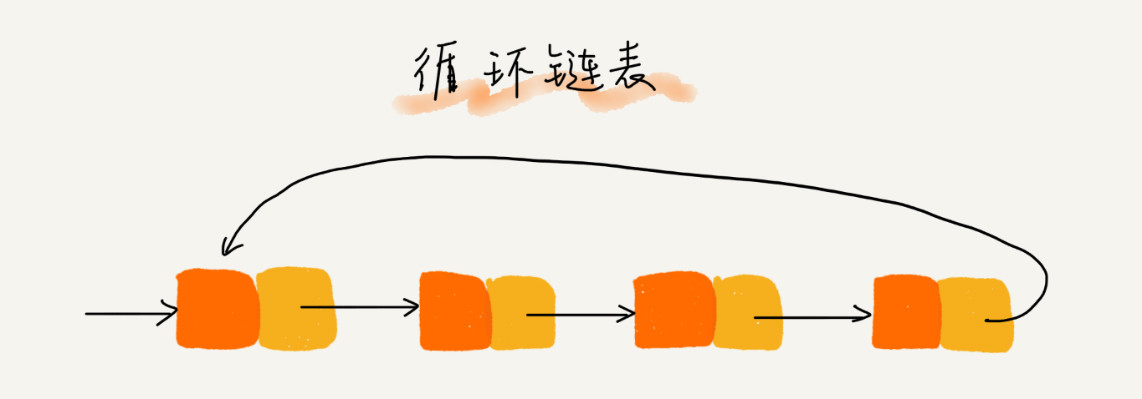
约瑟夫问题就可以用循环链表解决。
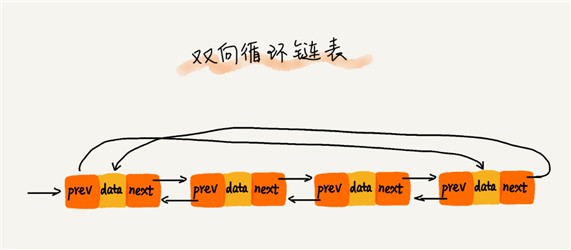
双向链表支持两个方向,每个结点有一个后继指针 next 指向后一个结点,还有一个前驱指针 prev 指向前一个结点。
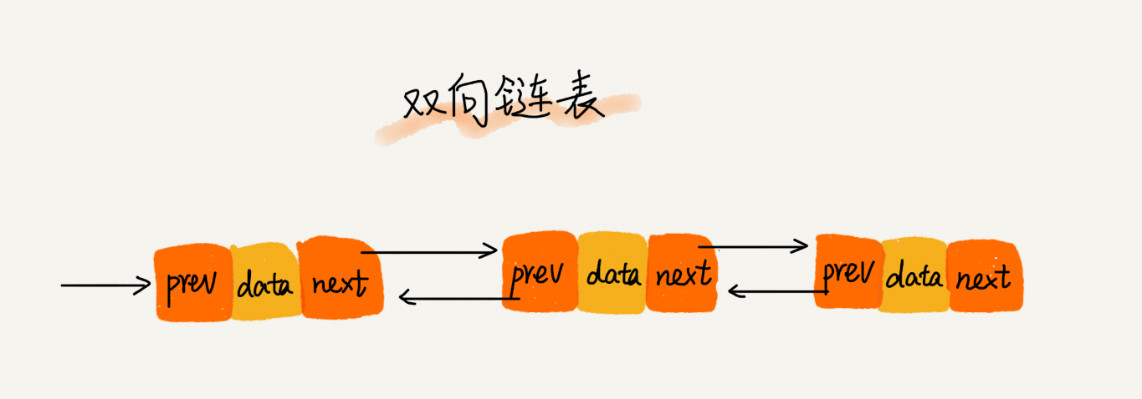
双向链表需要额外的两个空间存储 next 和 prev 结点的地址。因此,存储数据一定的情况下,双向链表会占用更多的内存空间。
从结构上看,prev 结点指针存放的是前驱结点的地址,因此双向链表的查询的时间复杂度为 O(1),即可以根据地址找到结点。相对的,插入、删除等操作也要比单链表简单。
删除操作是如何比单链表高效的
实际开发中,从链表中删除一个数据一般就两种情况:
分析思路
第一种情况,单向链表、双向链表都需要依次遍历对比,直到找到该值,再删除。
第二种情况
已经找到了要删除的结点,但是根据删除操作,还需要知道被删除结点的前驱结点。
因此,为了找到前驱结点,单链表还需要进行一次遍历,直到找到p->next=q。但是对于双向链表则不用,因为 prev 已经保存了前驱结点的地址。
对于查询操作
对于一个有序的链表来说,双向链表的按值查询效率也要高一些。
因为对于位置 p,可以根据要查询的值与 p 结点的值之间的大小关系,决定向前查询还是向后查询。
实际开发过程中,要掌握用空间换时间的设计思想。
常见缓存淘汰策略
思路分析
维护一个有序单链表,结点顺序插入,越靠后的是越早之前访问的,越靠前越新。
当一个新数据被访问时,开始遍历链表。
原文:https://www.cnblogs.com/zzfan/p/14491831.html