记一下自己不会的题/想了一段时间的题吧。
这个题的策略类似于“接头”。
首先有一个前置重要观察,就是最多 \(a\) 中只有两个奇数。原因是我们考虑将其转化为图论模型,一个大小为 \(a_i\) 的块会连 \((a_i / 2)\) 下取整条边。假如出现了 3 个以上的奇数那显然就无解了。所以奇数最多为两个。
对于偶数的 \(a_i\),可以利用如下的“内卷模型”:
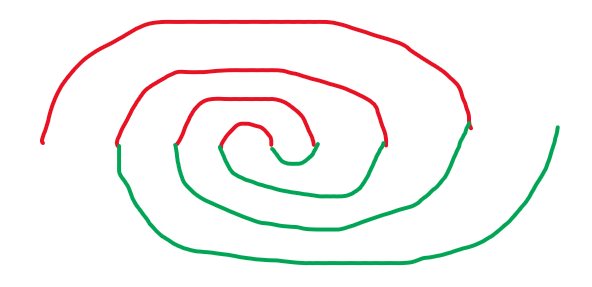
这样就是耗掉一个红色插头,新建一个绿色插头。
也可以“建头”:
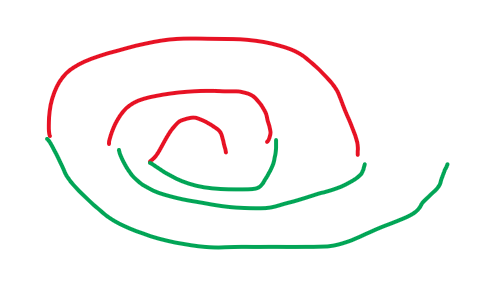
奇数的唯一不同点在于内卷模型没有了,建头模型还有。
那由于最多只有 2 个奇数,那么放到两边之后用建头模型即可(偶数也可以建头模型),中间的偶数用内卷模型。复杂度 \(O(N)\).
首先容易观察到假如 \(a_i + a_{i+1} \geq L\) 对于所有 \(i\) 均成立则一定无解,因为最后一步一定是两个分开。
假如存在,那么可以通过从两边削的方式构造出一组方案,故的解。
Kruskal 重构树板题。
神必博弈论。
我开场以为我会了个 \(n^2 a_i\) 的做法,然后就蒙了。后来发现排个序就是 \(na_i\) 的。
具体来讲,我们令 \(win(i, j)\) 表示当前所有数都被减了 \(i\),且目前 \(j+1...n\) 的 \(a\) 都被删光的情况下,先手是否有必赢策略。
首先判掉 \(i=a_1\) 和 \(j=1\) 的两类情况,接下来假设两种操作都能搞,那么转移到 \(win(i+1, j)\) 和 \(win(i, j-1)\). 然后就自闭了。。。
注意到一个精妙的性质,就是这个东西等价于在一个图上游走,游走到边界的人算输。同时一条对角线上的输赢状态相等,证明如下:
假如 (x, y) 输,那么其左边和下边的点赢,(x-1,y-1) 输。
假如 (x, y) 赢,(x-1, y-1) 赢,那么这一对角线左边和右边的对角线必有一条输,则 (x-2, y-2) 输。
然后就只需要求 \(O(n)\) 个点的 dp 值了。
#include <bits/stdc++.h>
const int N = 1e5 + 5;
int n, A[N];
int main() {
std::ios::sync_with_stdio (0);
std::cin >> n;
for (int i = 1; i <= n; ++i)
std::cin >> A[i];
sort (A + 1, A + 1 + n, std::greater <int> ());
int p = 0;
while (A[p + 1] >= p + 1) ++p;
--p;
int cp = p, odd1 = 0, odd2 = 0;
while (A[p + 1] >= cp + 1) ++cp, odd1 ^= 1; cp = p;
while (A[p + 1] > cp) ++p, odd2 ^= 1;
std::cout << ((odd2 && odd1) ? "Second" : "First") << ‘\n‘;
return 0;
}
被我乱 dp 搞过去的一道题。
首先我们发现一个性质,就是我们考虑枚举这些白色球的位置,设为 \(p_1 p_2 ... p_k\),那么方案数实际上是
问题变成了怎么求这个东西。
考虑设 \(dp_{i, j}\) 为前 \(i\) 个 \(p\),\(p_i = j\) 的方案数,优化一下可以做到 \(O(n^2 k)\).
我们发现要做到比 \(O(n^2 k)\) 小,那么 \(p\) 的具体值肯定不能出现在 \(dp\) 过程中。我们发现一个关键性质,就是每一个颜色肯定是先出现白色球,再出现有颜色的,也就是说我们可以对于每一个颜色分两类考虑。
也就是说实际上你是考虑决策一坨东西的拓扑序:
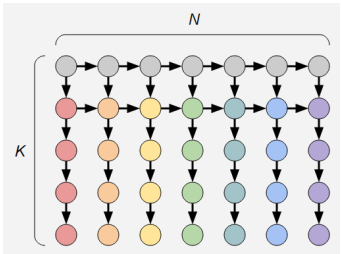
其中一个颜色的位置要一起决策。所以你就设 \(dp_{i, j}\) 表示出现了 \(i\) 个白球,\(j\) 种颜色,然后决策新出现白球还是新出现颜色即可。
我觉得贪心题的难度都很不正常啊。。。
经典的观察上界——构造上界的构造方法。本题观察到若 \(a_i \geq 1\),则上界为 \(floor(S/2)\). 构造方法如下:
for (int k = i; k < j; ++k) {
ans += a[k] / 2;
a[k] %= 2;
if (a[k] && a[k + 1]) ans++, a[k]--, a[k+1]--;
}
那么据此推理可以得到中间有 0 的情况。
我写了一个憨批做法:对每一个数进行 pollard-rho 分解,每个质因子幂次 %3,这样就可以找出唯一一种不能同时选的东西。这是一个基环树森林,选最大独立集是一个经典的 dp.
这题是一个对于出现次数很聪明的转化,就是倒推。
具体地,先用单调栈将 \(q_i\) 变成严格递增,随后考虑这样一个暴力:
把第 \(Q\) 个版本的数列设成全 \(1\),大小为 \(q_i\).
构造第 \(Q-1\) 个版本,大小为 \(q_{i-1}\) 的数列,方法:第 \(i\) 个位置是所有第 \(Q\) 个版本 \(\mod\ q_{i-1} = i\) 的下标对应的值的和。
如此往复构造第 \(Q-2\) 个版本,第 \(Q-3\) 个版本...
输出第 \(1\) 个版本。
也就是说这是一个反累计的问题,也是一种贡献法。
那么考虑 \(2\) 操作和 \(3\) 操作如何优化复杂度。假如有整除关系很好做,所有的值都是一样的,所以我们令 \(t_i\) 表示 \(i\) 版本是几倍的 \(q\) 版本,倒推即可。问题转化为如何将边角的部分也直接加到答案里。
方法是这样的。我们定义 \(f(len, w)\) 为将长度为 \(len\) 的边角料内的所有值加上 \(w\) 的操作。那么考虑找到最后一个比 \(len\) 小的长度对应的下标 \(p\)。假如找不到 \(p\),那么一定意味着原序列就比 \(len\) 长,这时候我们用一个差分数组来支持前 \(len\) 个数 \(+1\). 不然我们就考虑让那一个长度对应的 \(t\) 加上若干个整块的值,随后递归下去处理。
这样每次复杂度至少减半,加上二分复杂度是 \(Q\log^2n\). 很妙的一个题。
#include <bits/stdc++.h>
typedef long long ll;
const int AZB = 100100;
int N, Q, par[AZB];
ll q[AZB], q1[AZB], cnt, tm[AZB];
ll S[AZB];
void f (long long len, long long tms) {
int pos = std::upper_bound (q, q + cnt, len) - q; // first place > len
if (pos == 0) {
S[1] += tms;
S[len + 1] -= tms;
return ;
}
else {
tm[pos - 1] += (len / q[pos - 1]) * tms;
f (len % q[pos - 1], tms);
}
}
int main() {
std::ios::sync_with_stdio (0);
std::cin >> N >> Q;
for (int i = 1; i <= Q; ++i) std::cin >> q[i]; q[0] = N;
std::stack<int> stk;
memset (par, -1, sizeof (par));
for (int i = 0; i <= Q; ++i) {
while (!stk.empty() && q[stk.top()] >= q[i])
stk.pop();
if (stk.size()) par[i] = stk.top();
stk.push(i);
}
int cur = Q;
while (~cur) q1[cnt++] = q[cur], cur = par[cur];
std::reverse (q1, q1 + cnt);
memcpy (q, q1, sizeof (q1));
tm[cnt - 1] = 1;
for (int i = cnt - 1; i >= 1; --i) {
tm[i - 1] += (q[i] / q[i - 1]) * tm[i];
f (q[i] % q[i - 1], tm[i]);
}
S[1] += tm[0];
S[q[0] + 1] -= tm[0];
for (int i = 1; i <= N; ++i) {
S[i] += S[i - 1];
std::cout << S[i] << ‘\n‘;
}
return 0;
}
首先特判掉整个黑格子连通块都不连接边界的情况,显然可以直接快速幂。
原文:https://www.cnblogs.com/LiM-233/p/14492643.html